Основы Вакуумной Техникипроф.д.т.н. Деулин Е.АЛекция 8 Расчёт проводимости трубопроводов

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Вопросы к билетам по представленной лекции:
1.-Формулы проводимости цилиндрического трубопровода при различных режимах течения газа
2.-Связь проводимости трубопровода со степенью вакуума.
3.- Проводимость диафрагмы и проводимость трубопровода сложной формы
4.- Физические и технические основы расчёта проводимости методом Монте- Карло
5.-Методика расчёта проводимости сложного трубопровода методом Монте- Карло
6.-Преимущества расчёта проводимости методом Монте- Карло перед «геометрическими» методами расчёта по формулам проводимости

Основное уравнение ВакТехники : или
связывает параметры трёх основных компонентов вакуумной системы: быстроту действия насоса, проводимость трубопровода и быстроту откачки реципиента, поэтому расчёт проводимости трубопроводов актуален при расчёте вакуумной системы
1 – насос;
2 – вакуумопровод;
3–реципиент откачиваемый объём ).
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

Проводимость параллельно соединенных трубопроводов:
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
UΣ=U1+U2+…Ui ;
Проводимость последовательно соединенных трубопроводов:
Проводимость отверстия (диафрагмы):
S – площадь диафрагмы [м2];

1) Вязкостный (ламинарный) режим:
Формулы для расчёта проводимости цилиндрического трубопровода
d – диаметр вакуумопровода [м],
l – длина вакуумопровода [м],
P – давление [Па].
Для воздуха при t=20°C => d>10·l
2) Молекулярно-вязкостный режим:
3) Молекулярный режим:
Для воздуха при t=20°C => d>10·l
Для воздуха при t=20°C => d>10·l
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

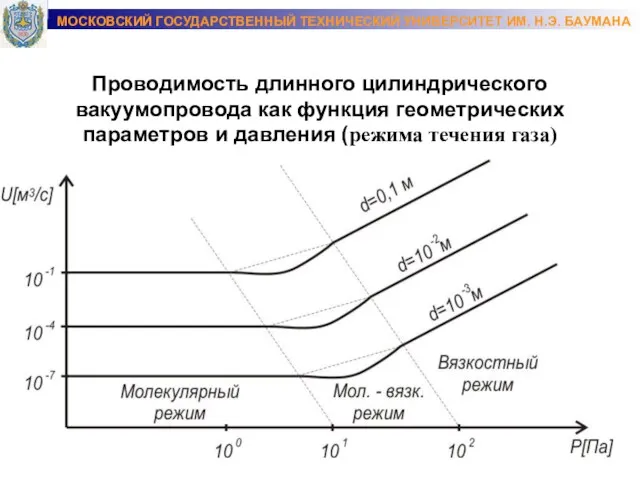
Проводимость длинного цилиндрического вакуумопровода как функция геометрических параметров и давления (режима течения газа)
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

1) Вязкостный (ламинарный) режим (низкий вакуум):
Проводимость вакуумо- провода, учитывает режим течения, характер явления переноса (вязкости) и, тем самым, степень вакуума
d – диаметр вакуумопровода [м],
l – длина вакуумопровода [м],
P – давление [Па].
Для воздуха при t=20°C => l >10· d
2) Молекулярно-вязкостный режим (средний вакуум):
3) Молекулярный режим (высокий вакуум):
Для воздуха при t=20°C => l >10· d
Для трубы:
Для воздуха при t=20°C => l >10· d
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

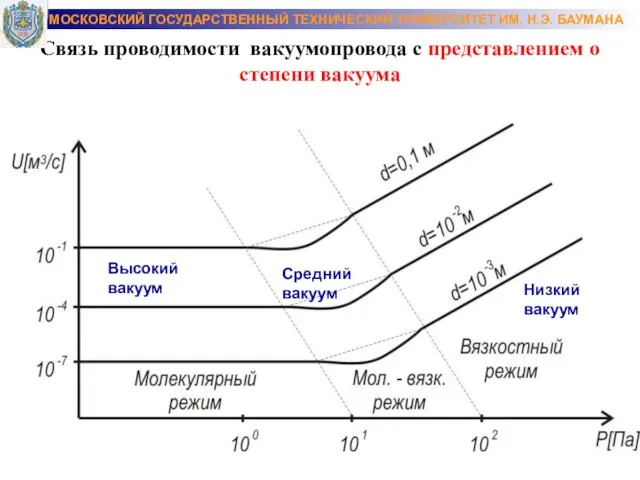
Связь проводимости вакуумопровода с представлением о степени вакуума
Низкий вакуум
Высокий вакуум
Средний вакуум
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

Формулы расчёта проводимости трубопровода сложной формы
трубопровод длинной (L>lOd) может быть представлен цилиндрической трубой постоянного диаметра его проводимость может быть определена (для воздуха М=29, Т=293 К, молекулярный режим течения газа):
, м3с-1 (1)
где:d- расчетный диаметр трубопровода окончательной откачки, м;
расчетная длина трубопровода окончательной откачки, м.
Наличие клапана или затвора с таким же диаметром прохода учиты­вается увеличением длины L на величина (2-6) dсобственно вакуумпровод окончательной откачки, который на расчетных схемах может быть представлен трубопроводом постоянного сечения, если элементы конс­трукций клапана, откачного гнезда, ловушки, золотника не диафрагмируют этот трубопровод. В общем виде суммарная проводимость трубопровода состоящего из последовательно соединенных проводимостью Ui:
м3с-1 , (2)
где: m- количество последовательно соединенных участков трубопровода, учитываемых при расчете;
Суммарная проводимость трубопровода состоящего из параллельно соединенных участков (например, в золотниковых машинах):
,3с-1 (3)
где: n- количество параллельно соединенных участков. Проводимость тонкой диафрагмы (длина L→0 определяется только ее площадью А:
где: Т- температура газа, К; М- молекулярный вес газа, Кмоль; Vi- объем газа, ударяющегося о единицу поверхности в единицу времени, Vi=ll7 м3м-2с-1 (при М = 29, Т = 293 К).
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

Расчёт проводимости трубопровода сложной формы
Проводимость трубопровода произвольной формы может быть найдена как: U=UД⋅K (4),
где:UД- проводимость входного сечения рассматриваемого трубопровода.
Чтобы рассчитать проводимость участков следующих за "диафрагмой"), необходимо ползоваться коэффициентом Клаузинга:
где:NΣ- суммарное число молекул, вошедших в трубопровод через впускное сечение;
Nобр- число "обратных" молекул, отраженных от стенок и вернув­шихся через впускное сечение.
При откачке в молекулярно-вязкостном режиме течения газа проводимость трубопровода может определяться:
UМВ=0,9UМ+UВ (5)
где:UМВ, UМ, UВ- расчетная проводимость трубопровода в молекуляр-
но-вяэкостном, молекулярном, вязкостном режимах, соответственно.
Таблицы формул для расчёта проводимости трубопроводов для газа, М=29, Т=293 К
Приведены на последующих слайдах
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Проводимость отверстия (диафрагмы) произвольной формы:
Проводимость трубопровода в виде щели
a>>b,
l- длина

Формулы расчёта проводимости трубопроводов различного сечения
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

Формулы предыдущих слайдов показывают необходимость создания универсального метода для расчёта проводимости сложных трубопроводов - метода пробных испытаний (Метода Монте- Карло)
Моделирование поведения молекул подчиняется Закону Кнудсена:
Молекулы при соударении с поверхностью задерживаются на ней на время τ, поэтому угол отражения не зависит от угла падения
В начале расчёта определяется проводимость впускной диафрагмы Uo рассчитываеиого нами трубопровода
где А [см2] – площадь диафрагмы
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

Формулы предыдущих слайдов показывают необходимость создания универсального метода для расчёта проводимости сложных трубопроводов - метода пробных испытаний (Метода Монте- Карло)
Моделирование поведения молекул подчиняется Закону Кнудсена:
Молекулы при соударении с поверхностью задерживаются на ней на время τ, поэтому угол отражения не зависящий от угла падения является случайной величиной, подчиняющейся указанному «Кнудсеновскому» закону распределения и определяемой генератором случайных чисел
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Пример чисел, выдаваемых генератором случайных чисел, подчиняющихся «Кнудсеновскому» закону распределения, и характеризующих угол отражения от 0 до 180 0 с округлением значения до 100 (т.е. чисел от 1 до 17 с функцией распределения по закону cos φ )

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Виды угловых распределений молекул по скоростям:
Слева- равномерное распределение; Справа- распределение Кнудсена

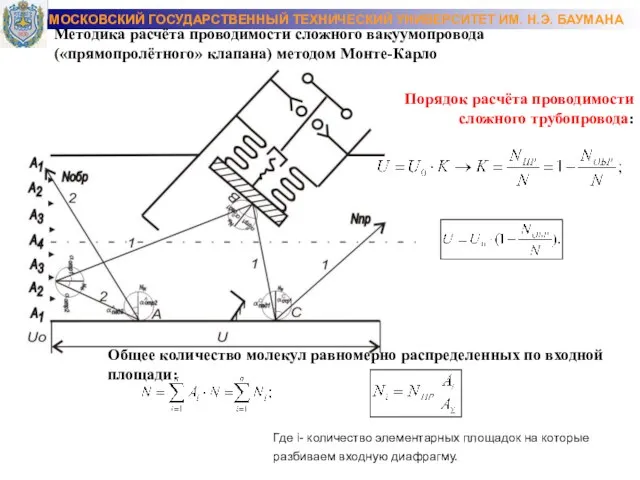
Методика расчёта проводимости сложного вакуумопровода («прямопролётного» клапана) методом Монте-Карло
Порядок расчёта проводимости сложного трубопровода:
Общее количество молекул равномерно распределенных по входной площади:
Где i- количество элементарных площадок на которые разбиваем входную диафрагму.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Вид в разрезе «углового» клапана КРУТ DY=40 Рассмотрим расчёт проводимости этого клапана методом МК в плоской ( 2D ) системе координат

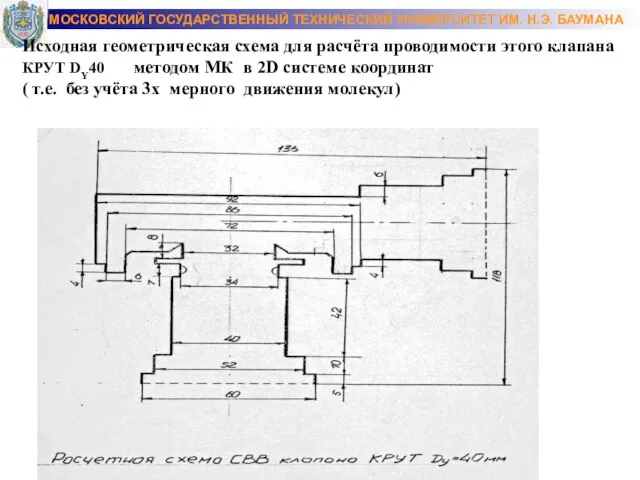
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Исходная геометрическая схема для расчёта проводимости этого клапана КРУТ DY40 методом МК в 2D системе координат
( т.е. без учёта 3х мерного движения молекул)

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Схема, поясняющая необходимость изменения размеров на плоском чертеже (2D схема) для учёта 3х координатного движения молекул.
Истинное соотношение размеров
Соотношение размеров при графическом расчете на плоскости в 2D системе с учётом 3х координатного движения молекул
Пример распределения чисел от 1 до 17 с функцией распределения по закону cos φ выдаваемых генератором случайных чисел (см. следующие слайды)

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Геометрическая схема клапана КРУТ DY40 для расчёта его проводимости методом МК в 2D системе координат (На базе исходной с учётом 3х мерного движения молекул) 1 запуск 10 молекул
«Впускная диафрагма» клапана

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Геометрическая схема клапана КРУТ DY40 для расчёта его проводимости методом МК в 2D системе координат (На базе исходной с учётом 3х мерного движения молекул) 2 запуск 10 молекул
«Впускная диафрагма» клапана

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Геометрическая схема клапана КРУТ DY40 для расчёта его проводимости методом МК в 2D системе координат (На базе исходной с учётом 3х мерного движения молекул) 3 запуск 30 молекул
«обратные» моле кулы

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Геометрическая схема клапана КРУТ DY40 для расчёта его проводимости методом МК в 2D системе координат (На базе исходной с учётом 3х мерного движения молекул) 4 запуск 10 молекул
Видны траектории «прямых» и «обратных» молекул

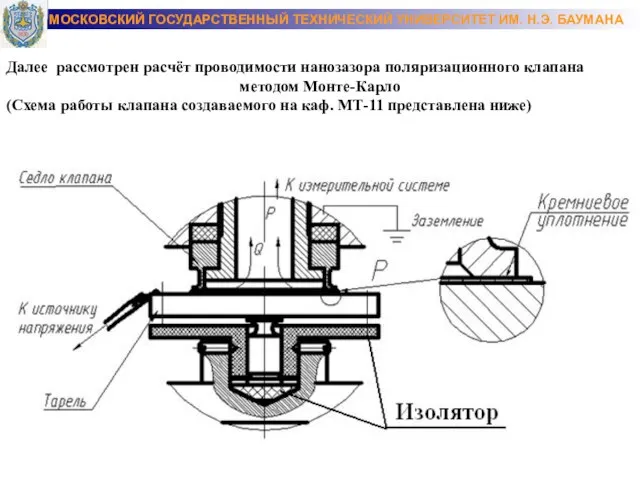
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Далее рассмотрен расчёт проводимости нанозазора поляризационного клапана
методом Монте-Карло
(Схема работы клапана создаваемого на каф. МТ-11 представлена ниже)

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Пример расчёта проводимости нанозазора поляризационного клапана методом Монте-Карло На рис. представлены элементы модели, использованные для расчёта суммарной проводимости плоского уплотнения:
слева- сегмент кольца, покрытый сканами; справа-трубопровод, эквивалентный сегменту кольца (сектор кольца уплотнения, с наложенными на него сканами)

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Элементы процесса расчёта проводимости нанозазора поляризационного клапана методом Монте-Карло
В вакуумной технике для расчета проводимости сложных разветвленных трубопроводов часто пользуются методом электрических аналогий. При последовательном соединении n элементов вакуумной системы с известными проводимостями Ui общая проводимость системы (1)
При параллельном соединении n элементов вакуумной системы ее общая проводимость U равна сумме проводимостей всех элементов . (2)
Для n последовательно соединенных элементов вакуумной системы формула принимает вид: (3)
где
P0i – вероятность прохождения молекулы через i-й элемент вакуумной системы (коэффициент Клаузинга);
P0 – суммарная вероятность прохождения частицы через n последовательно соединенных элементов вакуумной системы

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Вид сканов поверхностей элементов уплотнения клапана :
а) кремния; б) алюминия; в) меди

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Компьютерная реконструкция нанозазора в уплотнении
между контактирующими поверхностями по сканам поверхностей :
тарели (нижняя поверхность)
и седла (верхняя поверхность).

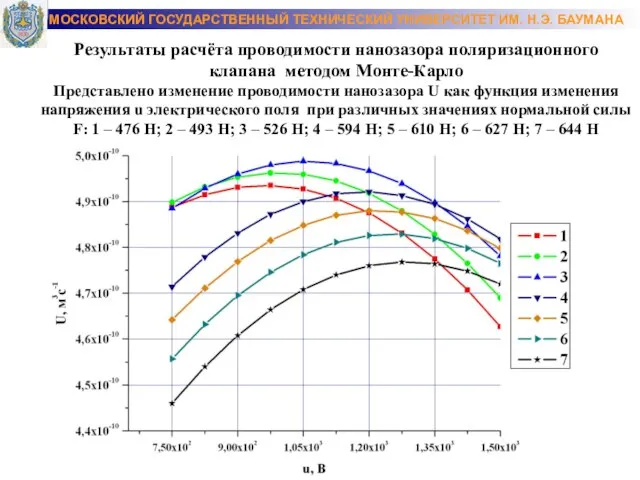
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Н.Э. БАУМАНА
Результаты расчёта проводимости нанозазора поляризационного клапана методом Монте-Карло
Представлено изменение проводимости нанозазора U как функция изменения напряжения u электрического поля при различных значениях нормальной силы F: 1 – 476 Н; 2 – 493 Н; 3 – 526 Н; 4 – 594 Н; 5 – 610 Н; 6 – 627 Н; 7 – 644 Н