Отчет о выполнении работы

Цель работы:
применение методов обработки экспериментальных данных для изучения статистических закономерностей при измерении интенсивности радиационного фона.

В работе используются:
счетчик Гейгера-Мюллера (СТС-6),
блок питания,
компьютер с интерфейсом связи со счетчиков.

1. В результате демонстрационного эксперимента убеждаемся, что при увеличении числа измерений:
измеряемая величина флуктуирует;
флуктуации среднего значения измеряемой величины уменьшаются, и среднее значение выходит на постоянную величину;
флуктуации величины погрешности отдельного измерения уменьшаются, и погрешность отдельного измерения выходит на постоянную величину;
флуктуации величины погрешности среднего значения уменьшаются, а сама величина убывает.
Ход работы

2. Переходим к основному эксперименту: измерение плотности потока космического излучения за 10 секунд. На компьютере проведем обработку, аналогичную сделанной в демонстрационном эксперименте. Результаты приведены в таблицах 1 и 2.

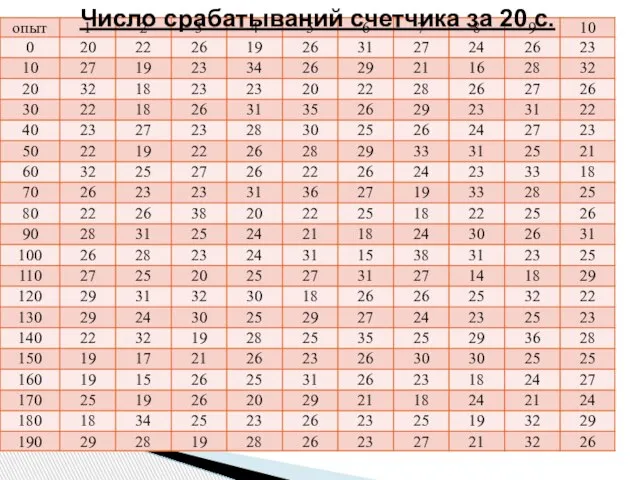
Число срабатываний счетчика за 20 с.

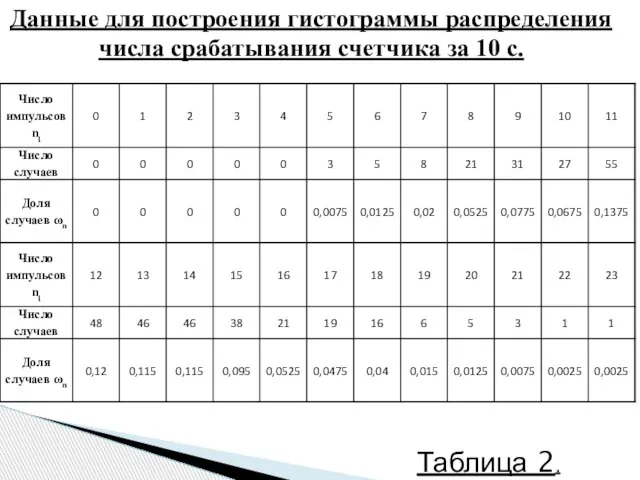
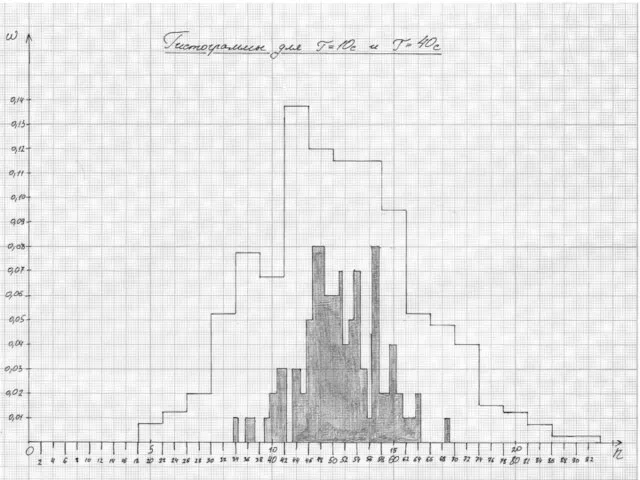
Данные для построения гистограммы распределения числа срабатывания счетчика за 10 с.
Таблица 2.

3. Разбиваем результаты измерений из таблицы 1 в порядке их получения на группы по 2, что соответствует проведению N2=100 измерений числа частиц за интервал времени, равный 40 с. Результаты сведем в таблицу 3.

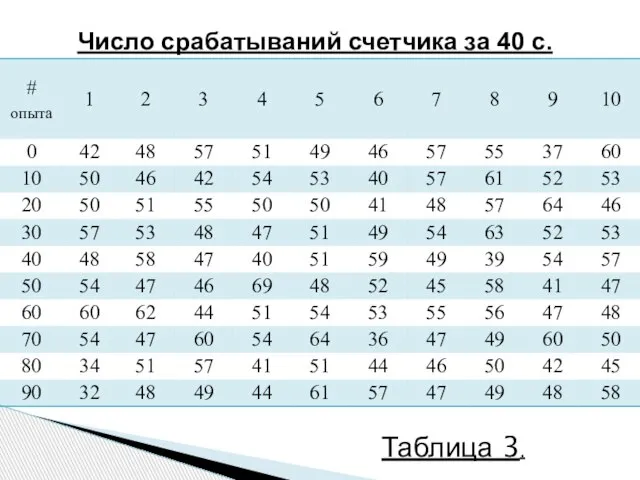
Число срабатываний счетчика за 40 с.
Таблица 3.

4. Представим результаты последнего распределения в виде, удобном для построения гистограммы (таблица 4). Гистограммы распределений среднего числа отсчетов за 10 и 40 с строим на одном графике. При этом для второго распределения цену деления по оси абсцисс увеличиваем в 4 раза, чтобы положения максимумов распределений совпадали.

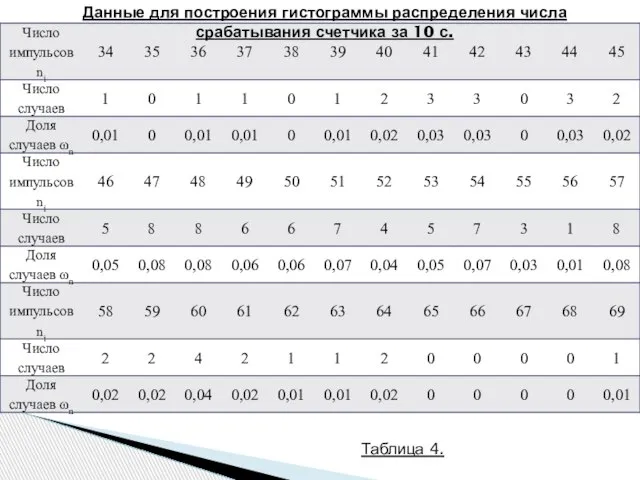
Данные для построения гистограммы распределения числа срабатывания счетчика за 10 с.
Таблица 4.

5. Определим среднее число срабатываний счетчика за 10 с:

6. Найдем среднеквадратичную ошибку отдельного измерения:

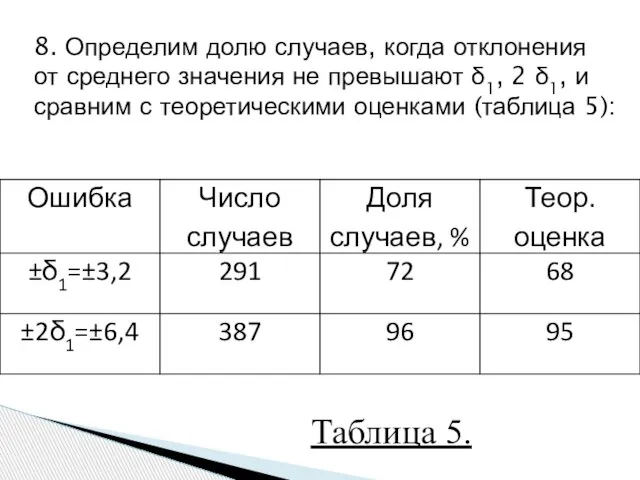
7. Убедимся в справедливости формулы 5:

8. Определим долю случаев, когда отклонения от среднего значения не превышают δ1, 2 δ1, и сравним с теоретическими оценками (таблица 5):
Таблица 5.

9. Используя формулу (3), определим среднее число импульсов счетчика за 40 с:

10. Найдем среднеквадратичную ошибку отдельного измерения по формуле 4:

11. Убедимся в справедливости формулы (5):

12. Сравним среднеквадратичные ошибки отдельных измерений для двух распределений:

Легко видеть, что хотя абсолютное значение δ во втором распределении больше, чем в первом (7,13>3,2), относительная полуширина второго распределения меньше:
Это следует также из рис.2 (гистограмма).

13. Определим стандартную ошибку величины n1 и относительную ошибку нахождения n1 для N=400 измерений по 10 с. По формуле (6):

Найдем относительную ошибку двумя вариантами:

Окончательный результат:

14. Определим стандартную ошибку для величины n2 и относительную ошибку нахождения n2 для N2=100 измерений по 40 с:

Относительная ошибка двумя вариантами:

Окончательный результат:

Вывод: в ходе лабораторной работы были применены методы обработки экспериментальных данных для изучения статистических закономерностей при измерении интенсивности радиационного фона. Были получены следующие результаты: