Содержание
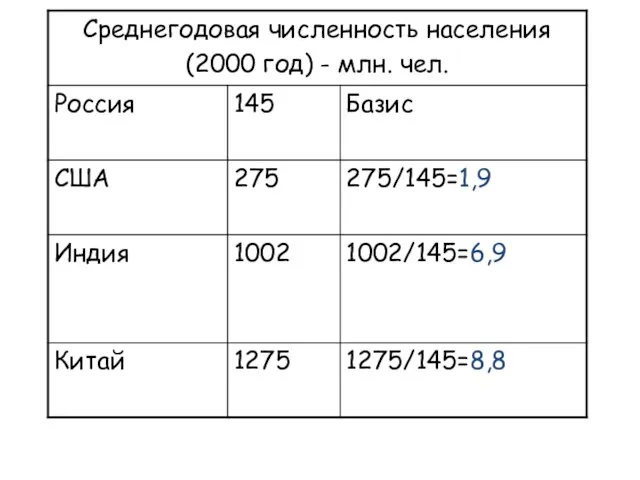
- 2. Для характеристики массовых явлений статистика использует статистические величины (показатели): абсолютные, относительные, средние.
- 3. Абсолютные величины всегда имеют свою единицу измерения (размерность), присущую изучаемому явлению. Каждая абсолютная величин имеют единицу
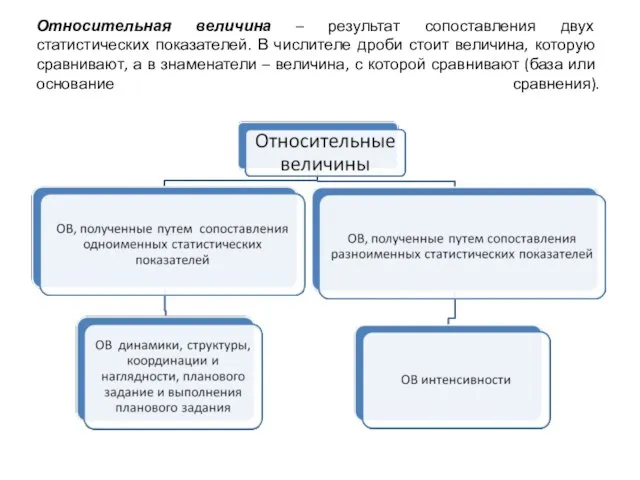
- 4. Относительная величина – результат сопоставления двух статистических показателей. В числителе дроби стоит величина, которую сравнивают, а
- 5. Относительный показатель
- 6. Цепной относительный показатель – если база сравнения переменная Базисный относительный показатель – если база сравнения постоянная
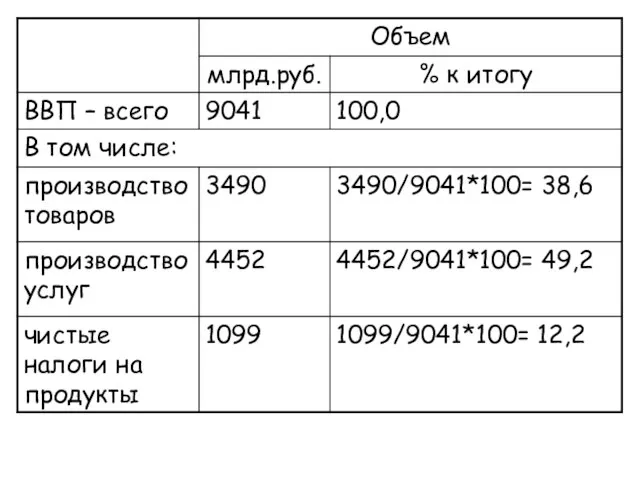
- 7. Относительный показатель обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин и определяется как
- 8. Относительный показатель динамики – темп роста Характеризует изменение уровня развития какого-либо явления во времени
- 9. Пример Реализация хлопчатобумажных тканей секцией универмага составила в январе 3956 тыс. руб., в феврале – 4200
- 10. Темпы роста: Базисные (база - уровень реализации в январе) ОВДф/я = 4200 * 100% =106,3% 3950
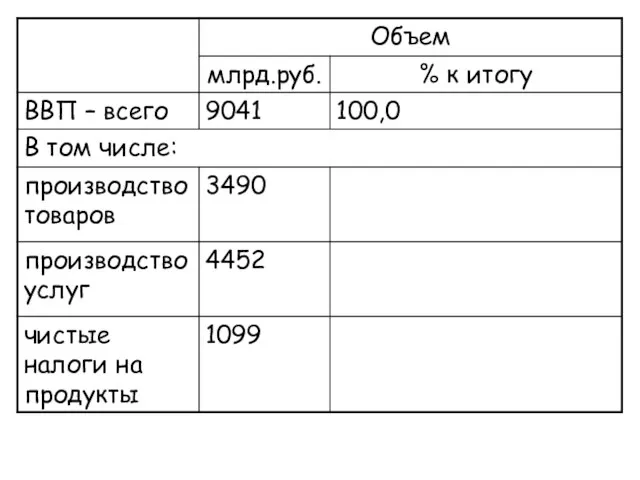
- 11. Задание Валовый внутренний продукт в России составил: 2005 г. - 21,6 трлн. руб., 2006 – 26,9
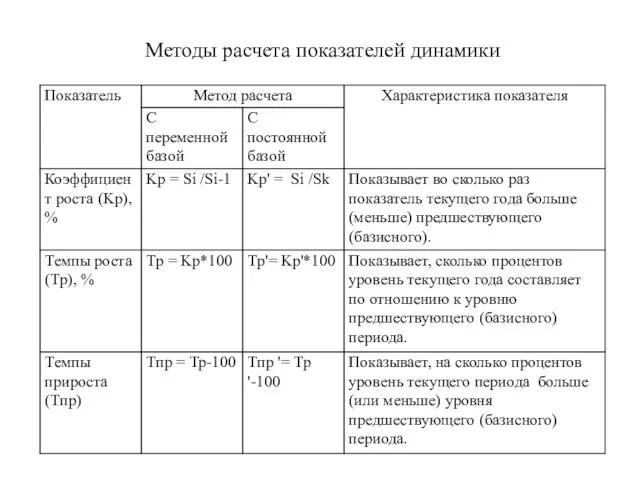
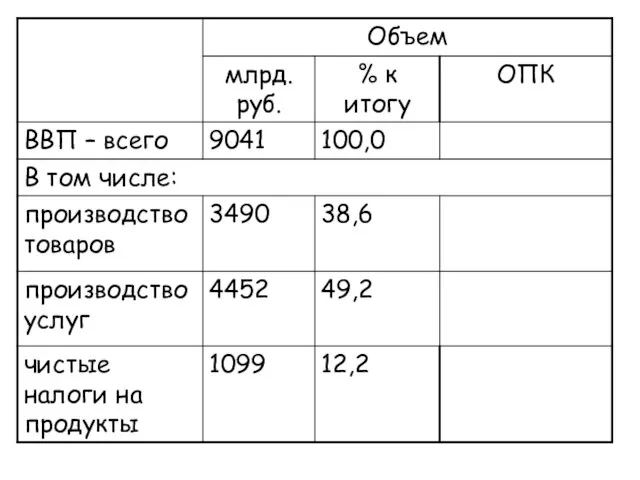
- 12. Методы расчета показателей динамики
- 13. Относительный показатель выполнения плана и планового задания ; . ОПП*ОПРП=ОПД относительные показатели плана относительные показатели реализации
- 14. Оборот торговой фирмы в 2002 г. составил 2,0 млн. руб. На 2003 год запланировано достичь оборота
- 15. Относительные величины структуры Характеризуют доли, удельные веса составных элементов в общем итоге
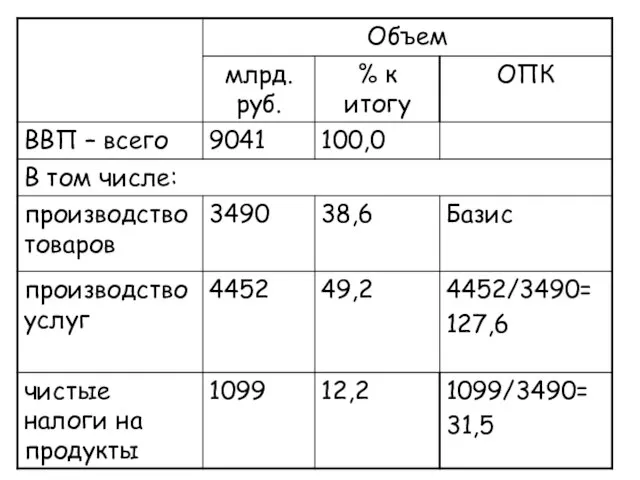
- 18. Относительный показатель координации Характеризует отношение частей данной совокупности к одной из них, принятой за базу сравнения
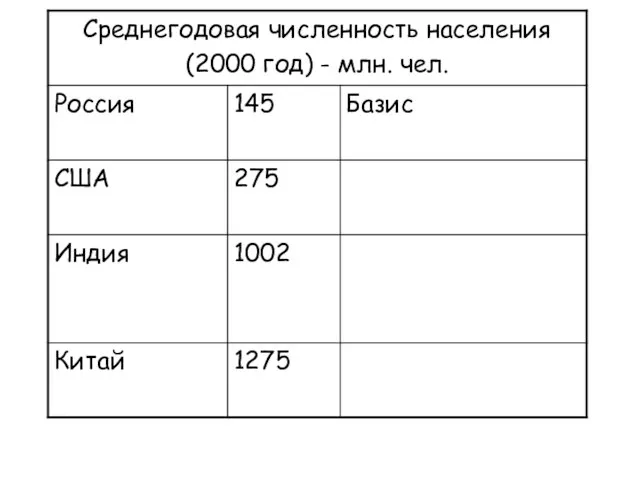
- 21. Относительный показатель сравнения Характеризует сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду
- 24. Относительный показатель интенсивности Характеризует степень распределения или развития данного явления в той или иной среде
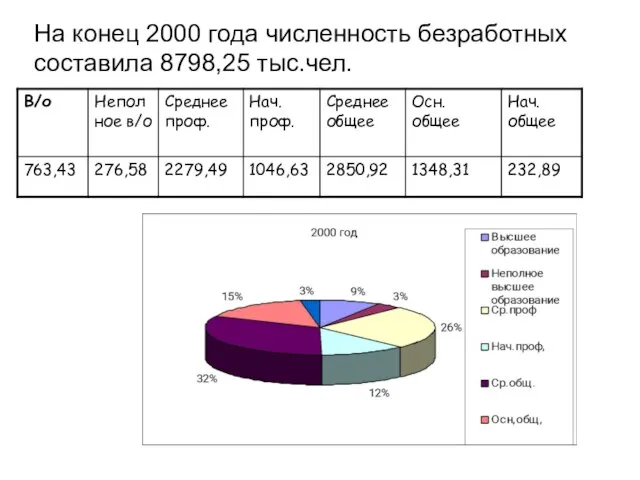
- 25. На конец 2000 года численность безработных составила 8798,25 тыс.чел.
- 26. Средний показатель обобщающий показатель, характеризующий типический уровень явления
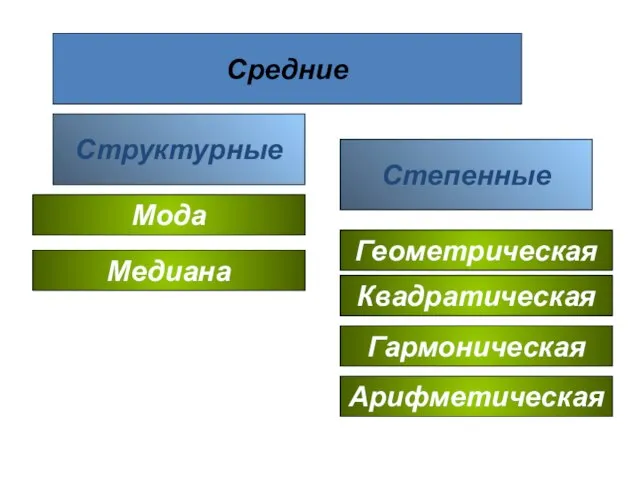
- 27. Средние Степенные Структурные Арифметическая Гармоническая Геометрическая Мода Квадратическая Медиана
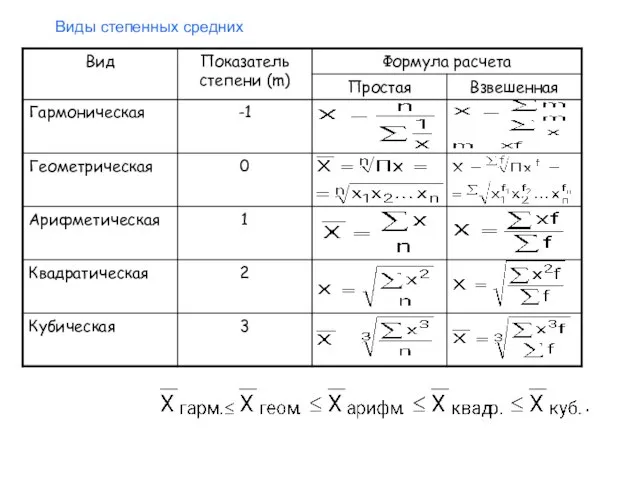
- 28. Степенные средние Простая средняя где Xi - варианта (значение) осредняемого признака; m - показатель степени средней;
- 29. Виды степенных средних
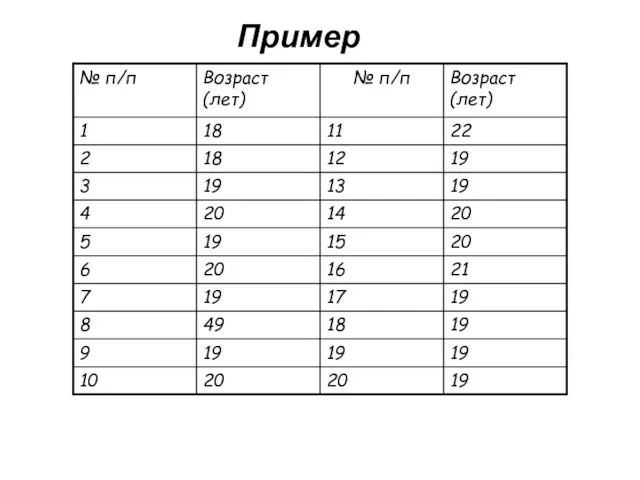
- 30. Пример
- 31. Средний возраст Простая средняя Взвешенная средняя
- 32. Структурные средние Мода наиболее часто повторяющееся значения признака где ХMo - нижнее значение модального интервала; mMo
- 33. Структурные средние Медиана величина признака, которая делит упорядоченную последовательность его значений на две равные по численности
- 34. Показатели вариации: частотные показатели; показатели распределения – структурные средние; показатели степени вариации; показатели формы распределения.
- 35. Частотные показатели вариации абсолютная численность i-той группы – частота fi относительная частота – частость di кумулятивная
- 36. Показатели вариации:
- 37. Показатели вариации:
- 38. Дисперсия: Дисперсия постоянной величины равна 0. Если все значения вариантов признака X уменьшить на постоянную величину
- 39. Показатели относительного рассеивания :
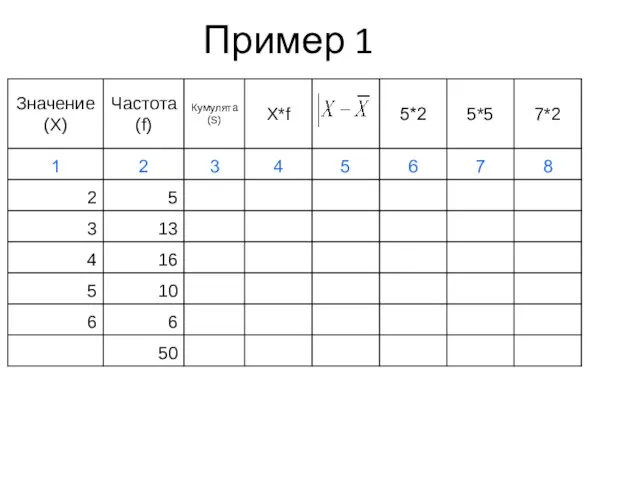
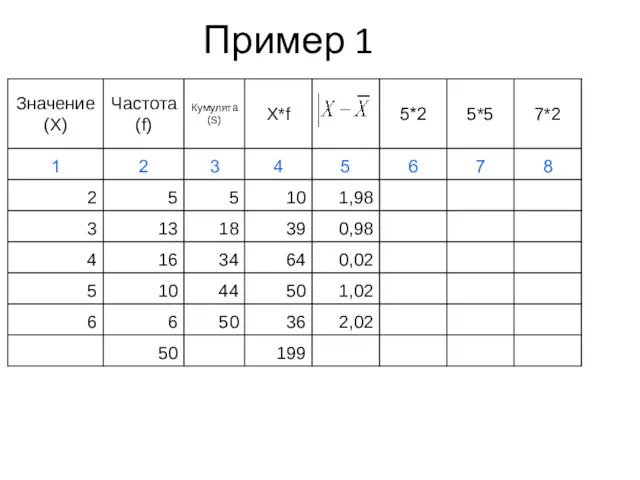
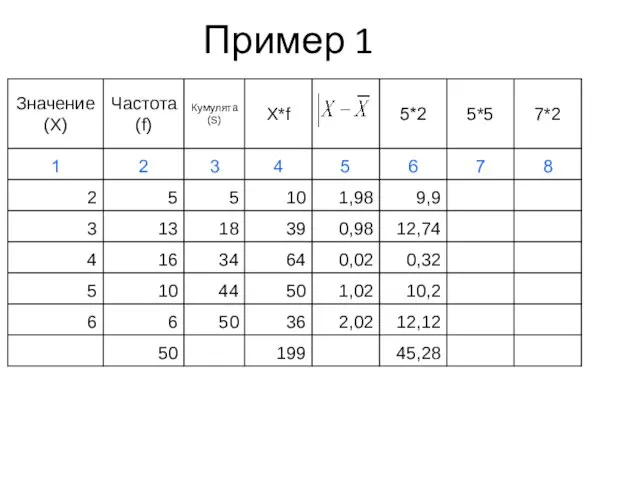
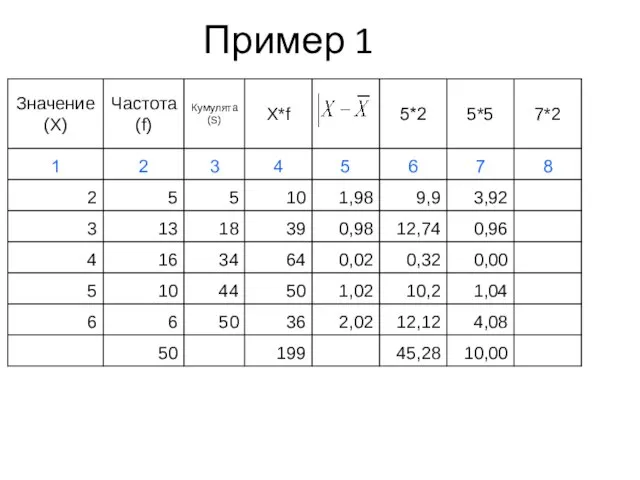
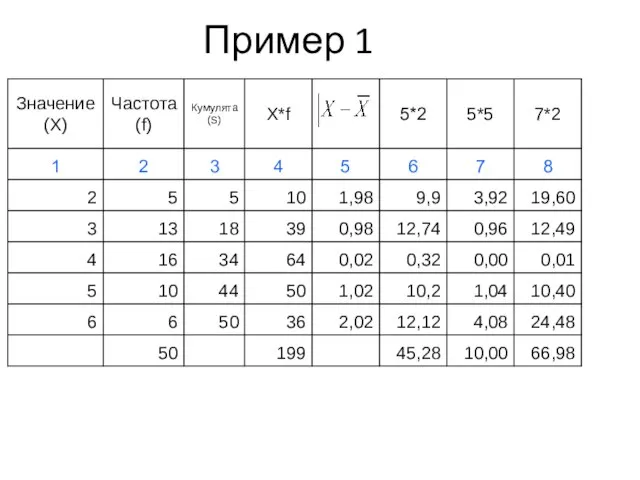
- 40. Пример 1
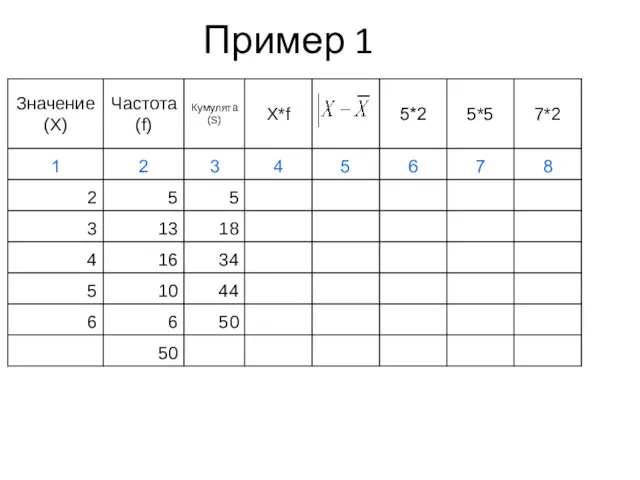
- 41. Пример 1
- 42. Пример 1
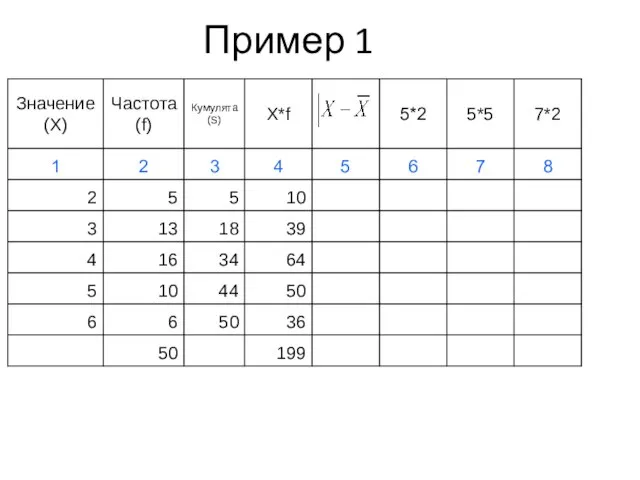
- 43. Пример 1
- 44. Пример 1
- 45. Пример 1
- 46. Пример 1
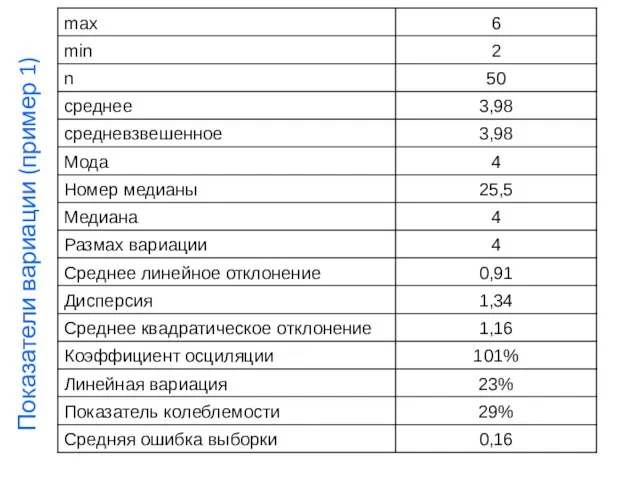
- 47. Показатели вариации (пример 1)
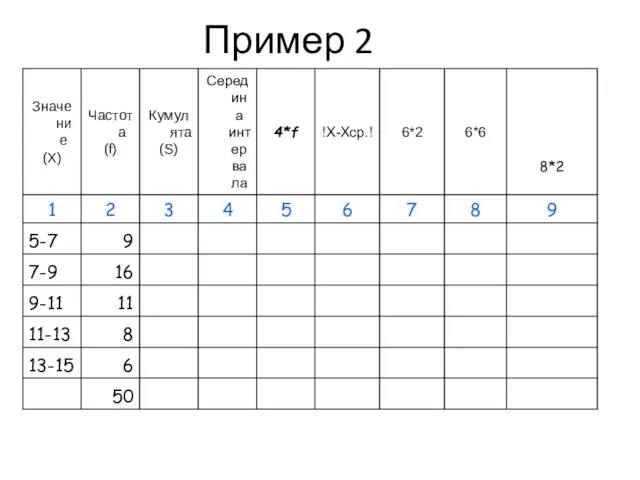
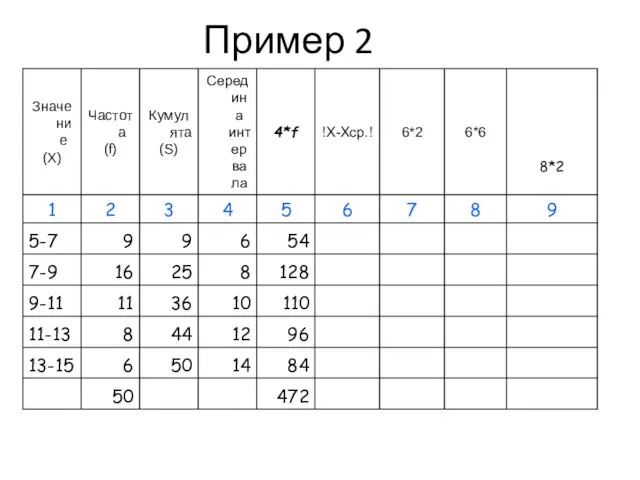
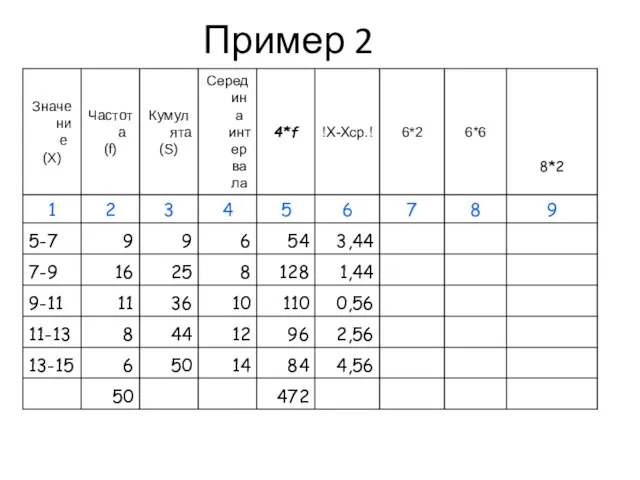
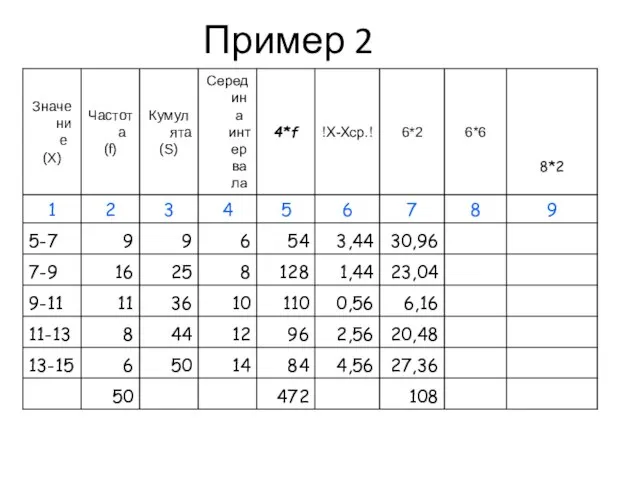
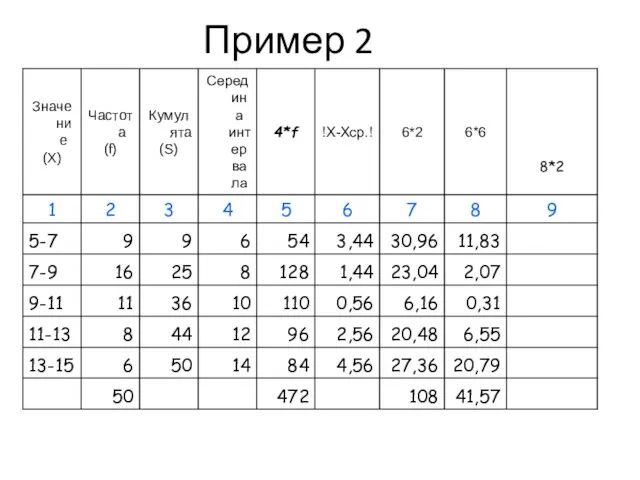
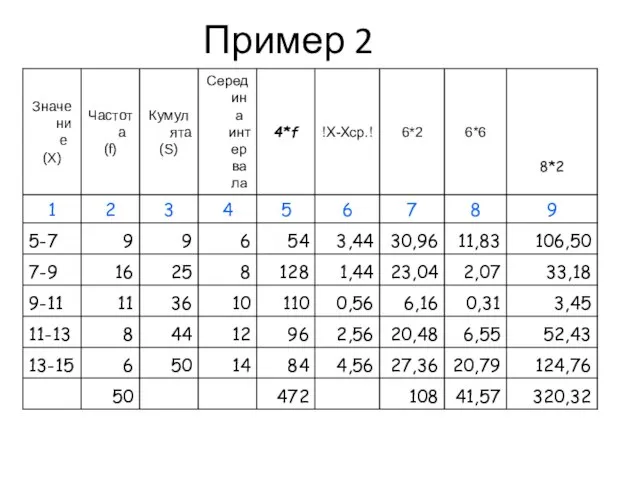
- 48. Пример 2
- 49. Пример 2
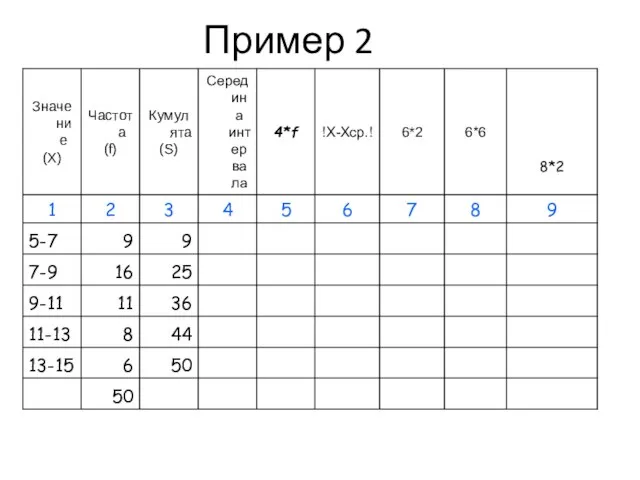
- 50. Пример 2
- 51. Пример 2
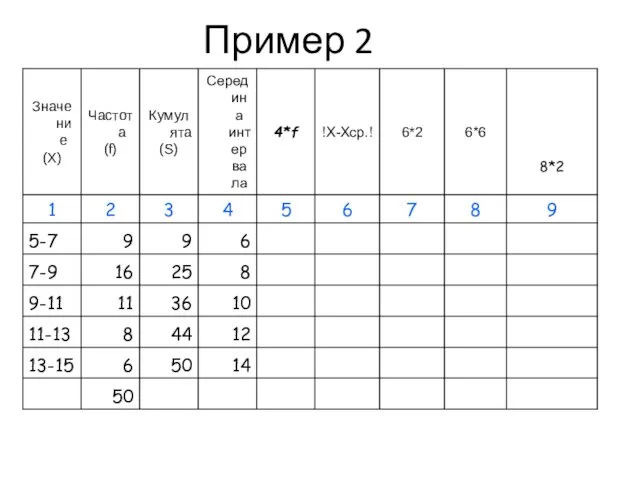
- 52. Пример 2
- 53. Пример 2
- 54. Пример 2
- 55. Пример 2
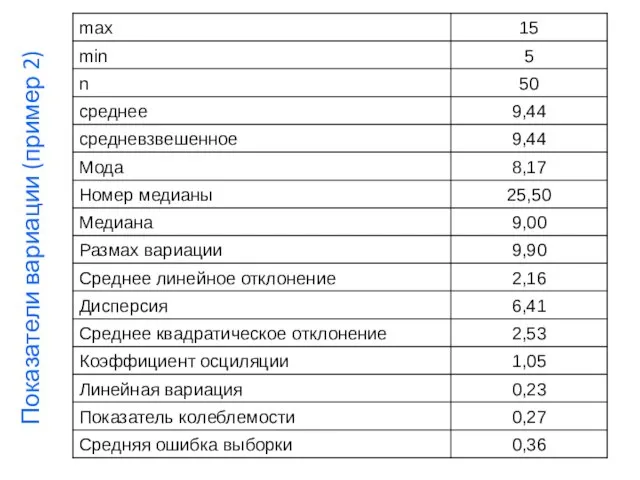
- 56. Показатели вариации (пример 2)
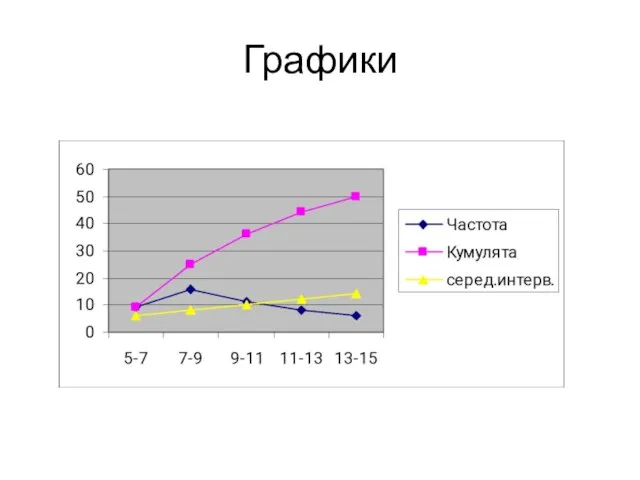
- 57. Графики
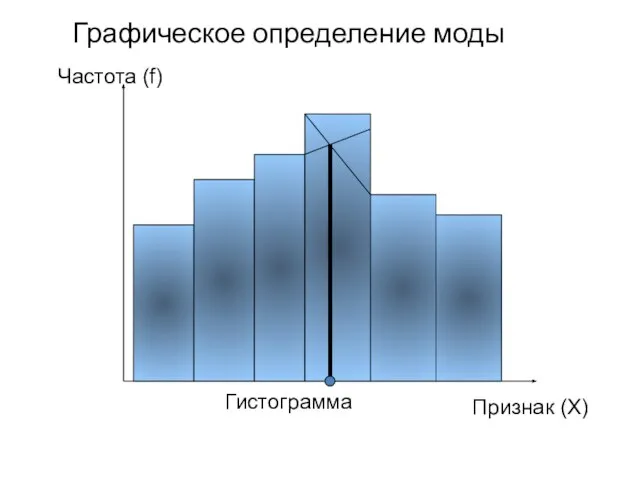
- 58. Графическое определение моды Гистограмма Частота (f) Признак (X)
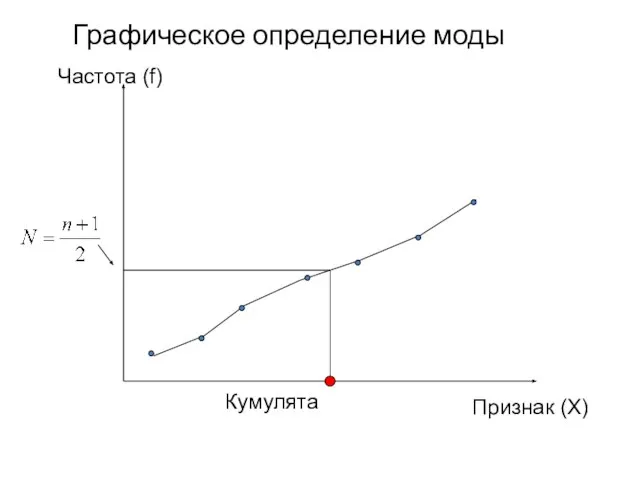
- 59. Графическое определение моды Кумулята Частота (f) Признак (X)
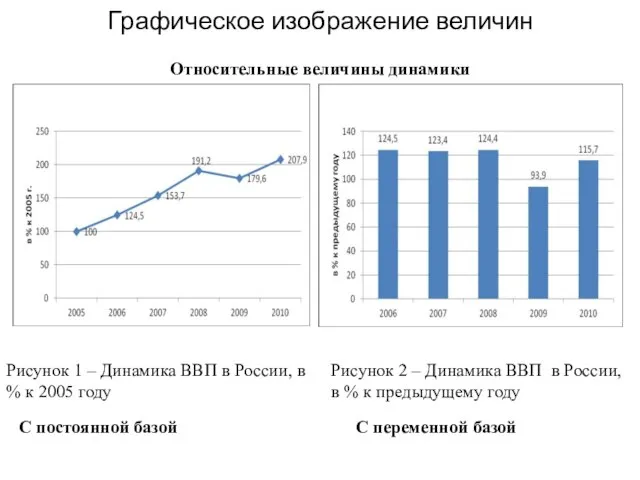
- 60. Графическое изображение величин Рисунок 1 – Динамика ВВП в России, в % к 2005 году Рисунок
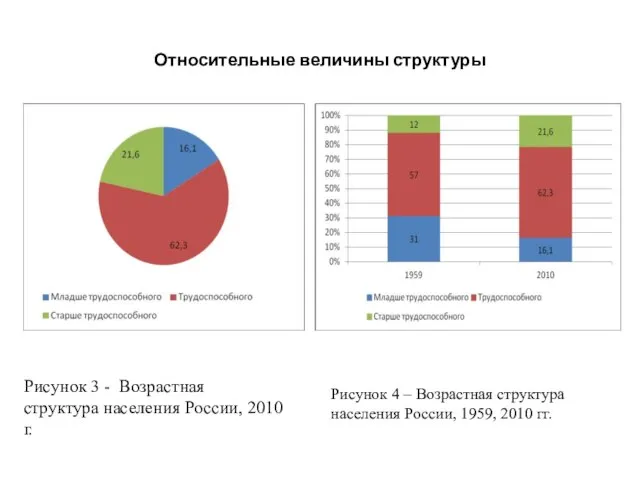
- 61. Относительные величины структуры Рисунок 3 - Возрастная структура населения России, 2010 г. Рисунок 4 – Возрастная
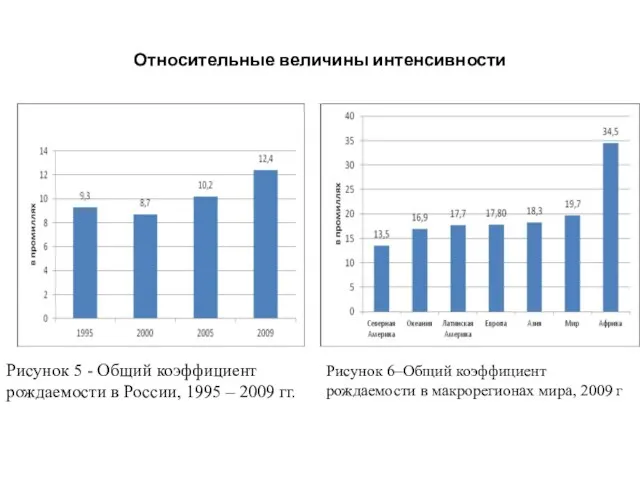
- 62. Относительные величины интенсивности Рисунок 5 - Общий коэффициент рождаемости в России, 1995 – 2009 гг. Рисунок
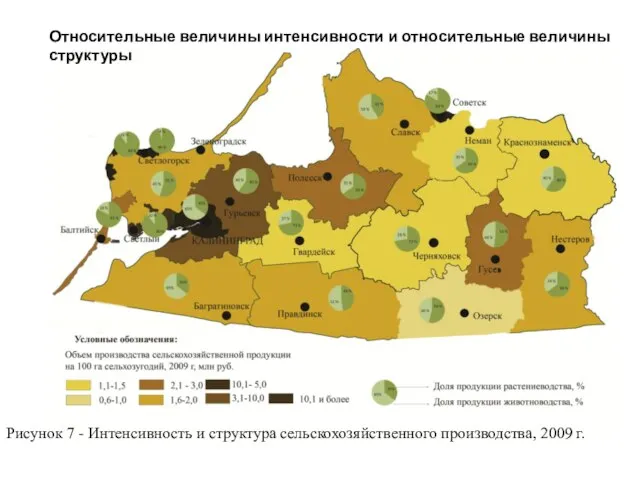
- 63. Рисунок 7 - Интенсивность и структура сельскохозяйственного производства, 2009 г. Относительные величины интенсивности и относительные величины
- 65. Скачать презентацию

























 ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ
ПЕДАГОГИКА ПОДДЕРЖКИ РЕБЕНКА И ПРОЦЕСС ЕГО РАЗВИТИЯ В СИСТЕМЕ ЛИЧНОСТНО-ОРИЕНТИРОВАННОГО ВОСПИТАНИЯ Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары
Лас су желісі. Канализация құбырлары мен коллекторларының кесінді қималары Career in law abroad
Career in law abroad  ТЕМА : ГЛАГОЛ
ТЕМА : ГЛАГОЛ Технология обработки сырья и приготовления блюд
Технология обработки сырья и приготовления блюд Prezentare (2)
Prezentare (2) Смертная карта
Смертная карта  Центр независимых судебных экспертиз ТЕХЭКО
Центр независимых судебных экспертиз ТЕХЭКО Изложение Птицы говорят спасибо
Изложение Птицы говорят спасибо Классификация стиральных порошков
Классификация стиральных порошков Утомление при физической и умственной работе восстановление
Утомление при физической и умственной работе восстановление Презентация на тему МАТЕМАТИКА 1 КЛАСС
Презентация на тему МАТЕМАТИКА 1 КЛАСС  Презентация на тему Загадочная Намибия Племя Химба
Презентация на тему Загадочная Намибия Племя Химба  Слайд 1
Слайд 1 Правила делового этикета: как не ударить в грязь лицом
Правила делового этикета: как не ударить в грязь лицом Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь
Проект воздухоразделительной установки №7 в условиях АО Уральская Сталь «Рио+20», устойчивое развитие и торговля
«Рио+20», устойчивое развитие и торговля Поэтам и писателям. Нургисаева Айжана
Поэтам и писателям. Нургисаева Айжана Проверка парных согласных и безударных гласных в корне слова
Проверка парных согласных и безударных гласных в корне слова Картины художников-передвижников
Картины художников-передвижников Информационные системы
Информационные системы Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ?
Проведение сертификационных испытаний на отсутствие НДВ. Можно ли найти НДВ? Инфекция мочевыводящих путей у беременных
Инфекция мочевыводящих путей у беременных Политический режим
Политический режим Московский Городской Педагогический УниверситетФакультет специальной педагогики
Московский Городской Педагогический УниверситетФакультет специальной педагогики Базиликовый соус Суго
Базиликовый соус Суго Семинар заместителей директоров по учебно-воспитательной работе:
Семинар заместителей директоров по учебно-воспитательной работе: История школьного портфеля
История школьного портфеля