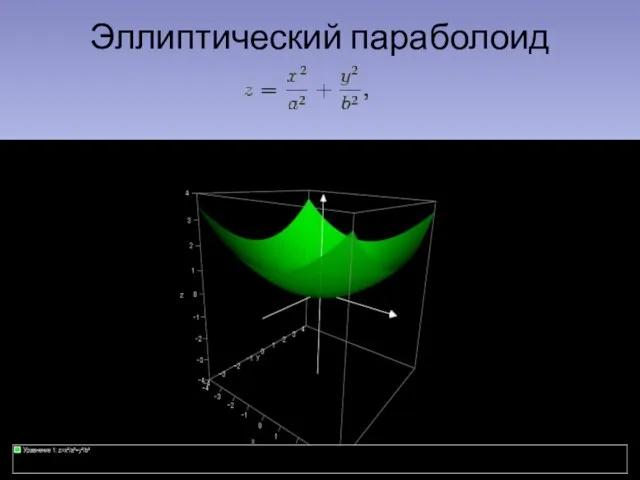
плоскостями, параллельными плоскости xOy: z = h, получаем кривые второго порядка гиперболического типа. Это либо гипербола (при |h| > 0), либо пара пересекающихся прямых (при h = 0). Таким образом, по форме гиперболический параболоид напоминает седло, эту поверхность часто называют седловой.
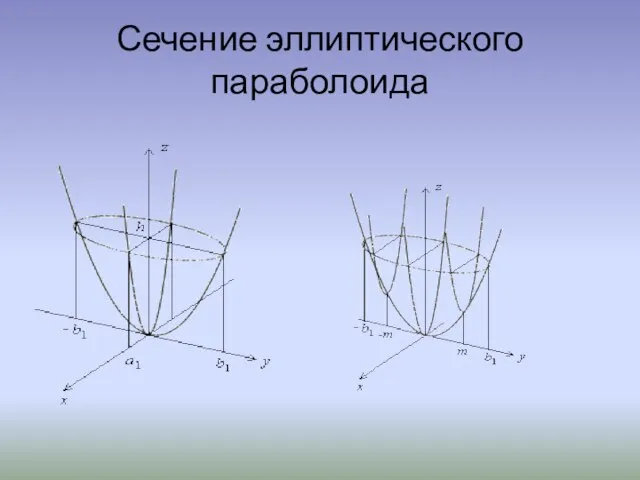
Если рассмотреть сечение гиперболического параболоида координатными плоскостями xOz: y = 0 и yOz: x = 0, и плоскостями, им параллельными (x = h1, y = h2), то в сечении получаются параболы. Например, сечение гиперболического параболоида плоскостью x = h1 задается системой уравнений
откуда при подстановке второго уравнения в первое последовательно получаем:
и уравнение параболы
.







 Грабарь Игорь Эммануилович
Грабарь Игорь Эммануилович Помоги Маше сделать покупки
Помоги Маше сделать покупки Читающий Арбат
Читающий Арбат Русский иконостас. Из цикла интерактивных лекций
Русский иконостас. Из цикла интерактивных лекций Архитектура забвения
Архитектура забвения Заблуждения о ценах
Заблуждения о ценах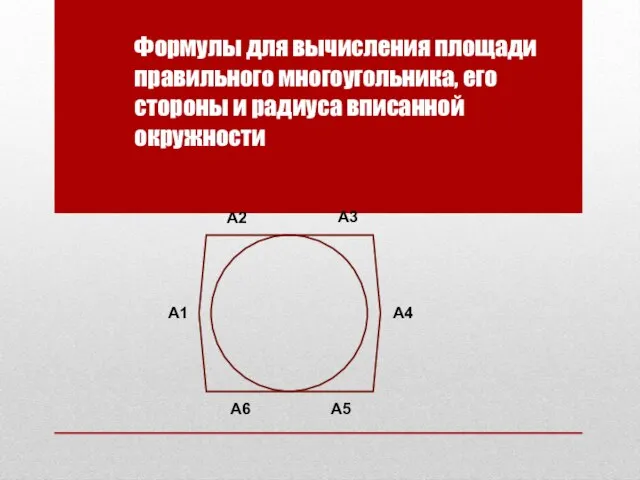 Формулы для площади стороны и радиуса
Формулы для площади стороны и радиуса Теплоэлектростанция
Теплоэлектростанция Наркотики -
Наркотики - Трудоголизм
Трудоголизм Обобщение и систематизация знаний о бессоюзных сложных предложениях
Обобщение и систематизация знаний о бессоюзных сложных предложениях Бой у мыса Акций
Бой у мыса Акций APM Mechanic
APM Mechanic Оперный жанр в творчестве композиторов XIX века. Джузеппе Верди
Оперный жанр в творчестве композиторов XIX века. Джузеппе Верди Проблемы развития инклюзивного образования детей дошкольного возраста с ограниченными возможностями здоровья в УР
Проблемы развития инклюзивного образования детей дошкольного возраста с ограниченными возможностями здоровья в УР Сущность и структура морали
Сущность и структура морали Татар теле дәресләрендә
Татар теле дәресләрендә Интерактивная дорожная экскурсия Фантомомания по маршруту Тверь - Москва - Тверь
Интерактивная дорожная экскурсия Фантомомания по маршруту Тверь - Москва - Тверь 1. Передача изготовленной продукции перевозчику для доставке потребителю или непосредственно потребителю в месте изготовления
1. Передача изготовленной продукции перевозчику для доставке потребителю или непосредственно потребителю в месте изготовления THE THEORY OF THE SIMPLE
THE THEORY OF THE SIMPLE "Требования к светоотражающей маркировке и задним опознавательным знакам в правилах ЕЭК ООН и Техническом регламенте о безопасн
"Требования к светоотражающей маркировке и задним опознавательным знакам в правилах ЕЭК ООН и Техническом регламенте о безопасн Растровая и векторная графика
Растровая и векторная графика Зонирование образовательного процесса: - зона двигательной активности - естественно научная зона - географическая зона
Зонирование образовательного процесса: - зона двигательной активности - естественно научная зона - географическая зона М.В.Ломоносов - первый историограф российского народа
М.В.Ломоносов - первый историограф российского народа Благопожелание к природеБлагопожелание к реке
Благопожелание к природеБлагопожелание к реке Трудовой распорядок. Дисциплина труда
Трудовой распорядок. Дисциплина труда Презентация на тему Биогеоценоз луга
Презентация на тему Биогеоценоз луга