Содержание
- 2. Параллельные прямые
- 3. Определение. Две прямые называются параллельными, если они не пересекаются. а b аIIb
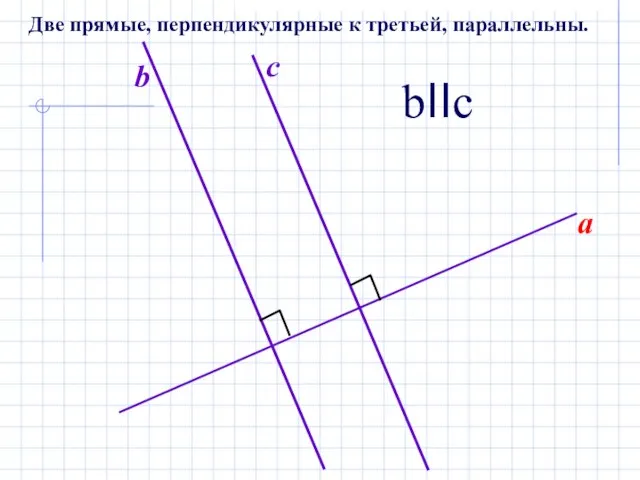
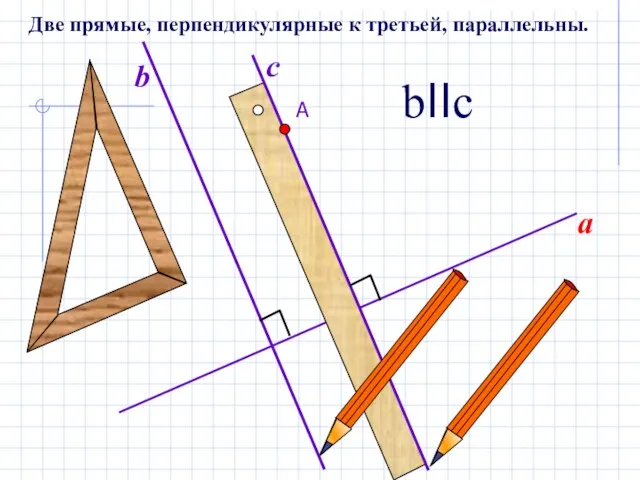
- 5. a b c bIIc Две прямые, перпендикулярные к третьей, параллельны.
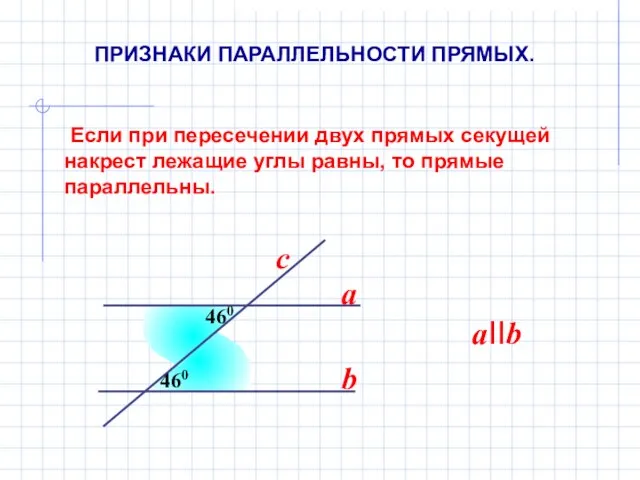
- 6. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 460 460 a
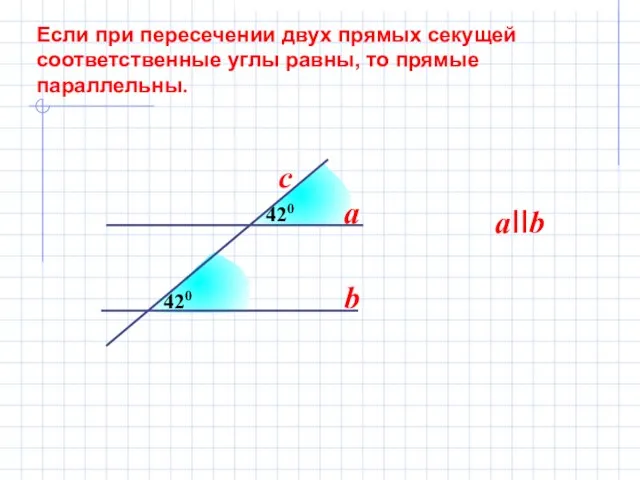
- 7. 420 Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 420 a b
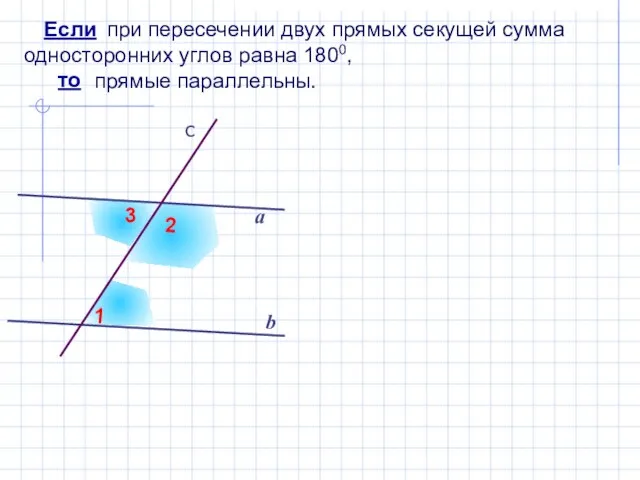
- 8. при пересечении двух прямых секущей сумма односторонних углов равна 1800, прямые параллельны. b а Если то
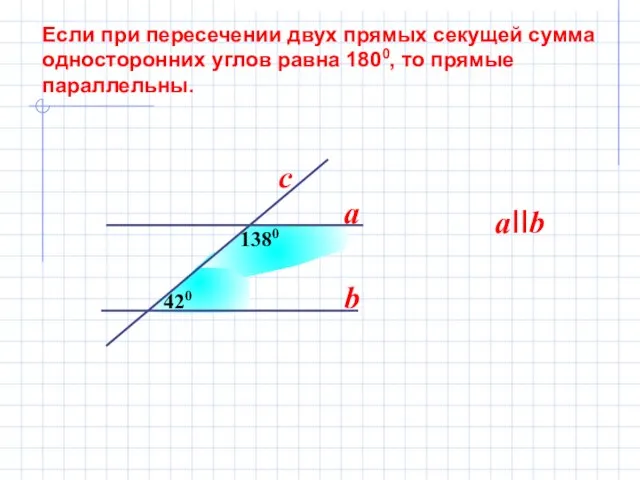
- 9. Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны. 420 1380
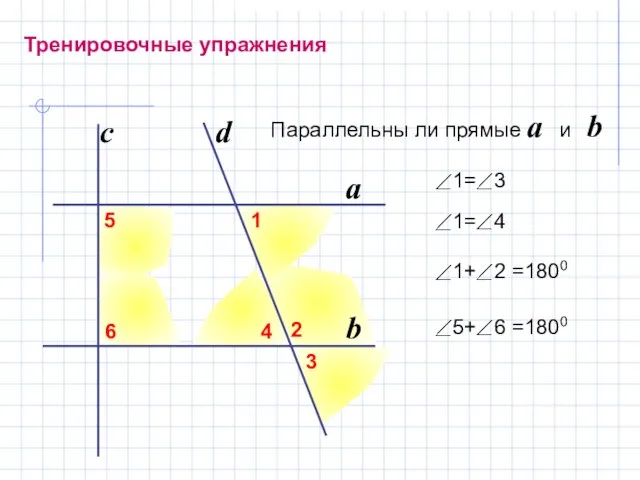
- 10. Тренировочные упражнения Параллельны ли прямые a и b b a d c 1 3 2 4
- 11. А a b c bIIc Две прямые, перпендикулярные к третьей, параллельны.
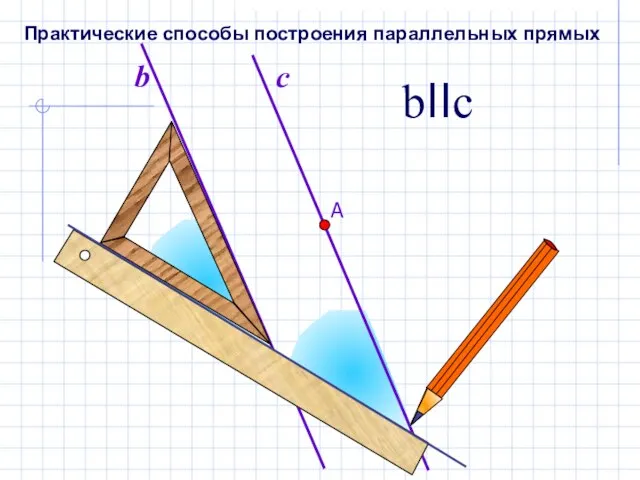
- 12. b bIIc Практические способы построения параллельных прямых
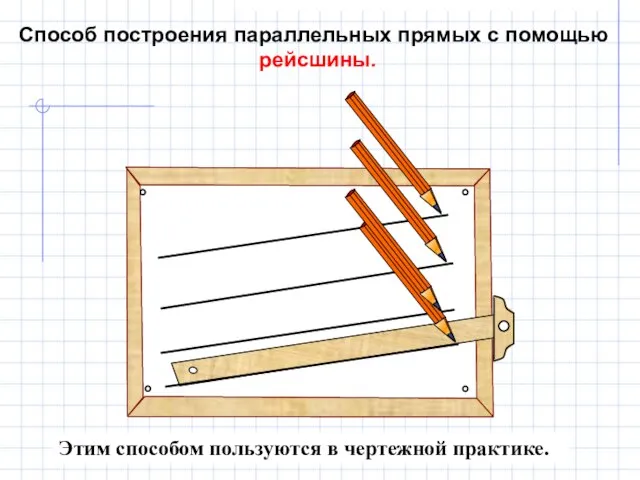
- 13. Этим способом пользуются в чертежной практике. Способ построения параллельных прямых с помощью рейсшины.
- 14. Параллельность прямой с плоскостью
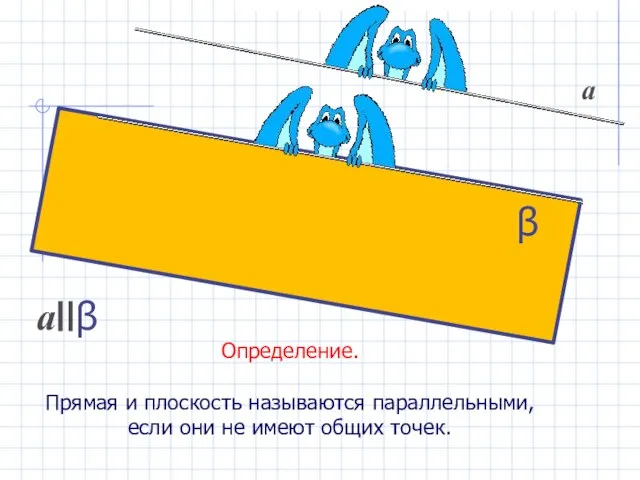
- 15. Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек. аIIβ а β
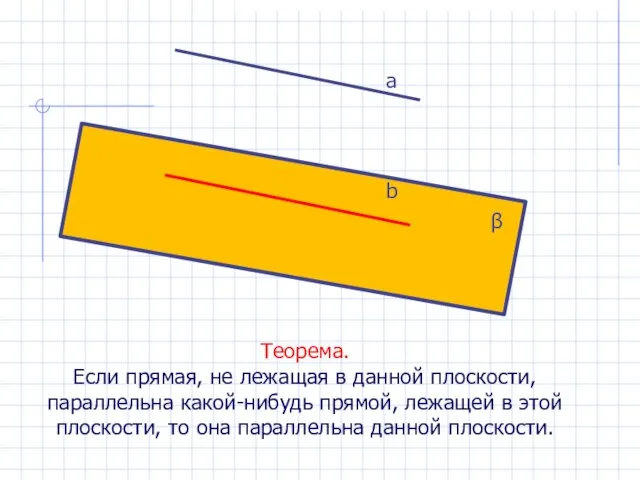
- 16. Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то
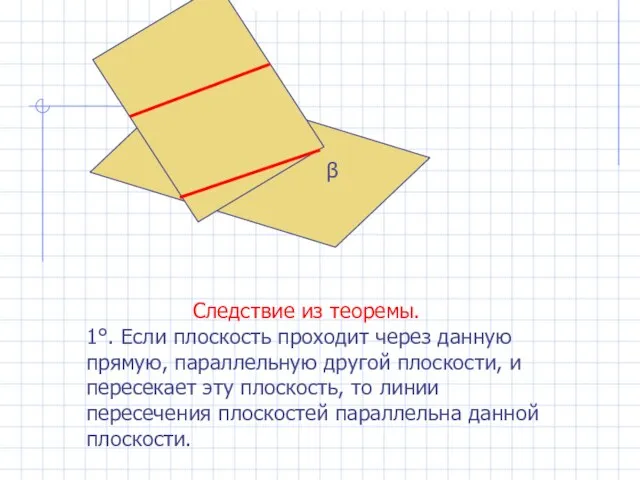
- 17. Следствие из теоремы. 1°. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту
- 18. Следствие из теоремы. 2°. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая
- 19. Параллельность плоскостей
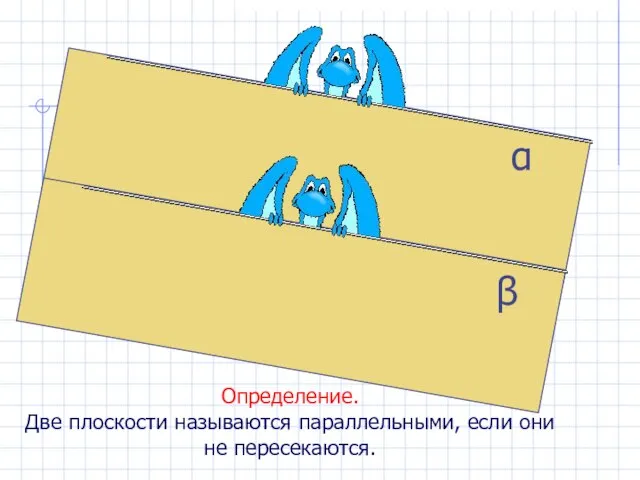
- 20. β α Определение. Две плоскости называются параллельными, если они не пересекаются.
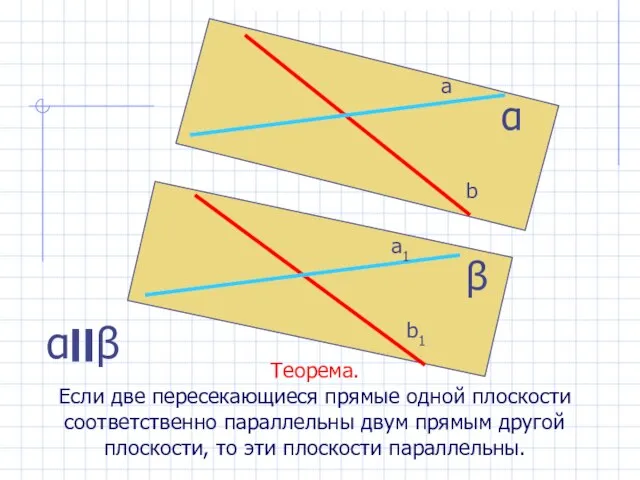
- 21. Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости
- 22. Свойства параллельных плоскостей
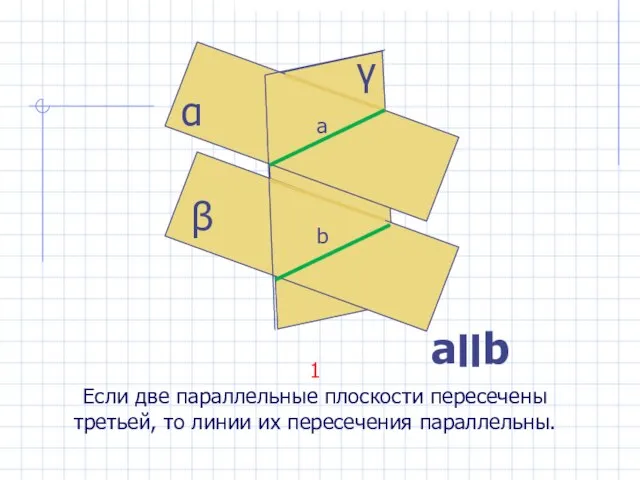
- 23. 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. α β γ a
- 25. Скачать презентацию







 Международное сотрудничество в области сертификации. Схемы сертификации. Добровольная и обязательная сертификация. Сделали: Тор
Международное сотрудничество в области сертификации. Схемы сертификации. Добровольная и обязательная сертификация. Сделали: Тор Международный день без интернета
Международный день без интернета Разделенный город как крайняя форма сегрегации городского пространства
Разделенный город как крайняя форма сегрегации городского пространства Японский виски
Японский виски Тема урока: «Прямоугольник и квадрат»
Тема урока: «Прямоугольник и квадрат» Гражданское общество и правовое государство
Гражданское общество и правовое государство Эллинистические государства в IV-IIв. до н.э. Эллинистическая культура
Эллинистические государства в IV-IIв. до н.э. Эллинистическая культура Hungry Frog
Hungry Frog Анонимные Наркоманы
Анонимные Наркоманы ТЕМА УРОКА:
ТЕМА УРОКА: Русский язык
Русский язык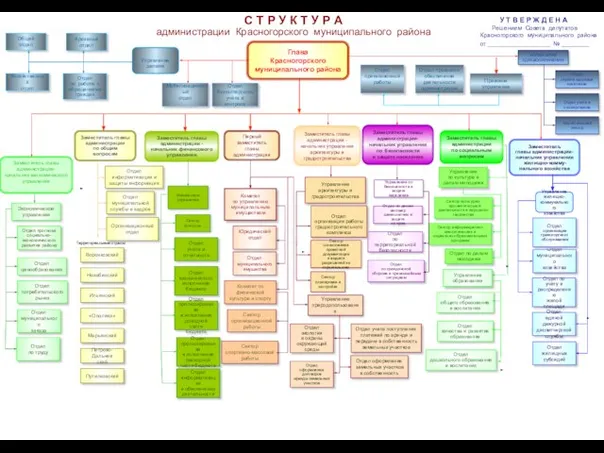 С Т Р У К Т У Р А администрации Красногорского муниципального района
С Т Р У К Т У Р А администрации Красногорского муниципального района Презентация на тему Историко-культурные объекты, сформированные на территории средневекового Тараза Южного Казахстана
Презентация на тему Историко-культурные объекты, сформированные на территории средневекового Тараза Южного Казахстана Финансовая математика
Финансовая математика Реновация промышленных зданий
Реновация промышленных зданий Как менялась этика на протяжении веков
Как менялась этика на протяжении веков Классный час «Жизнь – это…»
Классный час «Жизнь – это…» Sale 30% Bestia
Sale 30% Bestia Presentation Title
Presentation Title  Продажа мобильного ПО своими руками
Продажа мобильного ПО своими руками Государственная (итоговая) аттестация выпускников 9-х классов
Государственная (итоговая) аттестация выпускников 9-х классов география
география Зеленый Меморандум СБ. Кейс 2
Зеленый Меморандум СБ. Кейс 2 Крещенские вечера
Крещенские вечера Институты и субинституты финансового права
Институты и субинституты финансового права Презентацию подготовил ученик 3 «А» класса ГОУ средней общеобразовательной школы № 511 Добролюбов Егор Учитель: Ваниосова Н.В.
Презентацию подготовил ученик 3 «А» класса ГОУ средней общеобразовательной школы № 511 Добролюбов Егор Учитель: Ваниосова Н.В. Приметы и суеверия. Les superstitions et les présages
Приметы и суеверия. Les superstitions et les présages Способы завязывания платков
Способы завязывания платков