Слайд 2Паркетом будем называть такое покрытие плоскости правильными многоугольниками, при котором два многоугольника
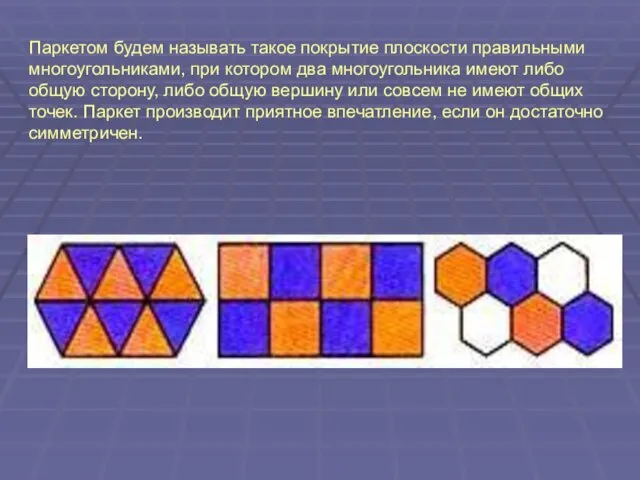
имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек. Паркет производит приятное впечатление, если он достаточно симметричен.
Слайд 3 Паркет называется правильным, если его можно наложить на самого
себя так, что

любая заданная его вершин наложится на любую другую
заданную его вершину. Существует конечное число правильных паркетов. В вершине паркета может сходиться не более шести и не менее трех многоугольников.
Паркеты с тремя многоугольниками в вершине
Слайд 4Паркеты с тремя многоугольниками в вершине
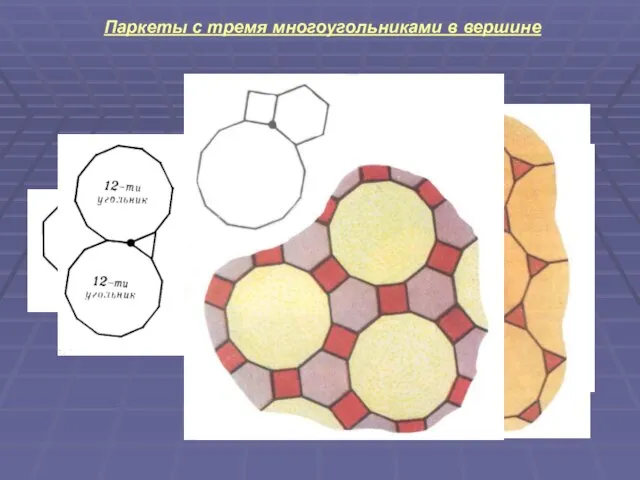
Слайд 5Паркеты с четырьмя многоугольниками в вершине
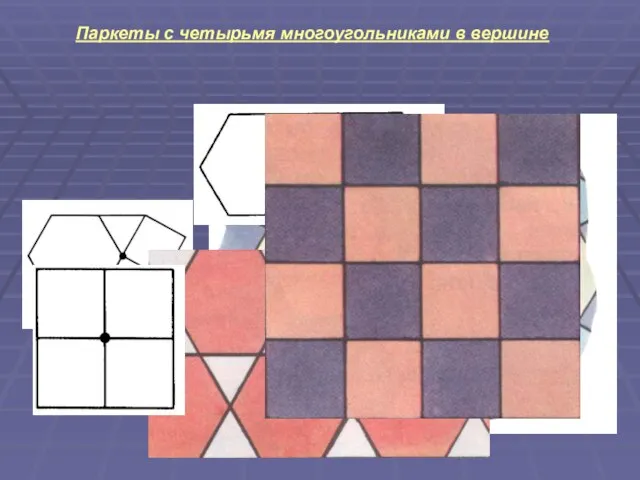
Слайд 6Паркеты с пятью многоугольниками в вершине
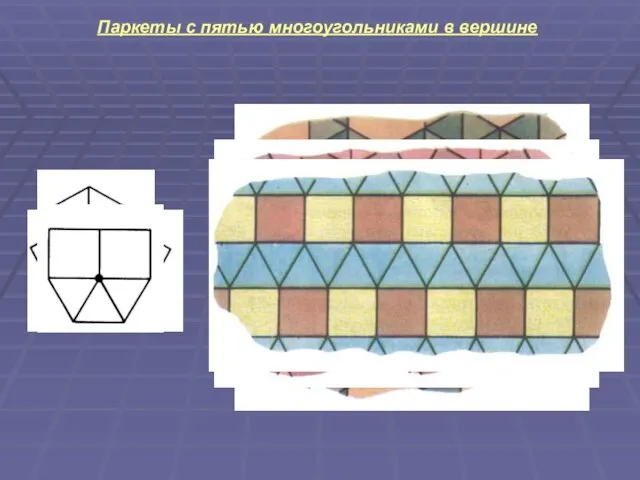
Слайд 7Паркеты с шестью многоугольниками в вершине
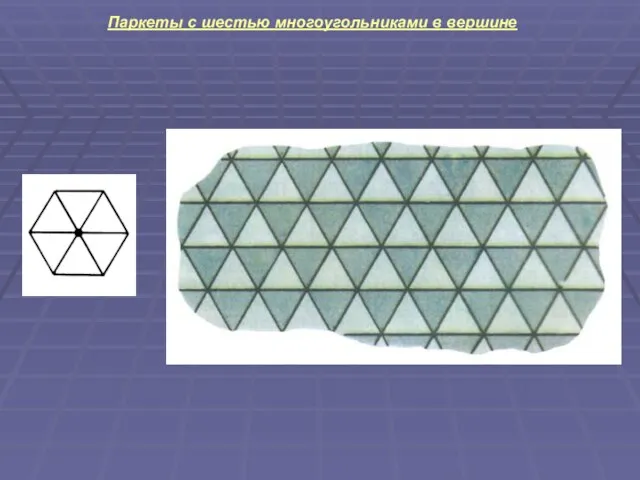
Слайд 8 Теперь займемся заполнением плоскости неправильными одинаковыми многоугольниками. Четырехугольником произвольной формы можно

заполнить всю плоскость без пробелов и наложений.
Слайд 9Отметим, что четырехугольник может быть и невыпуклым.

Слайд 10Рассматривают и другое обобщение — паркеты из копий произвольного многоугольника, правильные «по

граням».Число таких паркетов — 46. Многоугольники, которые могут быть плитками в этих паркетах, называются планигонами. Любой шестиугольник, противоположные стороны которого равны и параллельны – планигон.
Слайд 12Существуют и интересные непериодические замощения плоскости. Долгое время предполагали, что не существует
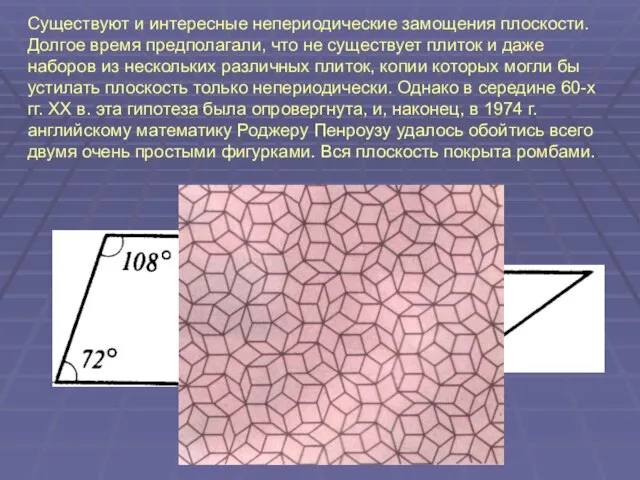
плиток и даже наборов из нескольких различных плиток, копии которых могли бы устилать плоскость только непериодически. Однако в середине 60-х гг. XX в. эта гипотеза была опровергнута, и, наконец, в 1974 г. английскому математику Роджеру Пенроузу удалось обойтись всего двумя очень простыми фигурками. Вся плоскость покрыта ромбами.
Слайд 13Это другое квазипериодическое замощение плоскости, построенное Пенроузом. Вся плоскость покрыта четырьмя многоугольниками

специального вида. Это звезда, ромб, правильный пятиугольник и «бумажный кораблик».
Слайд 14Очень красивое спиральное замощение плоскости девятиугольниками, придуманное в 1936 г. немецким математиком

X. Фодербергом. Оно составлено из большого числа конгруэнтальных девятиугольников. Оказывается конфигурация может быть продолжена до бесконечности; при этом девятиугольники продолжают разворачиваться по « двойной спирали » и заполняют всю плоскость (без пробелов и наложений друг на друга).
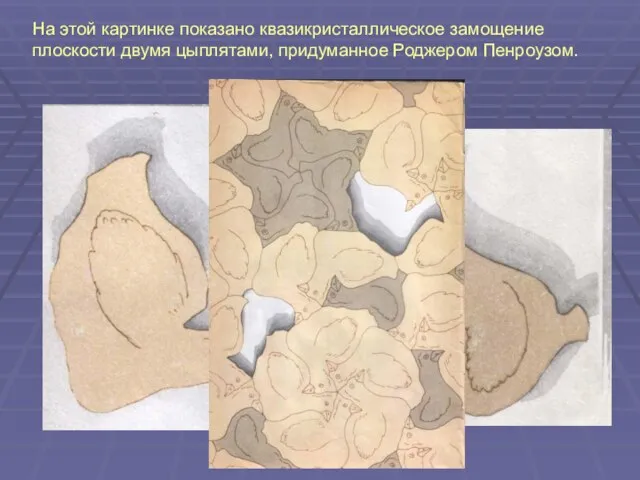
Слайд 15На этой картинке показано квазикристаллическое замощение плоскости двумя цыплятами, придуманное Роджером Пенроузом.














 Пермский край: инвестиционные возможности
Пермский край: инвестиционные возможности Системные платы Gigabyte
Системные платы Gigabyte Кроссворд на английском языке
Кроссворд на английском языке Проектирование системы электроснабжения электроаппаратного завода
Проектирование системы электроснабжения электроаппаратного завода Древние образы народного искусства
Древние образы народного искусства Решение квадратных уравнений
Решение квадратных уравнений Антимонопольное регулирование в авторитейле
Антимонопольное регулирование в авторитейле Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко
Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко Highlights of sports
Highlights of sports Просвещенный абсолютизм в России
Просвещенный абсолютизм в России Феофан Грек, Андрей Рублев
Феофан Грек, Андрей Рублев "Платон" - Философия
"Платон" - Философия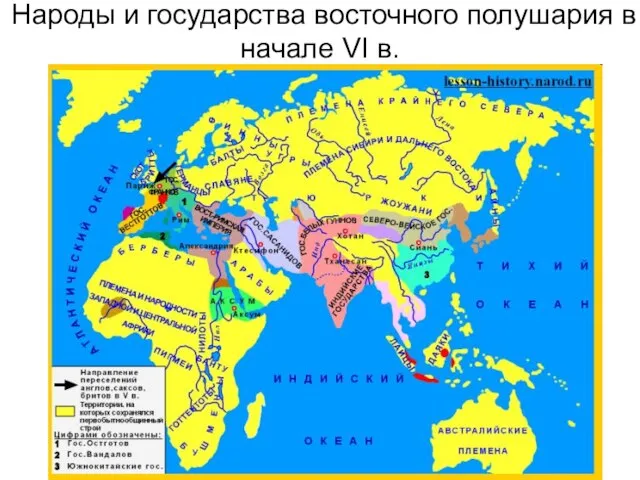 Народы и государства восточного полушария в начале VI в.
Народы и государства восточного полушария в начале VI в. Деятельность
Деятельность ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл
ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В.
ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В. Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле
Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле Реклама и маркетинг
Реклама и маркетинг Изображение цветка пиона в разных техниках художественной обработки
Изображение цветка пиона в разных техниках художественной обработки Мутационная изменчивость 10 класс
Мутационная изменчивость 10 класс Byredo Blanche. Парфюмерия
Byredo Blanche. Парфюмерия Элетромеханический замок с убегающим кодом
Элетромеханический замок с убегающим кодом Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Valentine game
Valentine game Аспартам
Аспартам Попечительский совет или Управляющий совет?
Попечительский совет или Управляющий совет? Компания Декорсталь – Производитель декоративных сталей
Компания Декорсталь – Производитель декоративных сталей Taller de comunicación oral y escrita
Taller de comunicación oral y escrita