ПИРАМИДА

Содержание
ОпределениеОпределение Определение пирамиды
Площадь пирамиды
Правильная пирамида
Свойство пирамиды
Апофема Теорема о площади боковой поверхности правильной пирамиды
Усеченная пирамида
Правильная усеченная пирамида
Теорема о площади боковой поверхности правильной усеченной пирамиды

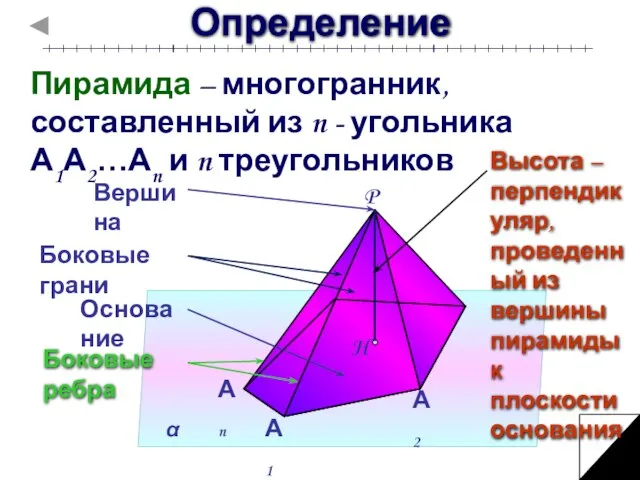
Определение
Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников
Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания
Боковые ребра

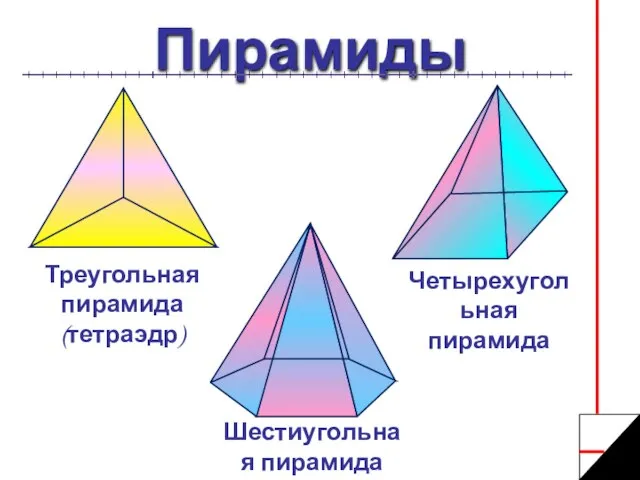
Пирамиды
Треугольная пирамида (тетраэдр)
Шестиугольная пирамида
Четырехугольная пирамида

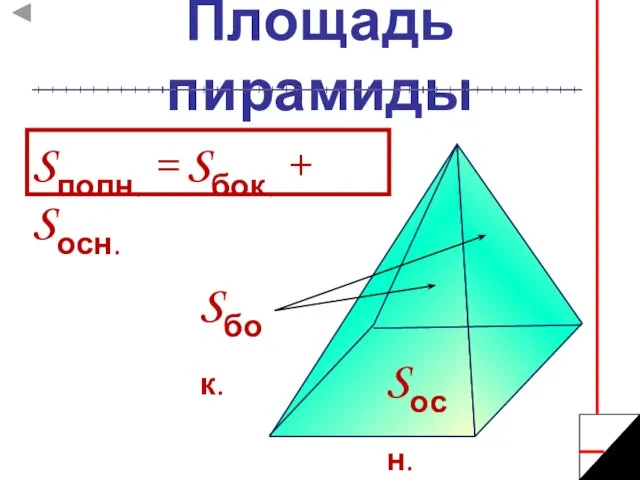
Площадь пирамиды
Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

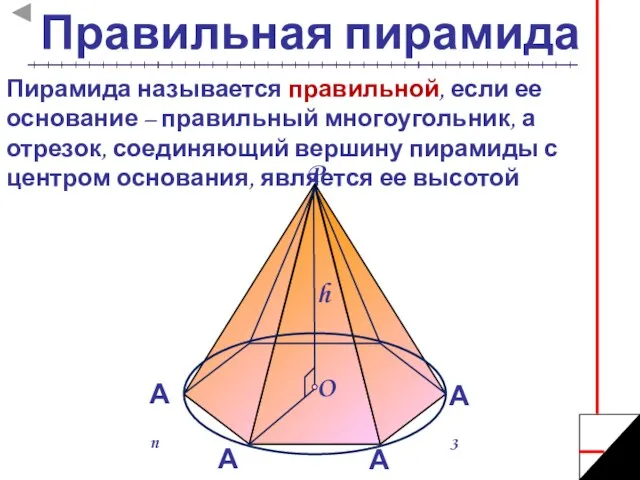
Правильная пирамида
Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой

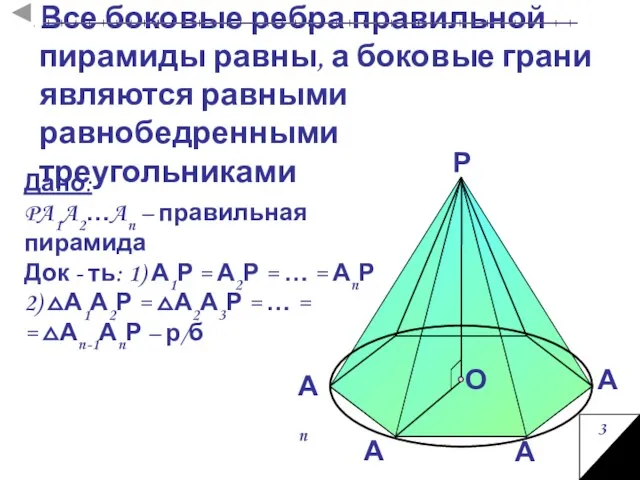
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками
Дано:
PA1A2…An – правильная пирамида
Док - ть: 1) А1Р = А2Р = … = АnР
2) △А1А2Р = △А2А3Р = … =
= △Аn-1АnР – р/б

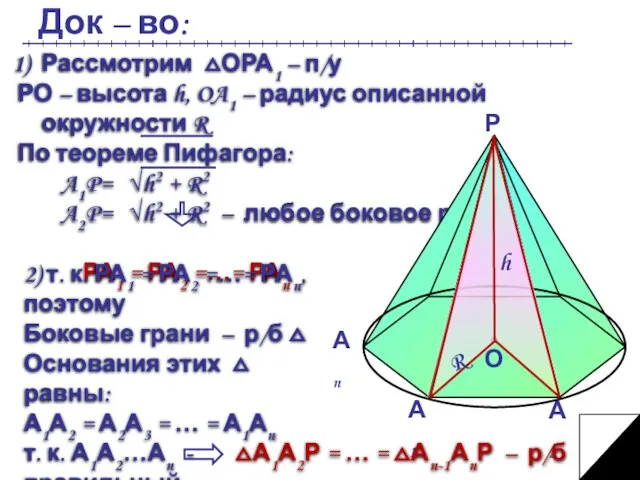
Док – во:
2) т. к. РА1 = РА2 =…= РАn, поэтому
Боковые грани – р/б △
Основания этих △ равны:
А1А2 = А2А3 = … = А1Аn
т. к. А1А2…Аn - правильный многоугольник
△А1А2Р = … = △Аn-1АnР – р/б

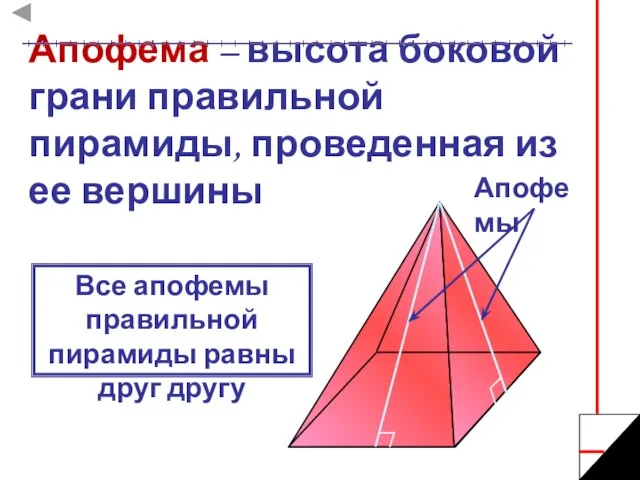
Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины
Апофемы
Все апофемы правильной пирамиды равны друг другу

Теорема о площади боковой
поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
Док – во:
Sбок = (½ad + ½ad + ½ad) =
= ½d(a + a + a)= ½dP
Sбок = ½dP

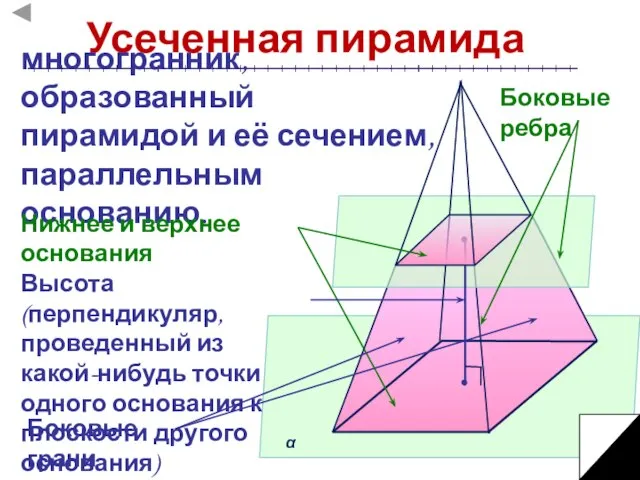
Усеченная пирамида
многогранник, образованный пирамидой и её сечением, параллельным основанию.
Нижнее и верхнее основания
Боковые грани
Боковые ребра
Высота (перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания)

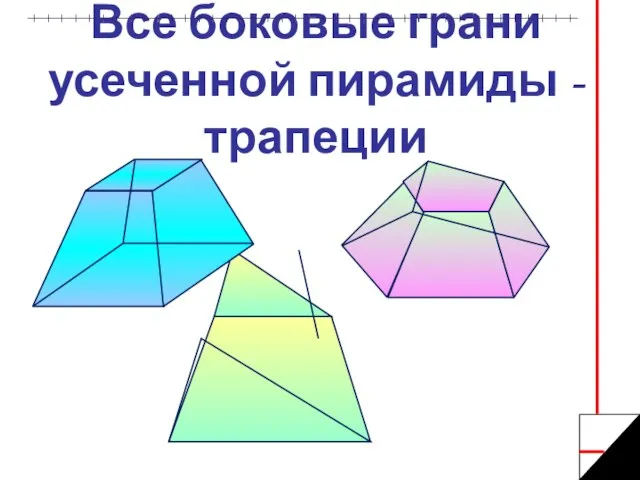
Все боковые грани усеченной пирамиды - трапеции

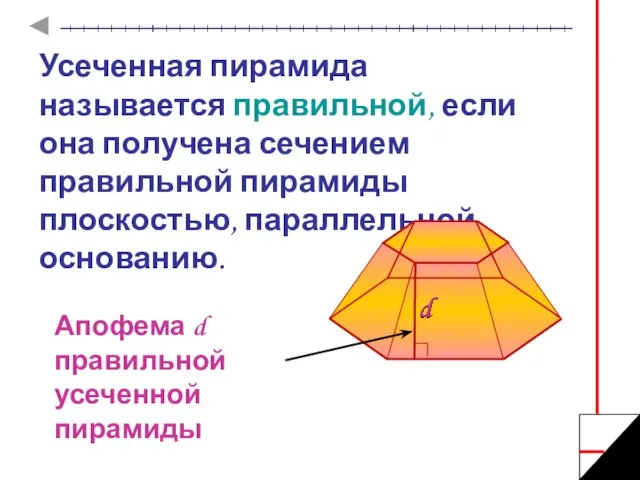
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.
Апофема d правильной усеченной пирамиды

Теорема о площади боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему
S бок = ½(Р1 + Р2) d
P1= 4a1
P2= 4a2
Док – во:
S бок = ½d(a1+a2) + ½d(a1+a2) +
+ ½ d(a1+a2) + ½d(a1+a2) =
= ½d(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) =
= ½d(4a1+ 4a2) = ½d(P1+ P2)