Слайд 2Пирамида – многогранник, состав –
ленный из угольника и треугольни –
ков, при этом

угольник считают ос –
нованием пирамиды, а треугольники – боковыми гранями.
Вершина пирамиды – общая вер –
шина всех боковых граней.
Боковые ребра – стороны боковых
граней, не лежащие в основании
пирамиды.
Слайд 3Например, OPSR - пирамида,O - вер-
шина пирамиды, OP, OS, OR ее боковые
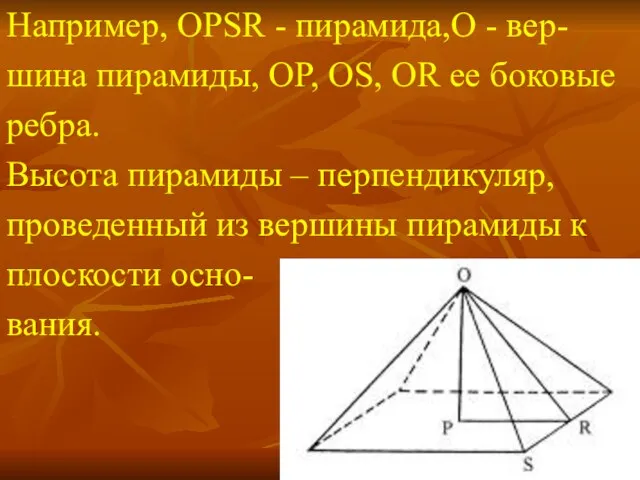
ребра.
Высота пирамиды – перпендикуляр,
проведенный из вершины пирамиды к
плоскости осно-
вания.
Слайд 4Площадь полной поверхности пира -
миды – это сумма всех ее граней.
Площадь боковой

поверхности пира-
миды – это сумма площадей ее боко-
вых граней.
Тетраэдр – треугольная пирамида,
все четыре грани которой – треу –
гольники, и любая из них может быть
принята за основание.
Слайд 5Правильные пирамиды
Правильная пирамида – пирами-
да, основание которой – правиль–
ный многоугольник, а отрезок

соединяющий вершину пирамиды с центром основания, является ее высотой.
Слайд 6Свойства правильной пирамиды:
1) Боковые рёбра правильной пирамиды
равны.
2)Боковые грани правильной пирамиды
являются

равными равнобедренными треу-
гольниками.
Слайд 7Апофема
Апофема – высота боковой грани
правильной пирамиды, проведен-
ная из вершин пирамиды.
Теорема о

площади боковой по-
верхности правильной пирами-
ды: площадь боковой поверхности
правильной пирамиды равна поло-
вине произведения периметра осно-
вания на апофему.
Слайд 8Усеченная пирамида
Усеченная пирамида – это много –
гранник, полученный в результате
пересечения пирамиды

плоскостью,
параллельной плоскости основания,
точнее та часть пирамиды, которая
находится между плоскостями сече –
ния и основания пирамиды.
Слайд 9Нижнее и верхнее основания усеченной
пирамиды – это грани, лежащие в пара –
лельных

плоскостях. Основания усе-
ченной пирамиды являются подоб –
ными многоугольниками.
Боковые грани усеченной пирамиды
четырехугольники, которые соеди -
няют верхнее и нижнее основания. Боковые грани усеченной пирами-
ды - трапеции.
Слайд 10
Высота усеченной пирамиды это перпендикуляр, проведенный из произвольной точки одного

основания к плоскости другого основания.
Правильная усеченная пира-
мида- усеченная пирамида, ос-
нования которой являются пра-
вильными многоугольниками, а
боковые грани- равнобедренными
трапеицями. Высоты боковых гра-
ней правильной усеченной пирами-
ды называют апофемами.









 Решение уравнений
Решение уравнений Грузовое устройство
Грузовое устройство Катаргина Наталья Юрьевна.
Катаргина Наталья Юрьевна. Новогоднее представление Мышеловка для Деда Мороза
Новогоднее представление Мышеловка для Деда Мороза Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация
Экосистема Digital-маркетинга в России: Основы навигациии X Саммит Брендов-Лидеров 7 июня 2011. - презентация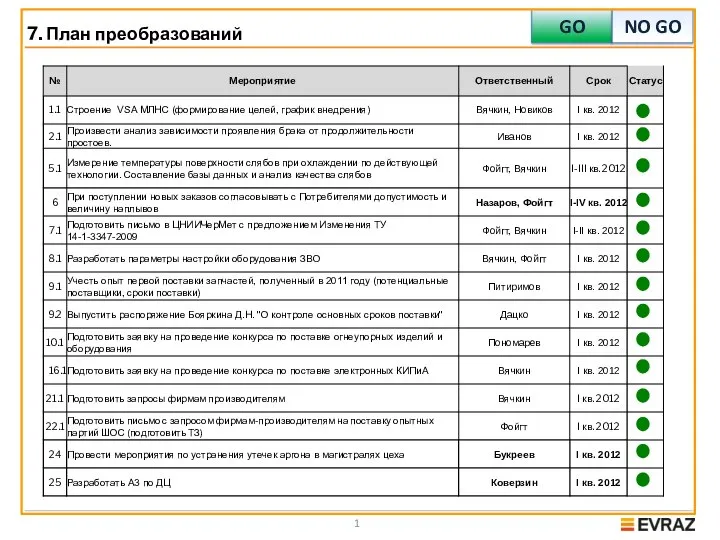 План преобразований. Отслеживание результатов
План преобразований. Отслеживание результатов Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка
Порядок получения статуса субъекта оптового рынка и права на участие в торговой системе оптового рынка  Поводы и основания к возбуждению уголовного дела
Поводы и основания к возбуждению уголовного дела Вольфганг Амадей Моцарт
Вольфганг Амадей Моцарт Съемки подземных сооружений и коммуникаций
Съемки подземных сооружений и коммуникаций Проблема истинной человечности в рассказе К. Паустовского “Телеграмма”
Проблема истинной человечности в рассказе К. Паустовского “Телеграмма” Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных
Вакцинация детей с перинатальным контактом по ВИЧ и ВИЧ-инфицированных Оценка рисков при проведении форвардных сделок
Оценка рисков при проведении форвардных сделок Управления их классификация
Управления их классификация Стратегия бизнес - проекта «Магазин без очередей и касс»
Стратегия бизнес - проекта «Магазин без очередей и касс» Город и транспорт
Город и транспорт Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное
Проектная грамотность. Как правильно подготовить заявку на финансирование проекта и реализовать задуманное Презентация на тему Ирак
Презентация на тему Ирак Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году
Объекты газоснабжения и водоснабжения, планируемые к реализации в 2020 году Ремонт электролизёров на месте установки
Ремонт электролизёров на месте установки Презентация на тему Японское море
Презентация на тему Японское море Ранний железный век в Казахстане
Ранний железный век в Казахстане Passato Reg
Passato Reg Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , «
Легендарное восклицание «Эврика!», принадлежит Архимеду , «Я нашел!» Легендарное восклицание «Эврика!», принадлежит Архимеду , « Этические и правовые нормы информационной деятельности человека
Этические и правовые нормы информационной деятельности человека Лекция 5 Модель классов предметной области (1)
Лекция 5 Модель классов предметной области (1) Осторожно - мошенники
Осторожно - мошенники Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму
Модернизация государственной семейной политики в современной России: (экстра)ординарный поворот к пронатализму