Пирамиды вокруг нас

Пирамиды вокруг нас
«А в немой дали застыли пирамиды
фараонов, саркофаги древней были.
Величавые как вечность, молчаливые как
смерть.»
Михай Эминеску

Рабочие группы
Математики
Историки
Исследователи мировой системы пирамид
Исследователи свойств пирамид
Архитекторы

Математическая точка зрения
Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости сходятся к одной точке.
Герон предложил следующее определение пирамиды: «Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник».

Математическая точка зрения
Адриен Мари Лежандр в своём труде «Элементы геометрии» в 1794 г. даёт определение: «Пирамида – телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания».
В учебнике XIX в. Фигурировало определение: «пирамида – телесный угол, пересечённый плоскостью».

Разворот учебника элементарной геометрии А. Киселева, 1907 г.

Историческая точка зрения
ПИРАМИДА, монументальное сооружение, имеющее геометрическую форму пирамиды (иногда ступенчатую или башнеобразную). Пирамидами называют гробницы древне-египетских фараонов
3 – 2-го тыс. до н. э., а также постаменты храмов в Центральной и Южной Америке, связанные с космологическими культами.
Терра-Лексикон: Иллюстрированный
энциклопердический словарь, 1998

Историческая точка зрения
Мексиканская пирамида Солнца
Ступенчатая пирамида в Египте

Исследование
мировой системы пирамид
Гора Кайлас на Тибете

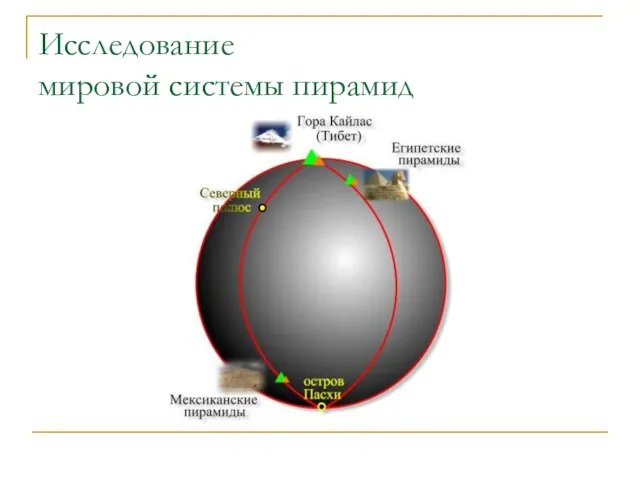
Исследование
мировой системы пирамид

Золотое сечение
ЗОЛОТОЕ СЕЧЕНИЕ, деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ. Приближённо это отношение равно 5/3, точнее 8/5, 13/8 и т. д. Принципы З. с. используются в архитектуре и в изобр. иск-вах. Термин «З. с.» ввёл Лернардо да Винчи (кон. 15 в.).

Исследование свойств пирамид
При постройке египетских пирамид было установлено, что квадрат, построенный на высоте пирамиды, в точности равен площади каждого из боковых треугольников. Это подтверждается новейшими измерениями.
Если сторону основания пирамиды разделить на точную длину года – 365,2422 суток, то получается 10-миллионная доля земной полуоси с большой точностью.

Исследование свойств пирамид
Мы знаем, что отношение между длиной окружности и её диаметром есть постоянная величина, хорошо известная современным математикам, школьникам – это число π = 3,1416… Но если сложить четыре стороны основания пирамиды Хеопса, мы получим 931,22 м. Разделив это число на удвоенную высоту пирамиды (2*148,208), мы получим 3,1416…, то есть число π.

Пирамиды в архитектуре
Стеклянная пирамида – новый вход в Лувр, Париж
Торговый центр в Илинге, Лондон

Группа «Математики»
Изучить пирамиду как геометрическое тело.
Найти определения пирамиды, которые были сформулированы древними учёными.
Сравнить современные трактовки с древними.

Группа «Историки»
Найти материалы о первых пирамидах.
Изучить древние пирамиды с математической точки зрения.
Сформулировать вывод о значимости пирамид с исторической и математической точек зрения.

Группа «Исследователи мировой системы пирамид»
Установить наличие мест расположения пирамид на Земле.
Установить связи между местами расположения пирамид.
Сформулировать вывод о расположении пирамид на Земле.

Группа «Исследователи свойств пирамид»
Исследовать уникальные свойства пирамид.
Подготовить материал о практическом применении свойств пирамид.