Плоское движение твердого тела

2
Лоуренс Хаусмен,
1865-1959, Bromsgrove

2
Bromsgrove

3
На предыдущей лекции
Сформулирован способ задания движения ТТ
Введено понятие степеней свободы Определено поступательное движение ТТ
Определено вращательное движение ТТ
Изучено вращение ТТ вокруг неподвижной
оси
Изучены кинематические характеристики
вращательного движения ТТ
Изучены передаточные механизмы

Цель лекции
Изучить плоское движение ТТ
9.1. Задание плоского движения ТТ
9.2. Скорости точек при плоском движении ТТ
9.3. Мгновенный центр скоростей
9.4. Ускорение точек при плоском движении ТТ
9.5. Кинематический расчет плоского
механизма
9.6. Заключение
4
План лекции

9.1. Задание плоского движения твердого тела
5

9.1.1. Определение и мотивация
2.1. ОПРЕДЕЛЕНИЕ ССС
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
6
Двигатель внутреннего сгорания
Движение твердого тела называется плоским (плоскопарал-лельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости

9.1.1. Определение и мотивация
2.1. ОПРЕДЕЛЕНИЕ ССС
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
7
Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу
Движение твердого тела называется плоским (плоскопарал-лельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости

9.1.1. Определение и мотивация
2.1. ОПРЕДЕЛЕНИЕ ССС
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
8
Иллюстрация работы кривошипно-шатунного механизма. Передача движения колесу
Движение твердого тела называется плоским (плоскопарал-лельным), если все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости

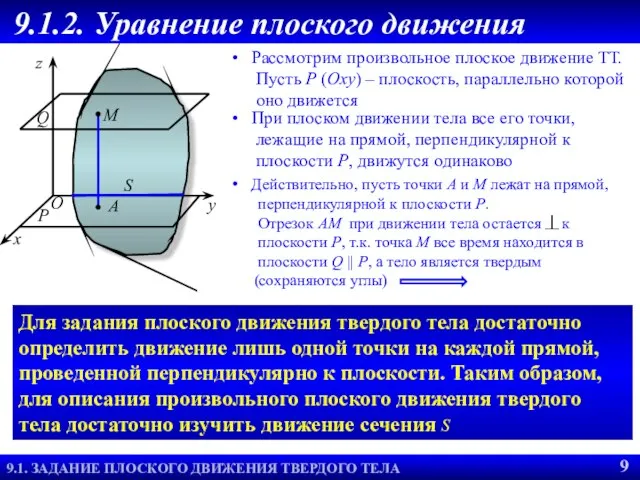
Рассмотрим произвольное плоское движение ТТ.
Пусть Р (Оху) – плоскость, параллельно которой
оно движется
Q
Р
9.1.2. Уравнение плоского движения
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
При плоском движении тела все его точки,
лежащие на прямой, перпендикулярной к
плоскости Р, движутся одинаково
Действительно, пусть точки А и М лежат на прямой,
перпендикулярной к плоскости Р.
Отрезок АМ при движении тела остается к
плоскости Р, т.к. точка М все время находится в
плоскости Q || Р, а тело является твердым
(сохраняются углы)
Т.о., отрезок АМ остается параллельным самому себе, т. е.
движется поступательно
А
М
Следовательно, точки А и М движутся с одинаковыми
скоростями
9
Для задания плоского движения твердого тела достаточно определить движение лишь одной точки на каждой прямой, проведенной перпендикулярно к плоскости. Таким образом, для описания произвольного плоского движения твердого тела достаточно изучить движение сечения S
S

Введем вспомогательную систему координат с
началом в точке А (полюсе) тела и осями ,
, параллельными соответствующим осям
неподвижной системы координат
Будем описывать движение сечения S
относительно неподвижной системы координат
Oxy, жестко связанной с плоскостью P
B
9.1.2. Уравнение плоского движения
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Положение сечения относительно этой системы
координат определяется положением какого-
либо принадлежащего ему отрезка AB
Этим степеням свободы соответствует движение
вдоль осей Оу и Ох и вращение относительно
некоторой точки
Т.о., из четырех координат, определяющих положение отрезка AB,
независимыми оказываются только три (3 степени свободы)
А
10
S
S
B
А
х1
у1
Система координат Ах1у1 будет двигаться
поступательно (со скоростью точки А)
относительно системы Оху
Положение отрезка АВ, а следовательно, и всего
сечения S относительно этой новой системы
координат, характеризуется углом φ. Движение
же отрезка АВ относительно системы координат
Ах1у1 – это вращательное движение
φ
Т.о., плоское движение ТТ слагается из поступательного
движения вместе с полюсом и вращения вокруг полюса
Это движение будет однозначно
определено, если заданы координаты
точки и угол между осью и отрезком
Т.о., закон плоского движения ТТ имеет вид

При задании этого закона движения за
полюс может быть взята любая точка тела
B
9.1.3. О выборе полюса
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поэтому вид первых двух уравнений зависит от выбора полюса, т. е.
поступательная часть движения зависит от выбора полюса.
Вращательная же часть движения от выбора полюса не зависит
Так как прямые АВ и СВ1 жестко связаны с телом и тело абсолютно
твердое, то эти прямые, будучи параллельными при t = 0, останутся
параллельными и при любом t > 0. Это и означает, что φC (t) = φА(t)
для любого t > 0.
Действительно,
А
11
С
B1
Пусть С – другой полюс, и пусть точка В1 такова, что в начальный
момент времени (при t = 0) φC (0) = φА(0).

Эти уравнения одновременно являются и
параметрическими уравнениями траектории точки М
Определим закон движения точек ТТ
9.1.4. Закон движения
9.1. ЗАДАНИЕ ПЛОСКОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Пусть точка М расположена на
расстоянии ρ = АМ от полюса А
12
М
А
α
φ

9.2. Скорости точек ТТ при плоском движении
13

Это скорость вращательного движения тела
в системе координат Ах1у1
Скорость произвольной точки М ТТ, совершающего плоское движение, геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости этой точки в ее вращении вместе с телом вокруг полюса
Скорость произвольной точки М находится
дифференцированием закона движения
9.2.1. Теорема о скоростях точек ТТ
9.2. СКОРОСТЬ ТОЧЕК ТВЕРДОГО ТЕЛА
где введена скорость движения точки М относительно полюса А
14
М
А
х1
у1
φ

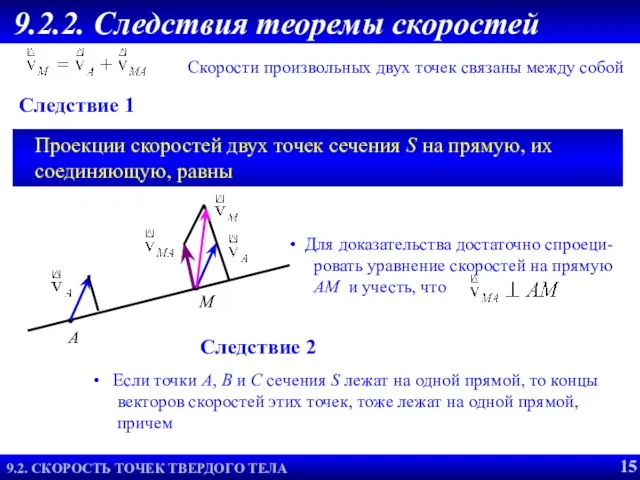
Проекции скоростей двух точек сечения S на прямую, их
соединяющую, равны
Следствие 1
9.2.2. Следствия теоремы скоростей
9.2. СКОРОСТЬ ТОЧЕК ТВЕРДОГО ТЕЛА
Для доказательства достаточно спроеци-
ровать уравнение скоростей на прямую
АМ и учесть, что
15
Скорости произвольных двух точек связаны между собой
М
А
Следствие 2
Если точки А, В и С сечения S лежат на одной прямой, то концы
векторов скоростей этих точек, тоже лежат на одной прямой,
причем

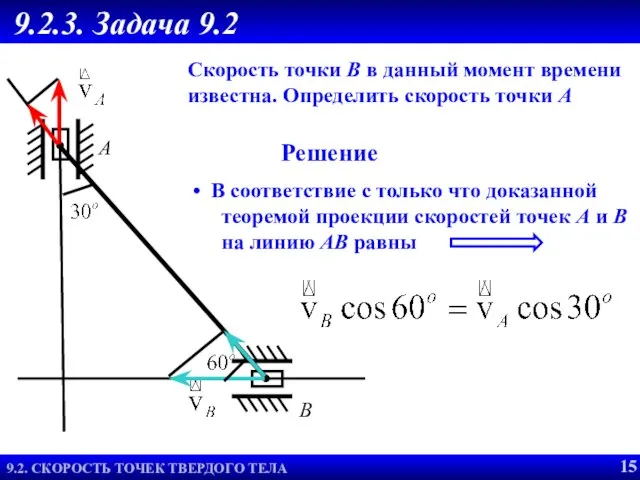
9.2.3. Задача 9.2
9.2. СКОРОСТЬ ТОЧЕК ТВЕРДОГО ТЕЛА
Решение
15
Скорость точки В в данный момент времени известна. Определить скорость точки А
В
А
В соответствие с только что доказанной
теоремой проекции скоростей точек А и В
на линию АВ равны

9.3. Мгновенный центр скоростей
16

Это следует из теоремы о проекциях скоростей, так
как если бы скорость была отлична от нуля, то
она одновременно должна была бы быть перпенди-
кулярна к АА’ и BB’. Последнее, однако,
невозможно в силу непараллельности скоростей
точек А и В
Мгновенным центром скоростей (МЦС) сечения тела (или плоской фигуры) называется точка, скорость которой в данный момент времени равна нулю
9.3.1. Теорема о МЦС
9.3. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
Если угловая скорость рассматриваемого сечения S в данный момент времени отлична от нуля, то мгновенный центр скоростей существует и единственен
Тогда точка C, лежащая на пересечении перпенди-
куляров соответственно к скоростям и , имеет
скорость, равную нулю, и, следовательно, является
МЦС
Теорема
17
C
Пусть в некоторый момент времени t точки A и B
имеют скорости, не параллельные друг другу
Действительно, рассмотрим сечение S
B
А
S
А’
B’
Теорема доказана

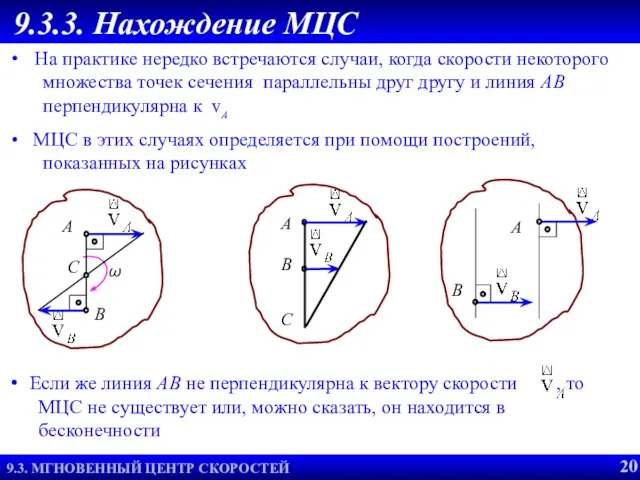
Но поскольку
Т.о., для определения МЦС надо знать только направления скоростей каких-
либо двух точек сечения тела (или касательные к траекториям этих точек)
9.3.2. Использование МЦС
9.3. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
МЦС находится в точке пересечения перпендикуляров, восстановленных из
этих точек к их скоростям
18
Аналогично для любой другой точки сечения
Если в момент времени t, когда точка C является МЦС, взять ее за полюс, то
скорость любой точки сечения будет равна ее скорости вращения вокруг
МЦС
Поэтому, зная положение МЦС данной плоской фигуры и
скорость какой-либо ее точки, можно определить скорость
любой другой точки фигуры и ее угловую скорость

При определении скоростей точек тела плоское движение можно
представить как последовательность мгновенных вращений
вокруг мгновенного центра скоростей, который сам
перемещается в плоскости движения тела
МЦС может быть найден, если известны скорость одной точки тела,
например A, и линия действия скорости второй точки тела, например, B
9.3.3. Нахождение МЦС
9.3. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
Восстановив перпендикуляры к вектору скорости точки
A и к линии действия скорости точки B, находим точку
их пересечения C, которая и будет МЦС
19
Вращение тела происходит туда, куда вектор скорости
vA первой точки поворачивает тело вокруг МЦС
ω
B
C
A

Если же линия АВ не перпендикулярна к вектору скорости , то
МЦС не существует или, можно сказать, он находится в
бесконечности
На практике нередко встречаются случаи, когда скорости некоторого
множества точек сечения параллельны друг другу и линия АВ
перпендикулярна к vA
9.3.3. Нахождение МЦС
9.3. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
20
МЦС в этих случаях определяется при помощи построений,
показанных на рисунках
ω
A
С
B
С
A
В

9.4. Ускорение точек ТТ при плоском движении
21

Теорема о сложении ускорений
Ускорение любой точки тела, совершающего плоское движение, определяется как сумма ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса
9.3. УСКОРЕНИЯ ТОЧЕК ТТ ПРИ ПЛОСКОМ ДВИЖЕНИИ
22
9.4.1. Теорема о сложении ускорений точек
Доказательство
Теорема доказана
A
B

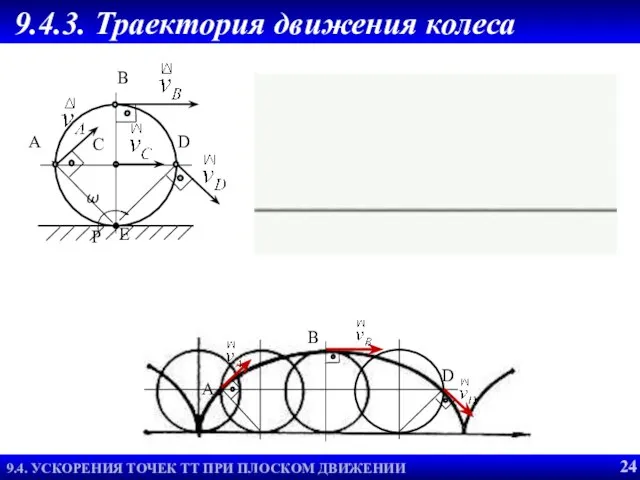
Согласно свойствам МЦС мы можем представить колесо, вращающимся в
данное мгновение времени вокруг МЦС
9.4.2. Задача 9.1
Решение
Колесо катится без скольжения по прямолинейному горизонтальному рельсу. Скорость его центра О равна vО. Найти скорости концов A, B, D, E вертикального и горизонтального диаметров колеса.
Решим задачу, используя свойства МЦС
Качение колеса происходит без скольже-
ния и МЦС колеса С будет находиться в
данный момент времени в точке касания
колеса с неподвижным рельсом, т.е.
vE = 0
МЦС

Вместо проверки

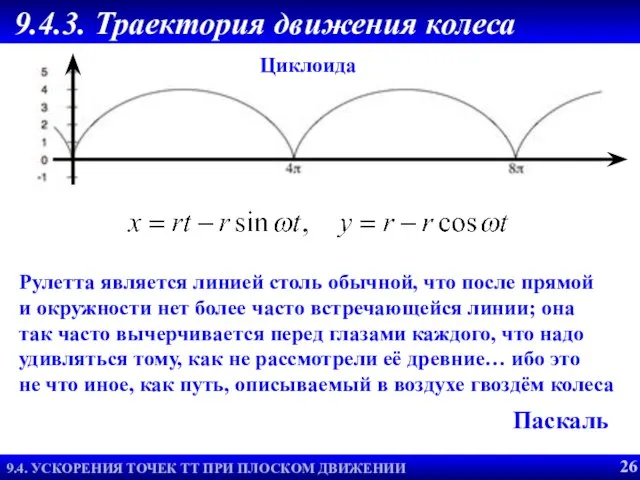
Циклоида
Рулетта является линией столь обычной, что после прямой
и окружности нет более часто встречающейся линии; она
так часто вычерчивается перед глазами каждого, что надо
удивляться тому, как не рассмотрели её древние… ибо это
не что иное, как путь, описываемый в воздухе гвоздём колеса
Паскаль

9.5. Расчет плоского механизма
27

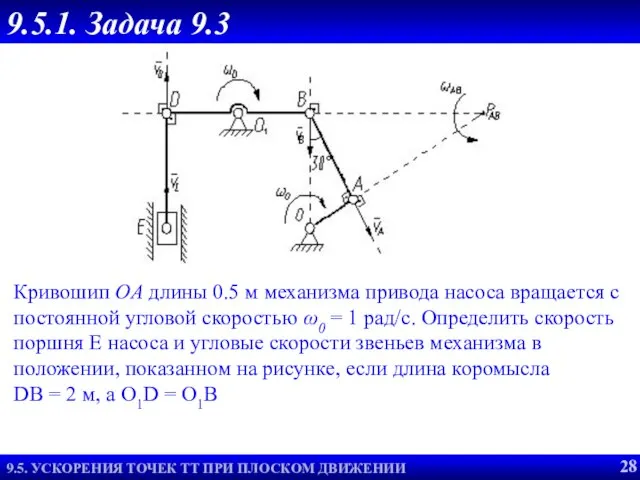
Пример 2.
Кривошип OA длины 0.5 м механизма привода насоса вращается с постоянной угловой скоростью ω0 = 1 рад/с. Определить скорость поршня E насоса и угловые скорости звеньев механизма в положении, показанном на рисунке, если длина коромысла
DB = 2 м, а O1D = O1B

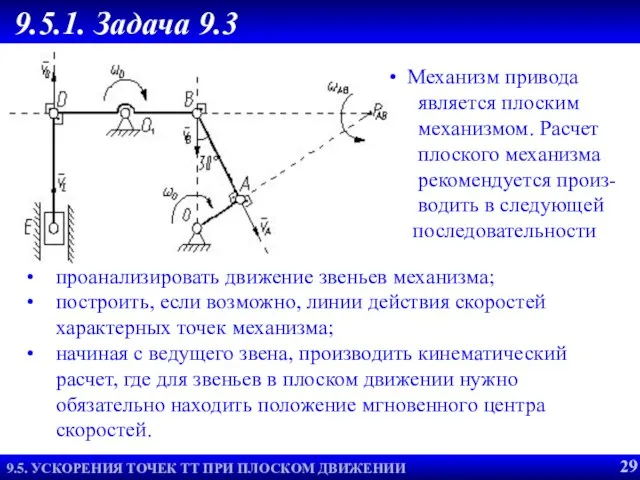
Пример 2.
Механизм привода
является плоским
механизмом. Расчет
плоского механизма
рекомендуется произ-
водить в следующей
последовательности
проанализировать движение звеньев механизма;
построить, если возможно, линии действия скоростей характерных точек механизма;
начиная с ведущего звена, производить кинематический расчет, где для звеньев в плоском движении нужно обязательно находить положение мгновенного центра скоростей.

9.6.1. Основные выводы
ЗАКЛЮЧЕНИЕ
Введено понятие плоского движения ТТ
Показано, что при плоском движении скорости
точек ТТ связаны между собой
Движение произвольной точки можно
представить в виде суперпозиции движения
некоторой другой точки (полюса) и вращения
относительно этого полюса
Плоское движение ТТ можно рассматривать
как вращение относительно МЦС