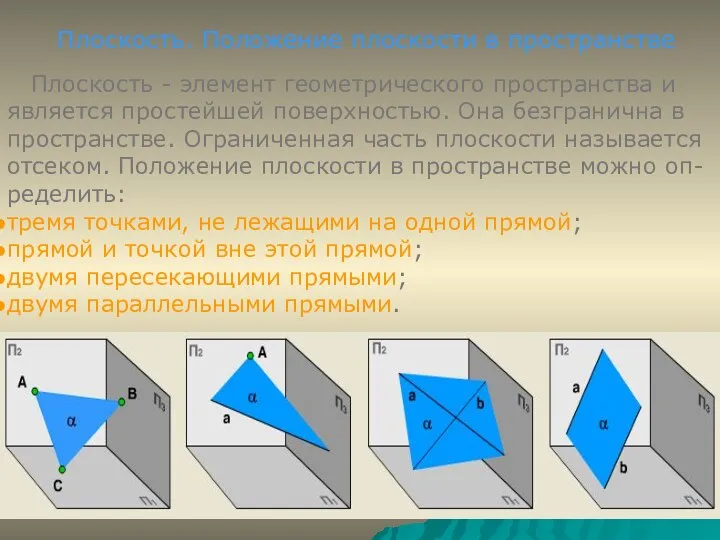
Плоскость. Задание и изображение плоскости на чертеже. Лекция 2

Плоскость. Положение плоскости в пространстве
Плоскость - элемент геометрического пространства и является простейшей поверхностью. Она безгранична в
пространстве. Ограниченная часть плоскости называется
отсеком. Положение плоскости в пространстве можно оп-
ределить:
тремя точками, не лежащими на одной прямой;
прямой и точкой вне этой прямой;
двумя пересекающими прямыми;
двумя параллельными прямыми.

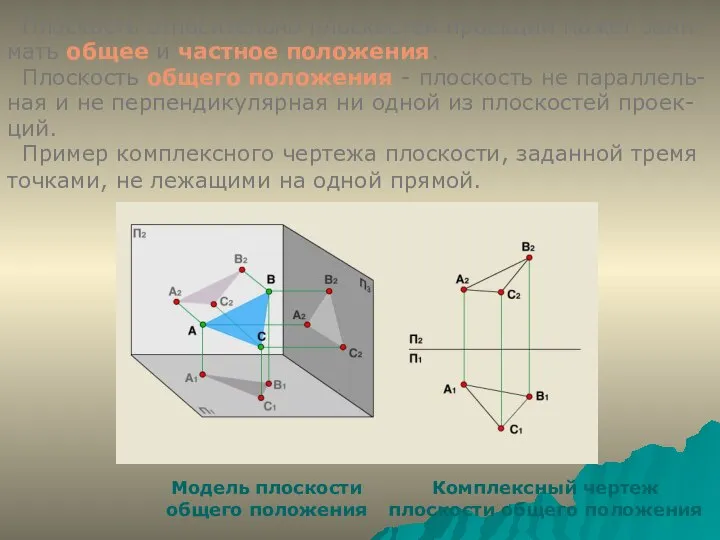
Плоскость относительно плоскостей проекций может зани-
мать общее и частное положения. Плоскость общего положения - плоскость не параллель-
ная и не перпендикулярная ни одной из плоскостей проек-
ций.
Пример комплексного чертежа плоскости, заданной тремя
точками, не лежащими на одной прямой.
Модель плоскости общего положения
Комплексный чертеж плоскости общего положения

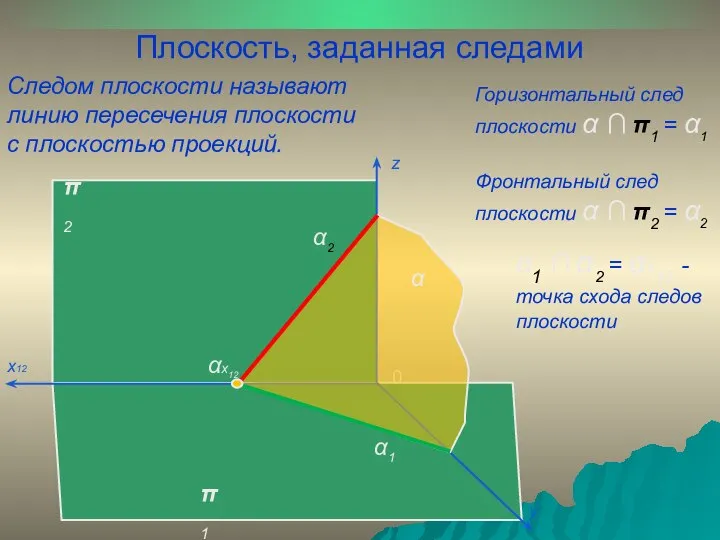
Плоскость, заданная следами
Следом плоскости называют
линию пересечения плоскости
с плоскостью проекций.
π 1
π 2
х12 0
z
y
α
Горизонтальный след
плоскости α ∩ π1 = α1
α1
αх12
Фронтальный след
плоскости α ∩ π2 = α2
α2
α1 ∩ α2 = αх12 - точка схода следов
плоскости

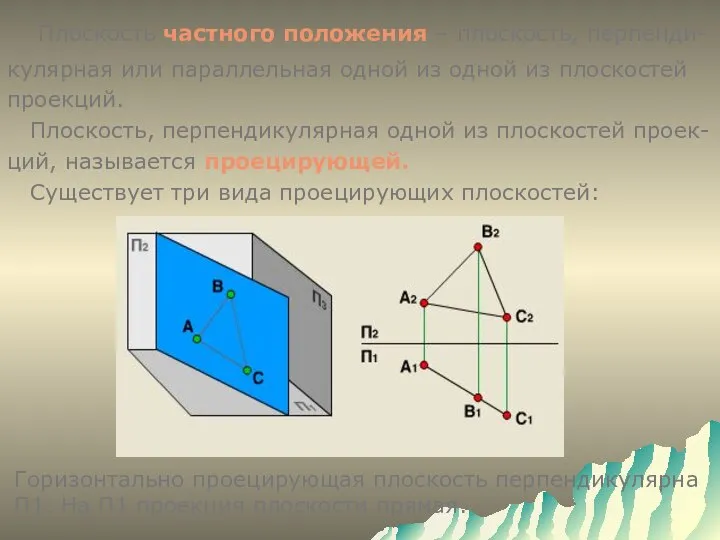
Плоскость частного положения – плоскость, перпенди-
кулярная или параллельная одной из одной из плоскостей
проекций.
Плоскость, перпендикулярная одной из плоскостей проек-
ций, называется проецирующей.
Существует три вида проецирующих плоскостей:
Горизонтально проецирующая плоскость перпендикулярна
П1. На П1 проекция плоскости прямая.

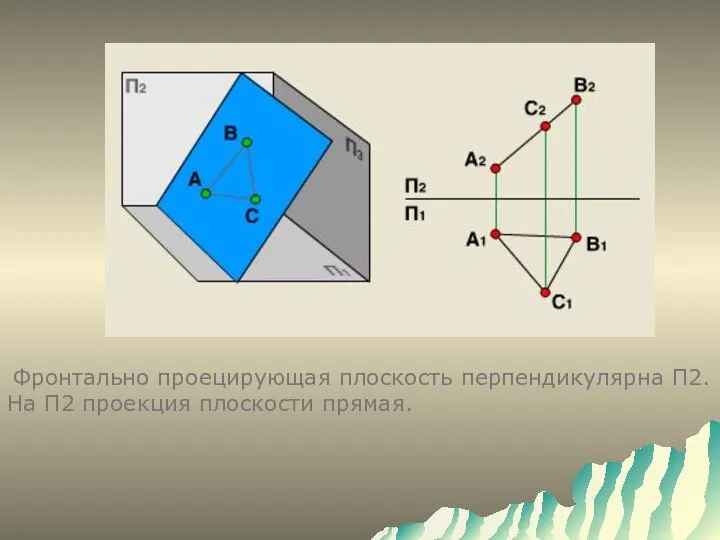
Фронтально проецирующая плоскость перпендикулярна П2. На П2 проекция плоскости прямая.

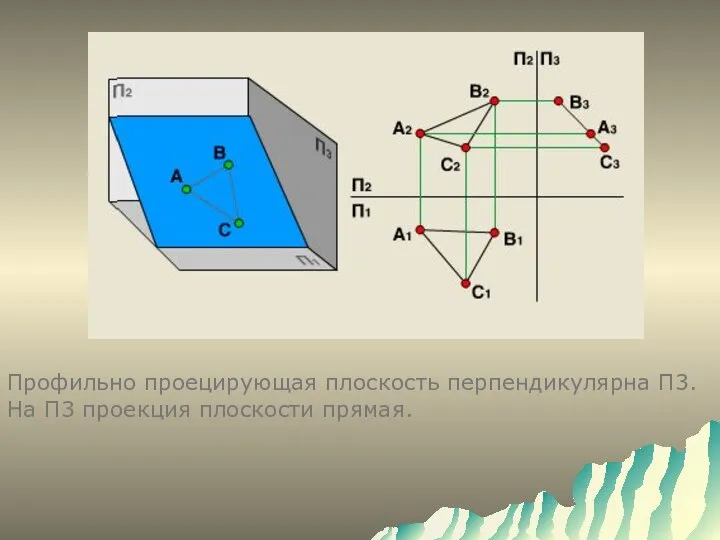
Профильно проецирующая плоскость перпендикулярна П3. На П3 проекция плоскости прямая.

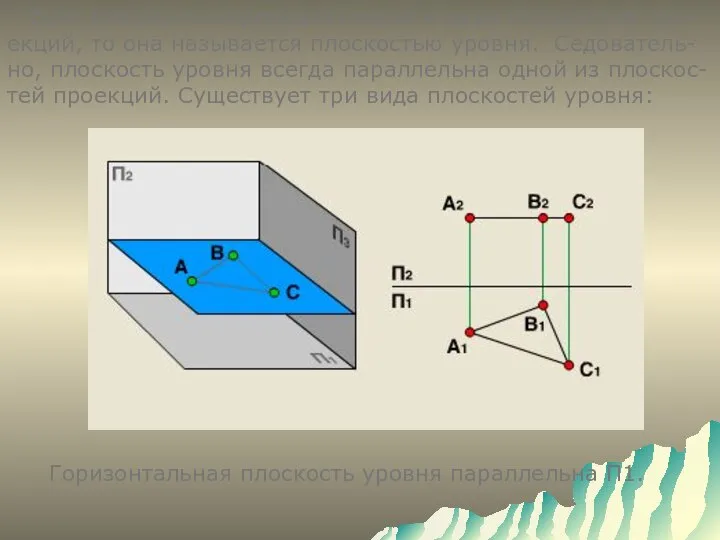
Если плоскость перпендикулярна к двум плоскостям про-
екций, то она называется плоскостью уровня. Седователь-но, плоскость уровня всегда параллельна одной из плоскос- тей проекций. Существует три вида плоскостей уровня:
Горизонтальная плоскость уровня параллельна П1.

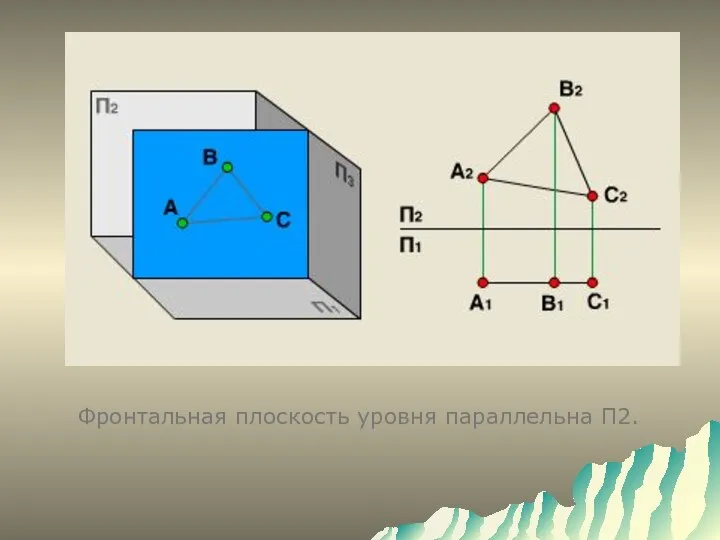
Фронтальная плоскость уровня параллельна П2.

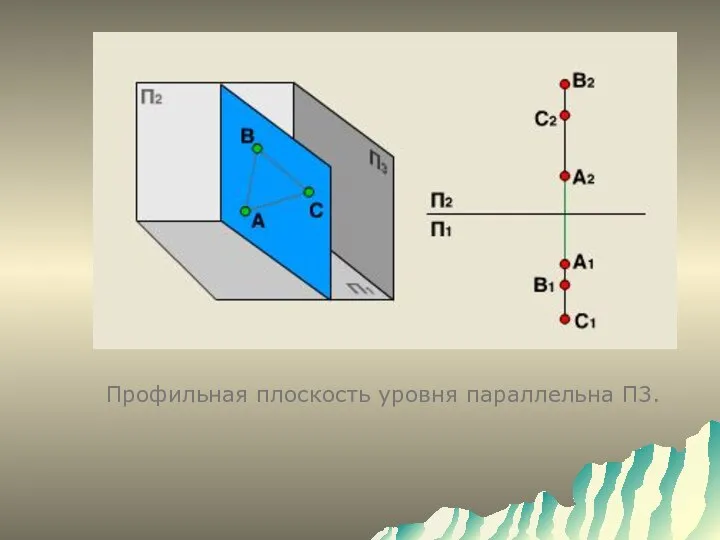
Профильная плоскость уровня параллельна П3.

Прямая и точка в плоскости
Построение прямой, находящейся в данной плоскости ос-
новано на двух известных положениях геометрии:
1. Прямая принадлежит плоскости, если она проходит че-
рез две точки, лежащие в данной плоскости, и обратно:
точка принадлежит плоскости, если она находится на пря-
мой, расположенной в плоскости.
2. Прямая принадлежит плоскости, если она проходит че-
рез точку, лежащую в данной плоскости, и параллельная
Какой-либо прямой, лежащей в плоскости.

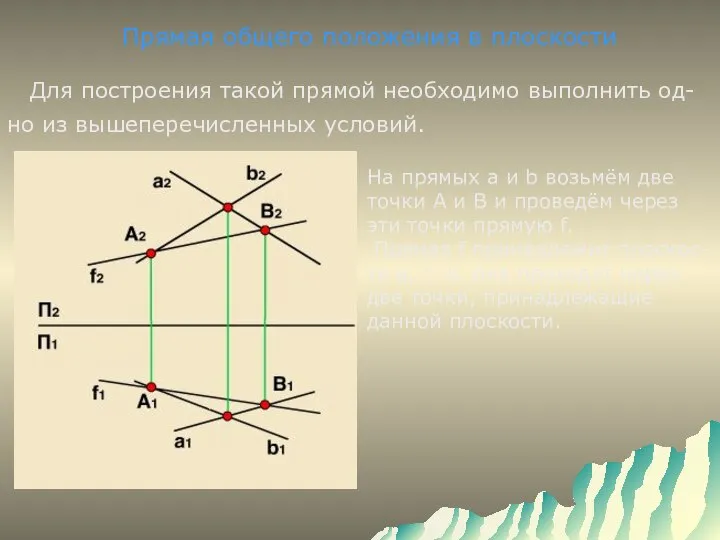
Прямая общего положения в плоскости
Для построения такой прямой необходимо выполнить од-
но из вышеперечисленных условий.
На прямых a и b возьмём две точки А и В и проведём через эти точки прямую f.
Прямая f принадлежит плоскос-ти a, т. к. она проходит через две точки, принадлежащие данной плоскости.

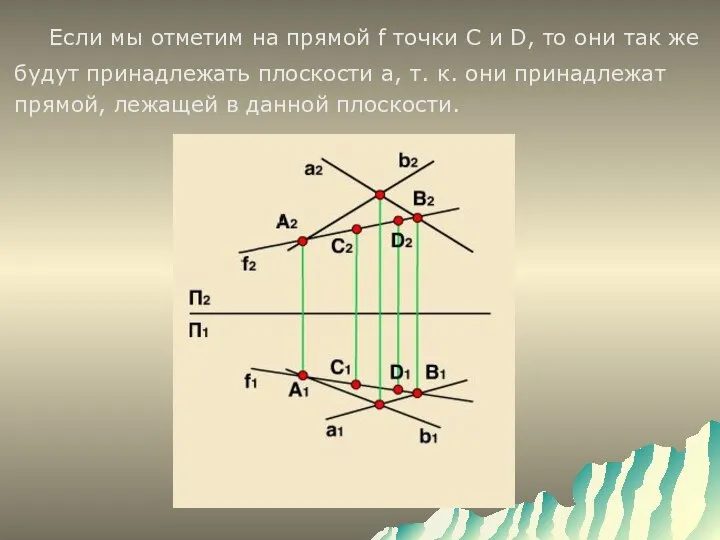
Если мы отметим на прямой f точки С и D, то они так же
будут принадлежать плоскости a, т. к. они принадлежат
прямой, лежащей в данной плоскости.

Особые линии плоскости
Прямые уровня - это прямые, принадлежащие плоскости и
параллельные какай - либо плоскости проекций. Эти пря-
мые называют прямыми уровня, так как они принадлежат
плоскости уровня. Существует три вида прямых уровня:
h - горизонталь плоскости - прямая принадлежащая
данной плоскости и || П1;
f - фронталь плоскости - прямая принадлежащая данной
плоскости и || П2;
w - профильная прямая плоскости – прямая принадле-
жащая данной плоскости и || П3.
Ниже приводится построение линии уровня на примере
горизонтали, принадлежащей плоскости α (∆ АВС).

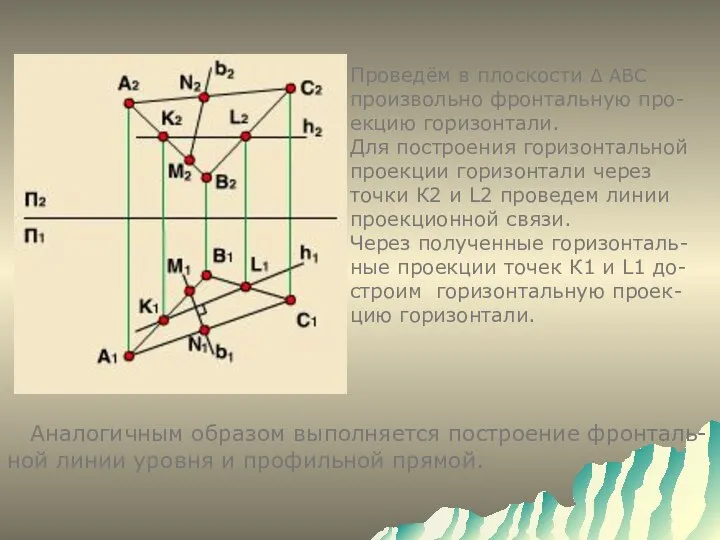
Проведём в плоскости ∆ АВС
произвольно фронтальную про- екцию горизонтали.
Для построения горизонтальной проекции горизонтали через точки К2 и L2 проведем линии проекционной связи.
Через полученные горизонталь-ные проекции точек К1 и L1 до-
строим горизонтальную проек-цию горизонтали.
Аналогичным образом выполняется построение фронталь-
ной линии уровня и профильной прямой.

Взаимное положение двух плоскостей
Плоскости могут быть параллельными, перпендикулярны-
ми друг другу, пересекаться.
Параллельные плоскости
Еcли две пересекающиеся прямые одной плоскости парал-
лельны двум пересекающимся прямым другой плоскости, то
такие плоскости параллельны.
Пусть дана плоскость α, заданная ∆ АВС и произвольная
точка D. Требуется через точку D провести плоскость b
параллельную α (∆ АВС). Для того чтобы через точку D
провести плоскость параллельную плоскости α (∆ АВС),
достаточно построить две пересекающиеся прямые, парал-
лельные двум пересекающимся прямым плоскости α, так
чтобы точка D принадлежала этим прямым.

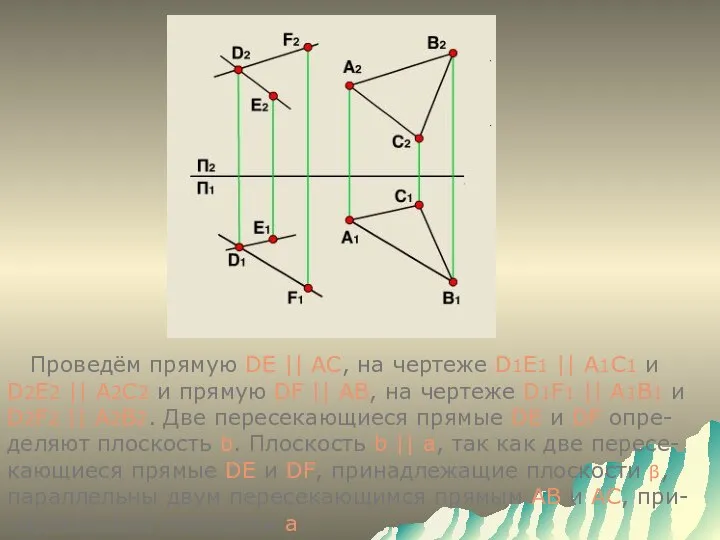
Проведём прямую DE || AC, на чертеже D1E1 || А1С1 и D2E2 || А2С2 и прямую DF || AB, на чертеже D1F1 || А1B1 и D2F2 || А2B2. Две пересекающиеся прямые DE и DF опре-
деляют плоскость b. Плоскость b || a, так как две пересе- кающиеся прямые DE и DF, принадлежащие плоскости β, параллельны двум пересекающимся прямым АВ и АС, при- надлежащим плоскости a.

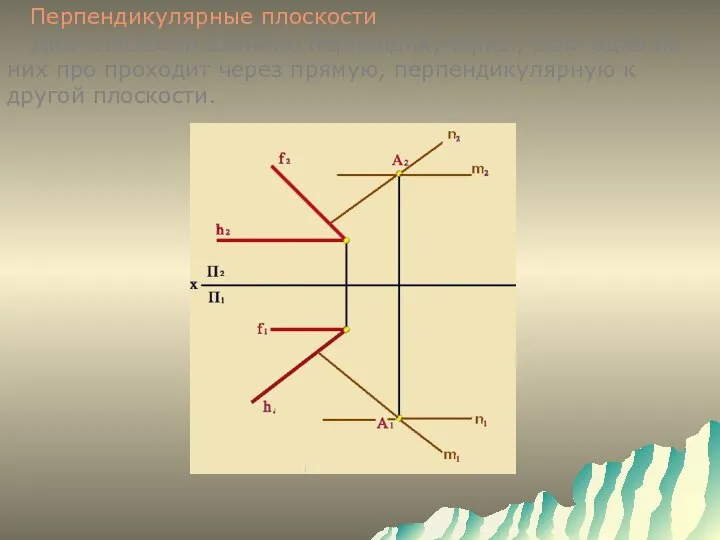
Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них про проходит через прямую, перпендикулярную к другой плоскости.

Чтобы через точку А провести плоскость, перпендикуляр- ную плоскости α(h α(h, f),, f), необходимо из точки А провести прямую n, перпендикулярную плоскости α(h, f) (горизонтальная проекция n1 перпендикулярна горизон- тальной проекции горизонтали h1, фронтальная проекция n2 перпендикуляр рна фронтальной проекции фронтали f2). Любая плоскость, проходящая через прямую n, будет пер-пендикулярна плоскости α(h,f), поэтому для задания плос- кости через точку А проводим произвольную прямую m.
Плоскость заданная двумя пересекающимися прямыми m и n, будет перпендикулярна плоскости α(h, f).

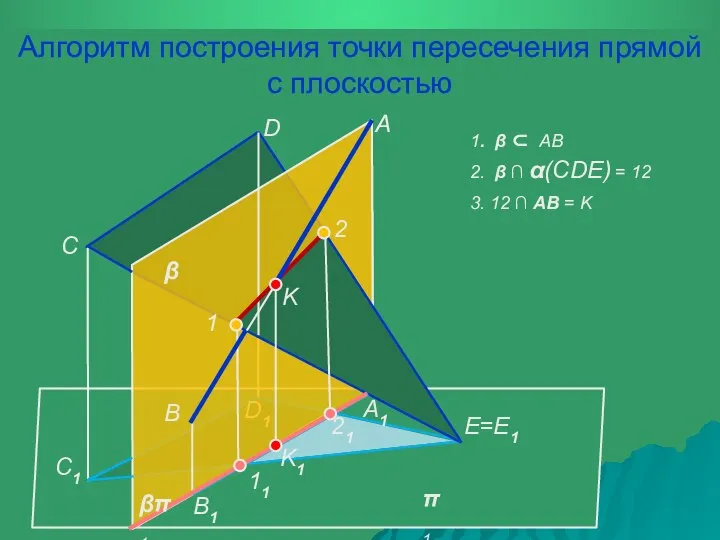
π 1
A
D1
B1
B
A1
β
βπ 1
C1
C
D
E=E1
11
21
1
K
K1
2
1. β ⊂ AB
2. β ∩ α(CDE) = 12
3. 12 ∩ AB = K
Алгоритм построения точки пересечения прямой с плоскостью