Содержание
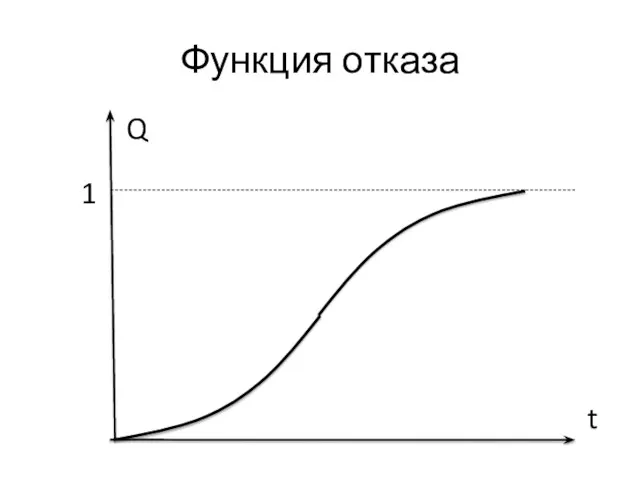
- 2. Функция отказа Q t 1
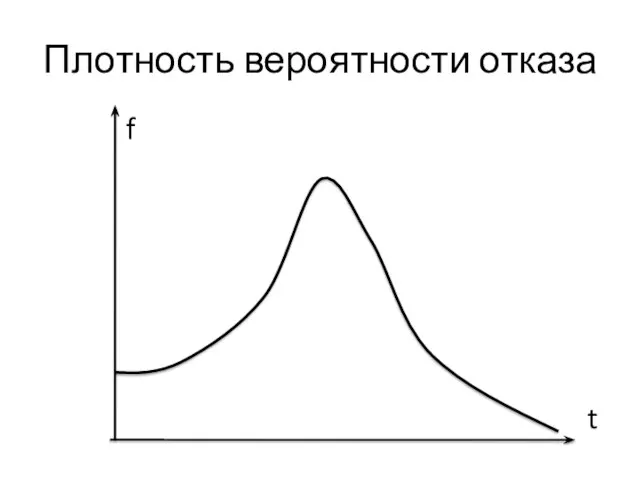
- 3. Введем понятие плотности вероятности отказа объекта f(t). Аналитически: f(t) = Q’(t). Статистически: где m(t) – количество
- 4. Плотность вероятности отказа f t
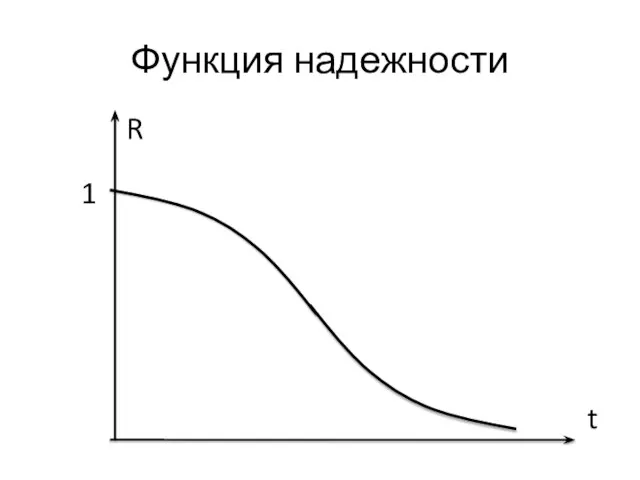
- 5. Обозначим вероятность безотказной работы в течение времени t: R(t) = P(T > t) Назовём R(t) функцией
- 6. Функция надежности R t 1
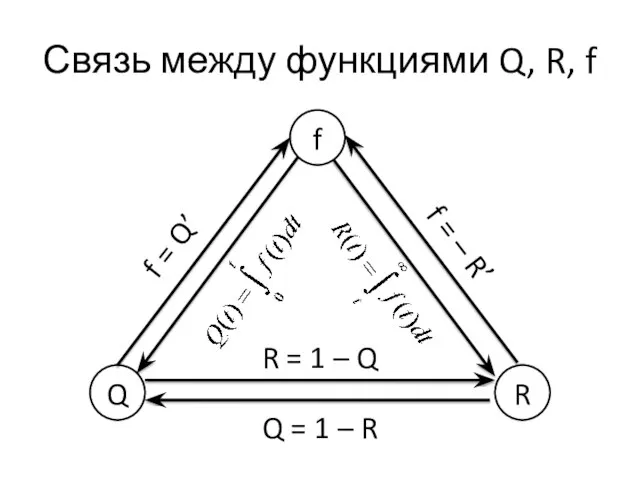
- 7. Связь между функциями Q, R, f Q R f Q = 1 – R R =
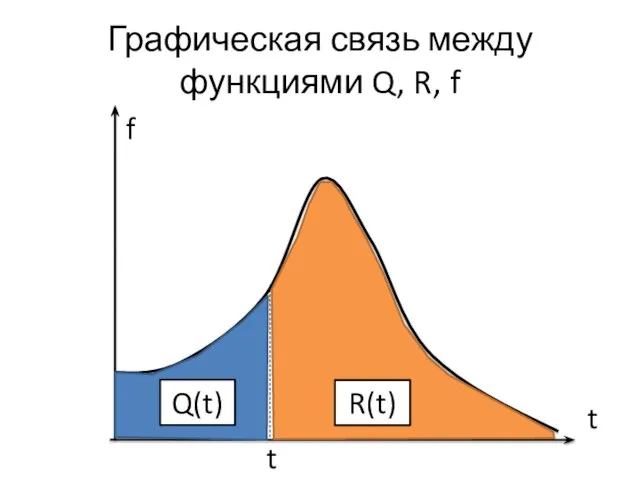
- 8. Графическая связь между функциями Q, R, f f t t Q(t) R(t)
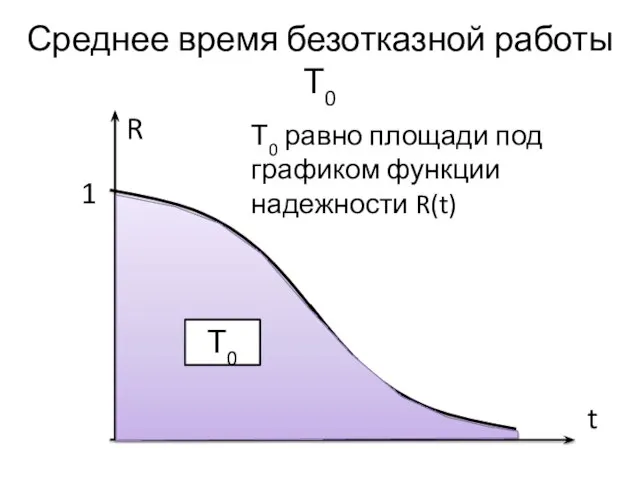
- 9. Среднее время безотказной работы Т0 R t 1 Т0 Т0 равно площади под графиком функции надежности
- 10. Среднее время безотказной работы Т0 Статистически: где ti – наработка до отказа i-го объекта; N0 –
- 11. Среднее время безотказной работы Т0 Если нет возможности дожидаться отказа всех объектов (из-за недостатка времени), то
- 12. Интенсивность отказов λ(t) [λ] = с-1, ч-1, год-1 и т. д. Статистически: λ(t) – число отказов
- 13. Интенсивность отказов λ(t) Аналитически: Статистически: где m(Δt) – количество отказов за время Δt.
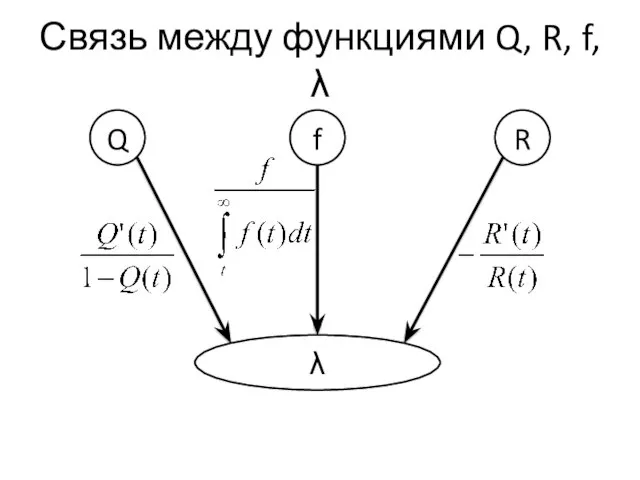
- 14. Связь между функциями Q, R, f, λ Q R f λ
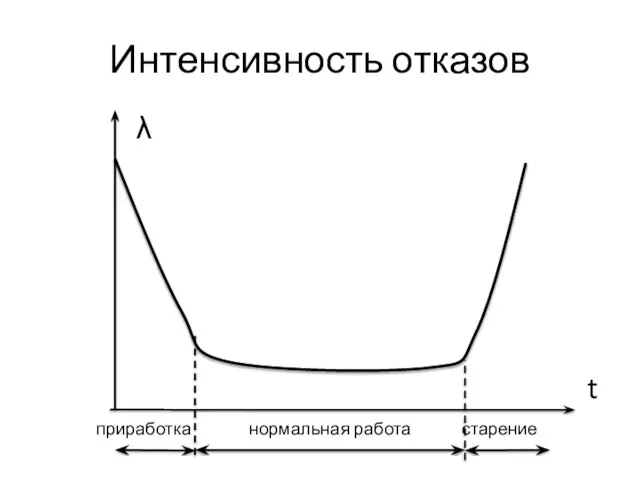
- 15. Интенсивность отказов λ t приработка нормальная работа старение
- 16. Для нормальной работы можно считать: λ(t) = const = λ Тогда R(t) = exp(– λt) Q(t)
- 17. При экспоненциальном законе вероятность безотказной работы на интервале (t; t + Δt) не зависит от времени
- 18. Упрощение формул для малых времён t В практических расчетах при малых временах рассмотренные выше формулы упрощают,
- 19. 3.2. Объекты с мгновенным восстановлением Эксплуатация восстанавливаемого объекта не прекращается при его отказе. Объект ремонтируется или
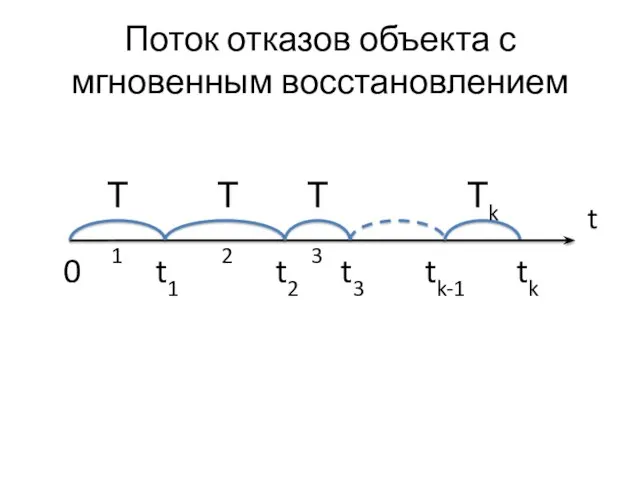
- 20. Поток отказов объекта с мгновенным восстановлением t Т1 Т2 Т3 Тk t1 t2 t3 tk tk-1
- 21. Рассмотрим плотности вероятностей времени: до первого отказа f1(t); до второго отказа f2(t); … до k-го отказа
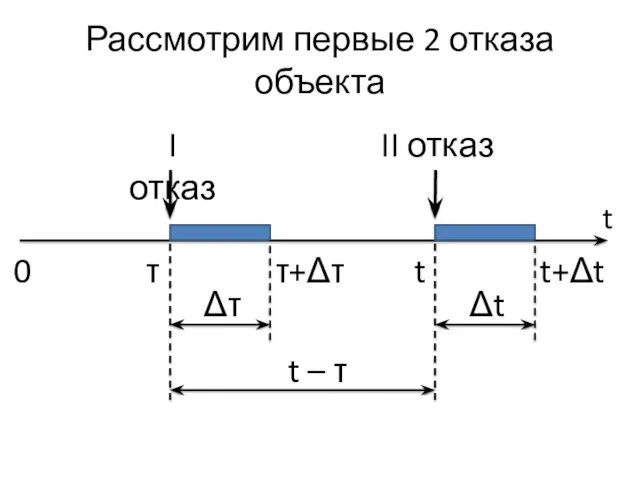
- 22. Рассмотрим первые 2 отказа объекта t I отказ τ τ+Δτ Δτ t+Δt t 0 II отказ
- 23. Выведем формулу для f2(t) Наработка на второй отказ равна t – τ. Рассмотрим вероятность того, что
- 24. Обобщим этот результат на k отказов. Выведем формулу для fk(t). Пояснение: Дошли до (k – 1)-го
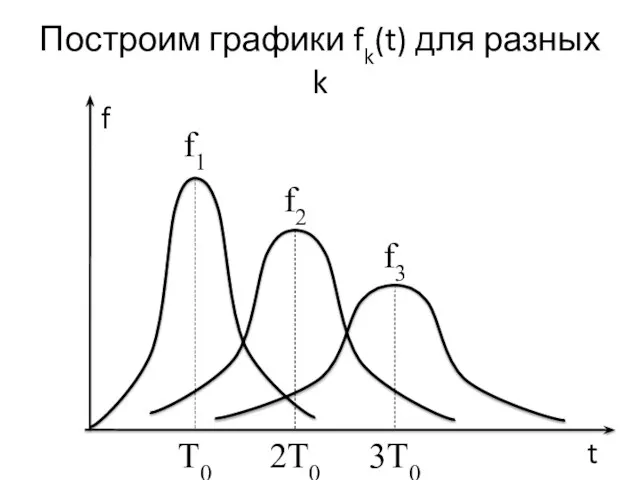
- 25. Построим графики fk(t) для разных k f t 2T0 T0 3T0 f1 f2 f3
- 26. Свойства графиков fk(t) Каждый график fk(t) имеет максимум в точке t = kТ0. Каждый график fk(t)
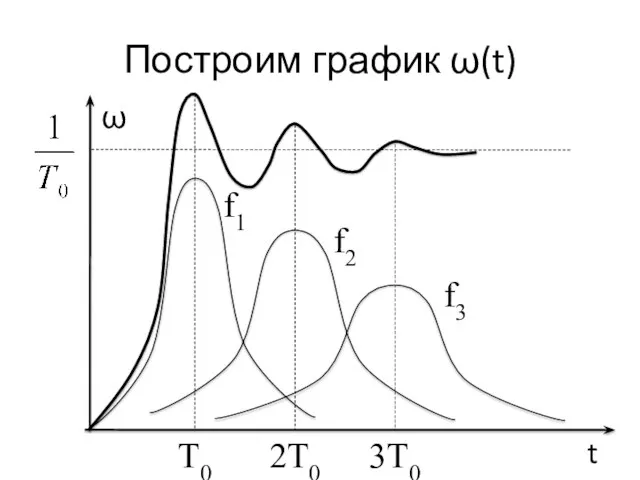
- 27. Параметр потока отказов ω(t) Назовём сумму f1(t) + f2(t) + … + fk(t) = ω(t) параметром
- 28. Построим график ω(t) ω t 2T0 T0 3T0 f1 f2 f3
- 29. Свойство графика ω(t) График ω(t) имеет максимумы в точках t = kТ0. Кривая ω(t) стабилизируется с
- 30. Свойства потоков отказов Потоки отказов могут обладать свойствами: Свойство ординарности. Вероятность совмещение 2-х и более отказов
- 31. Виды потоков отказов Если выполняется (1), то поток ординарный. Если выполняются (1) и (2), то поток
- 32. Для простейшего потока: f1(t) = λ exp(–λt) f2(t) = λ2 exp(–λt) … ω(t) = λ T0
- 33. Для простейшего потока: Вероятность k отказов за время t: Вероятность безотказной работы за время t: P0(t)
- 34. 3.3. Объекты с конечным временем восстановления Время восстановления τ = tп + tр tп – поиск
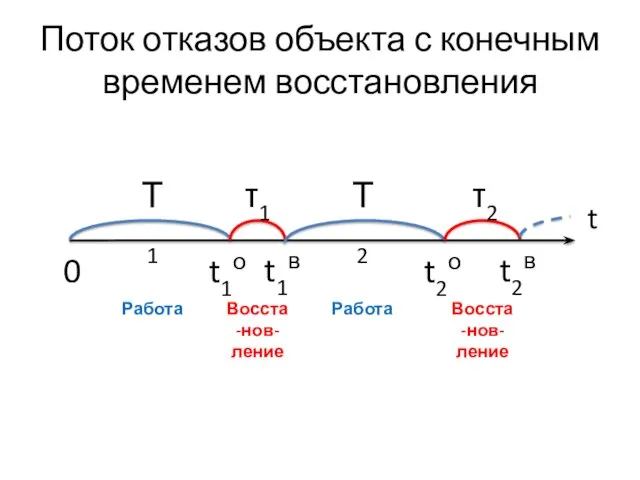
- 35. Поток отказов объекта с конечным временем восстановления t Т1 τ1 Т2 τ2 t1о 0 t1в t2о
- 36. Сделаем допущения: 1) Тk, τk – независимые НСВ. 2) Все периоды работы Тk имеют: - законы
- 37. Введём понятие коэффициента готовности Кг(t) Кг(t) – это вероятность того, что в момент времени t объект
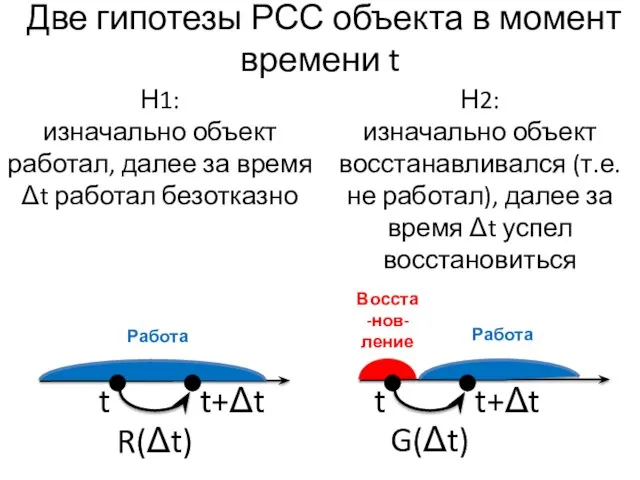
- 38. Две гипотезы РСС объекта в момент времени t t Работа Работа Восста-нов-ление t+Δt t t+Δt Н1:
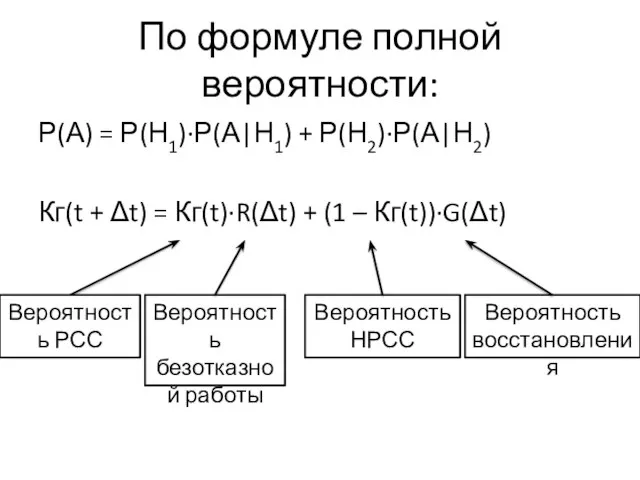
- 39. По формуле полной вероятности: Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2) Кг(t + Δt) = Кг(t)∙R(Δt) + (1
- 40. В разделе 3.1 доказано, что: R(Δt) = 1 – λΔt; G(Δt) = μΔt. Подставим:
- 41. Статистически:
- 42. Коэффициент неготовности – вероятность нахождения объекта в НРСС. Кнг = 1 – Кг Кнг(0) = 0
- 43. Глава 4. Вероятностные модели для расчёта надёжности 4.1. Общие положения Система состоит из множества элементов. Надёжность
- 44. Введем обозначения Аi – событие безотказной работы i-го элемента; Аi – событие отказа i-го элемента; Ас
- 45. Системы отображаются в виде: физических схем: они имеют действительные, электрические связи; логических (расчётных) схем: они отражают
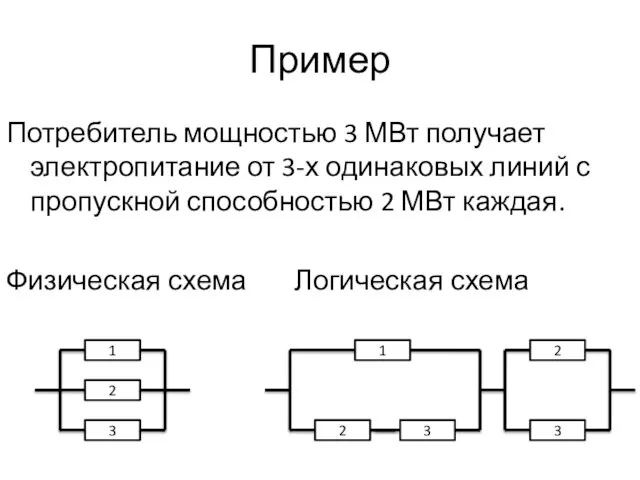
- 46. Пример Потребитель мощностью 3 МВт получает электропитание от 3-х одинаковых линий с пропускной способностью 2 МВт
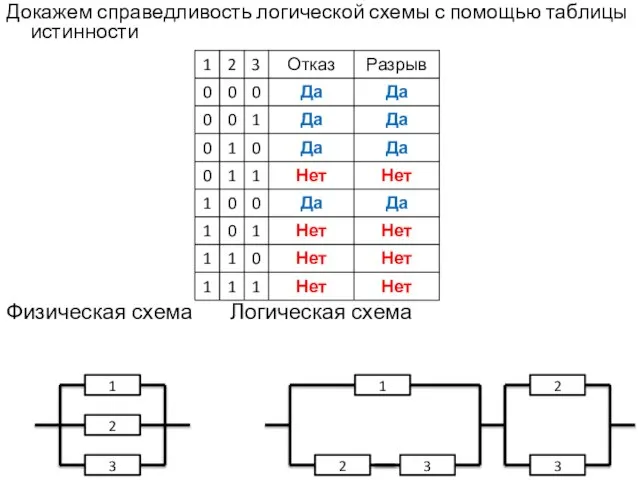
- 47. Докажем справедливость логической схемы с помощью таблицы истинности Физическая схема Логическая схема 1 2 3 1
- 48. 4.2. Последовательное соединение элементов Последовательным (в смысле надёжности) называют такое соединение, при котором отказ одного элемента
- 49. 4.2.1. При отсутствии восстановления элементов Вероятность б.о.р. системы, состоящей из независимых и невосстанавливаемых элементов в течение
- 50. С другой стороны Rс(t) = exp(– λсt) Значит λс = λ1 + λ2 + … +
- 51. 4.2.2. При мгновенном восстановлении элементов Число отказов системы равно сумме чисел отказов элементов. Допустим, за время
- 52. ––––x––––––––––x–––––––x––––––––––––––– 1 эл. ––––––––x–––––––––––––––x–––––––––––––– 2 эл. –––––x–––––––––––––––––––––––––––x––––– 3 эл. ––––––––––x–––––––––––––––––––––x–––––– 4 эл. ––––хх––х–x––––х––––––––хх–––––––xх––––– Система hс =
- 53. Вероятность появления k отказов на интервале Δt: Вероятность б.о.р. системы: R(t) = exp(– λсt) = exp(–
- 54. 4.2.3. При конечном времени восстановления В этом случае при отказе элемента, на время его восстановления отключается
- 55. Дано: последовательность средних периодов б.о.р. элементов: Т1, Т2, …; со средним временем б.о.р. системы: Тс =
- 56. Решение Вероятность отказа i-го элемента на отрезке Δt: λi Δt Вероятность отказа системы на отрезке Δt:
- 58. Формулы для средней длительности восстановления системы
- 59. Выведем коэффициент готовности системы через Тi, τi
- 60. Коэффициент готовности системы
- 61. 4.3. Параллельное соединение элементов 4.3.1. Резервирование одного элемента (n-1) резервным Система с параллельным ( в смысле
- 62. Вероятность отказа такой системы равна: Р(Ас) = Р(А1) ∙ Р(А2) ∙ … ∙ Р(Аn) (при этом
- 63. При равнонадежных элементах и экспоненциаль-ном законе: Qс(t) = (1 – exp(– λt))n, где λ – частота
- 64. При n → ∞ Тс = ln(n)/λ Например: n = 100: Тс = 4,6/λ n =
- 65. Тс = Т / nτn-1 ; τс = τ / n ; λс = nλ /
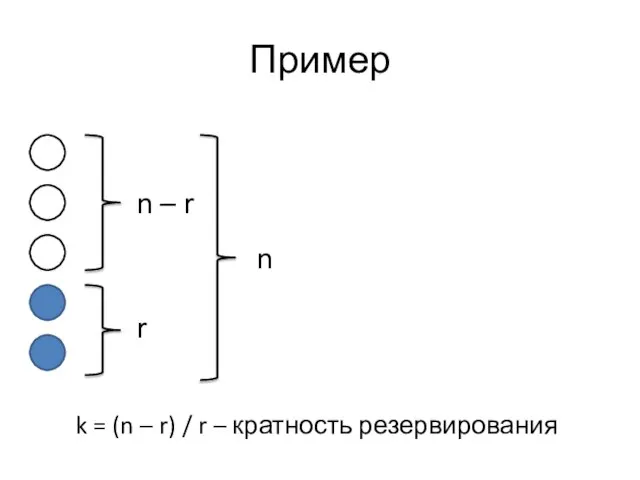
- 66. 4.3.2. Резервирование r рабочих элементов (n – r) резервными Пусть система состоит из n элементов. Пусть
- 67. Пример k = (n – r) / r – кратность резервирования n – r r n
- 68. Как рассчитать функции надежности Rc и отказа Qс всей системы, зная Ri и Qi каждого элемента?
- 69. Пример Дано: Найти: n = 5 Rc r = 2 Qc n – r + 1
- 70. Решение Очевидно, что для системы: Rc + Qc = 1 и для каждого элемента: R +
- 71. Обобщим результаты этого примера
- 72. Виды резервирования По способу включения резервных элементов резервирование бывает: постоянное (резервные объекты включены в систему в
- 73. Постоянное резервирование (неявное) Отказавший элемент должен отключаться защитной аппаратурой, надёжность которой будет определять надёжность всей схемы.
- 74. Резервирование замещением (явное) Отказавший элемент должен отключаться защитной аппаратурой, а резервный элемент должен включаться аппаратурой автоматики.
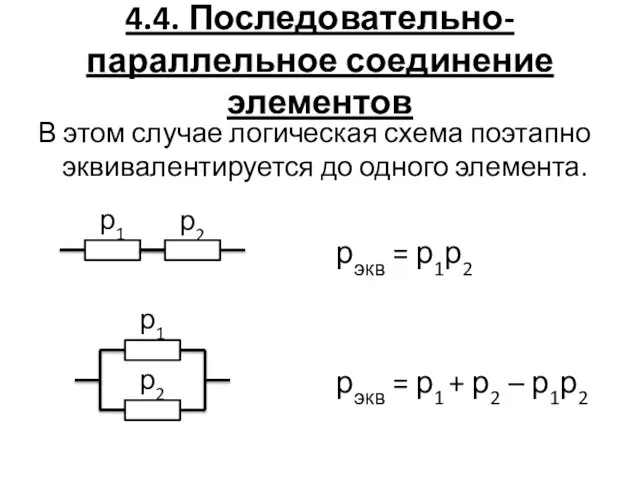
- 75. 4.4. Последовательно-параллельное соединение элементов В этом случае логическая схема поэтапно эквивалентируется до одного элемента. р1 р2
- 76. Полезно помнить, что: при последовательном соединении робщ меньше меньшего; при параллельном соединении робщ больше большего, но
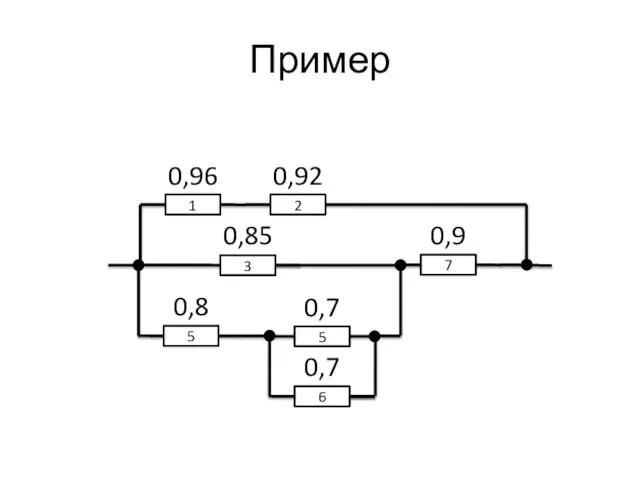
- 77. Пример 1 2 0,96 0,92 3 0,85 5 0,8 5 0,7 6 0,7 7 0,9
- 79. Вывод За счёт параллельных связей надёжность системы выше надёжности каждого элемента.
- 80. 4.5. Метод минимальных путей и сечений Этот метод применяют, когда структуру системы нельзя свести к последовательно-параллельным
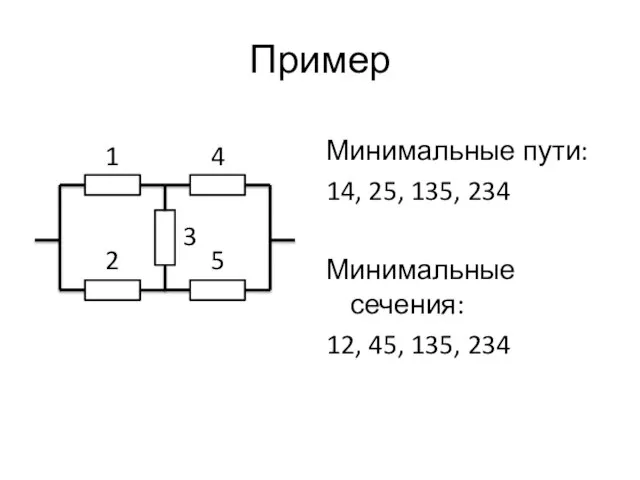
- 81. Минимальный путь – путь, удаление из которого хотя бы одного элемента приводит к тому, что оставшееся
- 82. Пример Минимальные пути: 14, 25, 135, 234 Минимальные сечения: 12, 45, 135, 234 1 2 4
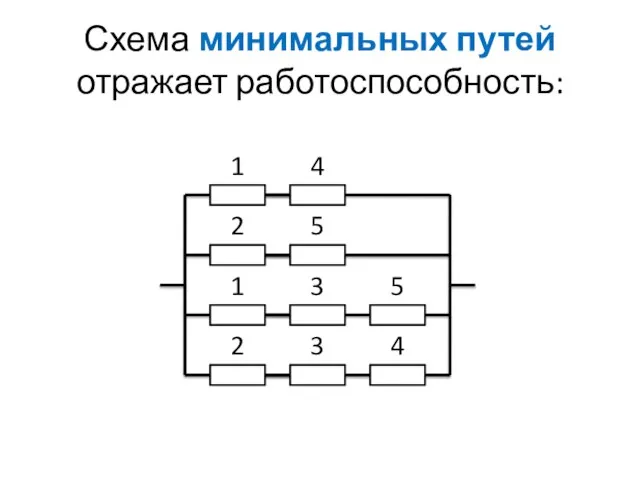
- 83. Схема минимальных путей отражает работоспособность: 1 4 2 5 1 3 2 3 5 4
- 85. Скачать презентацию




![Интенсивность отказов λ(t) [λ] = с-1, ч-1, год-1 и т. д. Статистически:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/365446/slide-11.jpg)








































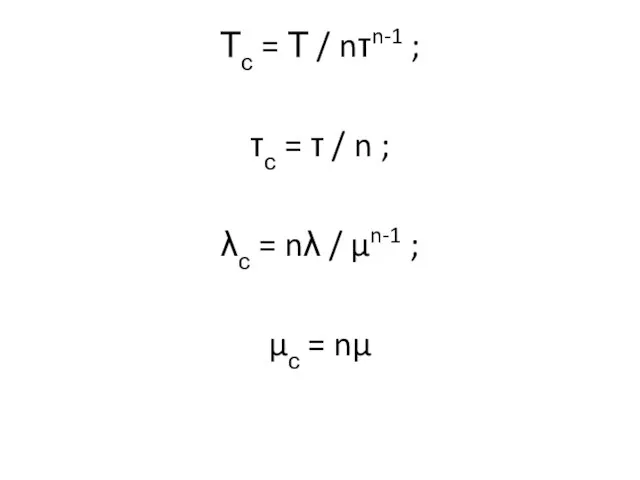













 Диана Торопова Менеджер отдела развития международного бизнеса
Диана Торопова Менеджер отдела развития международного бизнеса Испытание и обеспечение надежности авиационных ГТД
Испытание и обеспечение надежности авиационных ГТД Выход из тупика. Что делать когда уже ничего не хочется и ничего не радует
Выход из тупика. Что делать когда уже ничего не хочется и ничего не радует Подкастинг как новая медиатехнология
Подкастинг как новая медиатехнология Жизнь и быт семейских Забайкалья
Жизнь и быт семейских Забайкалья Предписание. Сущность предписания. Парадоксальное предписание. Прямое предписание
Предписание. Сущность предписания. Парадоксальное предписание. Прямое предписание Презентация НЦЭП
Презентация НЦЭП ГИА 9
ГИА 9 Во главе российского образования
Во главе российского образования Женщины во власти
Женщины во власти Анализ работыМОУ СОШ №2 им. А.С.Пушкина г. МоздокаРСО-Алания за 2007-2008 учебный год
Анализ работыМОУ СОШ №2 им. А.С.Пушкина г. МоздокаРСО-Алания за 2007-2008 учебный год Знакомство с импрессионистами
Знакомство с импрессионистами Настройка пользовательского интерфейса Power Point 2007
Настройка пользовательского интерфейса Power Point 2007 Модель конкурентоспособного выпускника вуза
Модель конкурентоспособного выпускника вуза Презентация на тему Сезонные изменения в природе
Презентация на тему Сезонные изменения в природе  Китайская пейзажная живопись 山水
Китайская пейзажная живопись 山水 Презентация на тему День космонавтики 4 класс
Презентация на тему День космонавтики 4 класс Особенности проведения периодической аккредитации в 2021 году
Особенности проведения периодической аккредитации в 2021 году Процесс Пуассона как универсальный вероятностный процесс для описания изменения параметров в системах взаимодействующих частиц
Процесс Пуассона как универсальный вероятностный процесс для описания изменения параметров в системах взаимодействующих частиц Антимонопольное регулирование цен на нефтепродукты
Антимонопольное регулирование цен на нефтепродукты Психофизиология дошкольников
Психофизиология дошкольников Najpiękniejszy ze wszystkich prezentów
Najpiękniejszy ze wszystkich prezentów Керамогранит. История
Керамогранит. История Темные уголки ЕВРАЗа
Темные уголки ЕВРАЗа Приделы и неопредилености Бураковсая
Приделы и неопредилености Бураковсая "Городской Союз Студенческой Молодежи"
"Городской Союз Студенческой Молодежи" Самые опасные животные
Самые опасные животные Внимание как познавательный процесс
Внимание как познавательный процесс