Содержание
- 2. ЦЕЛЬ УРОКА: рассмотреть задачи Внешнего Независимого оценивания (ЗНО) разных уровней сложности с применением функционально- графических методов
- 3. Задачи урока: повторить свойство монотонности и ограниченности показательной функции; повторить алгоритм построения графиков функции с помощью
- 4. Показательная функция. По закону показательной функции размножалось бы все живое на Земле, если бы для этого
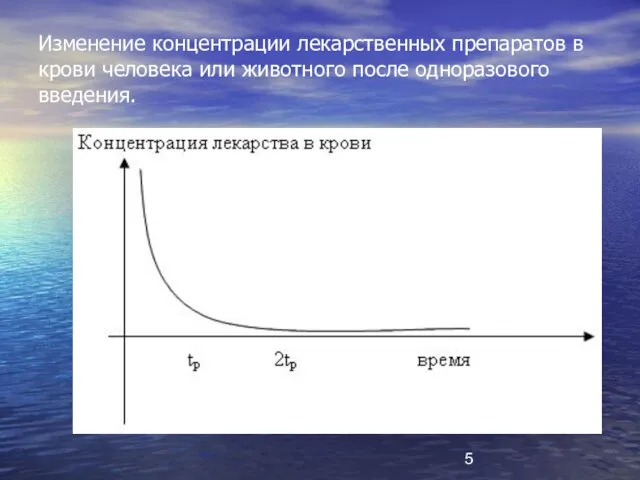
- 5. Изменение концентрации лекарственных препаратов в крови человека или животного после одноразового введения.
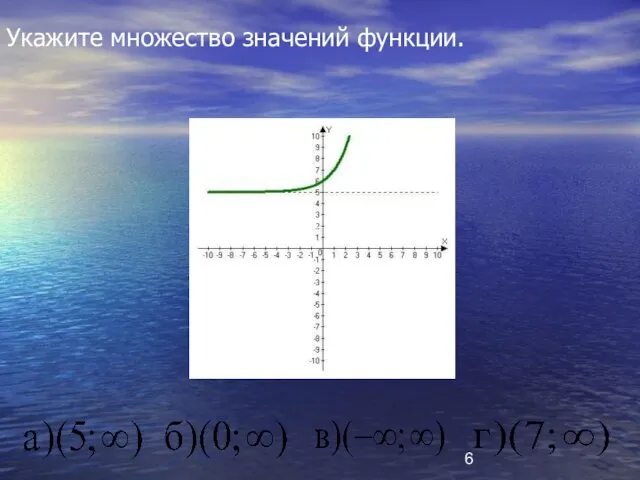
- 6. Укажите множество значений функции. а) (5;
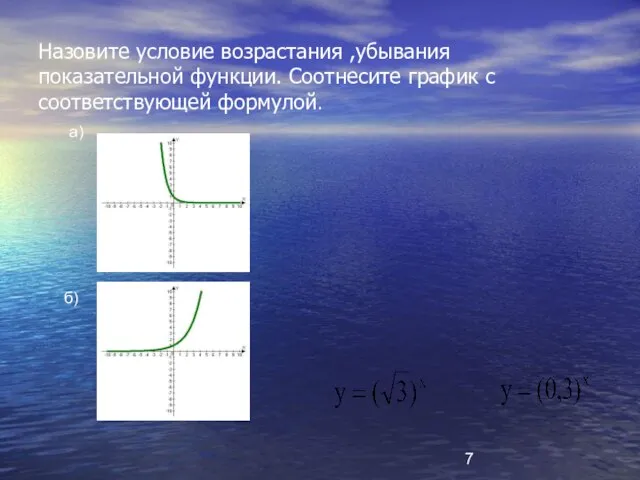
- 7. Назовите условие возрастания ,убывания показательной функции. Соотнесите график с соответствующей формулой. а) б)
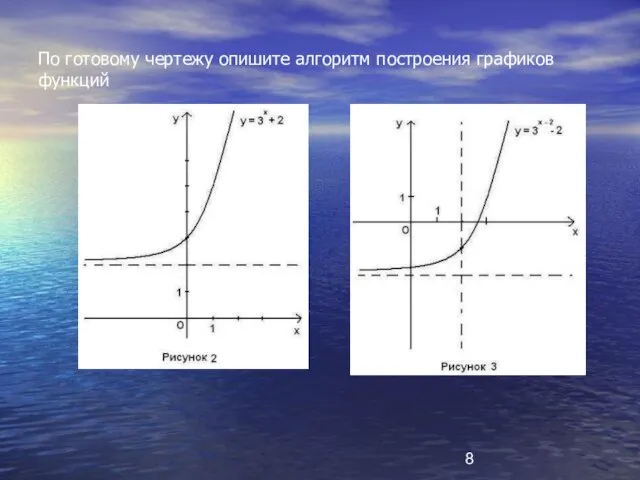
- 8. По готовому чертежу опишите алгоритм построения графиков функций
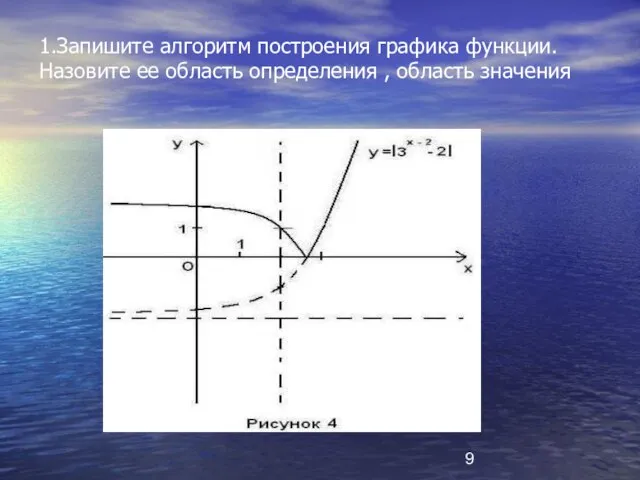
- 9. 1.Запишите алгоритм построения графика функции. Назовите ее область определения , область значения
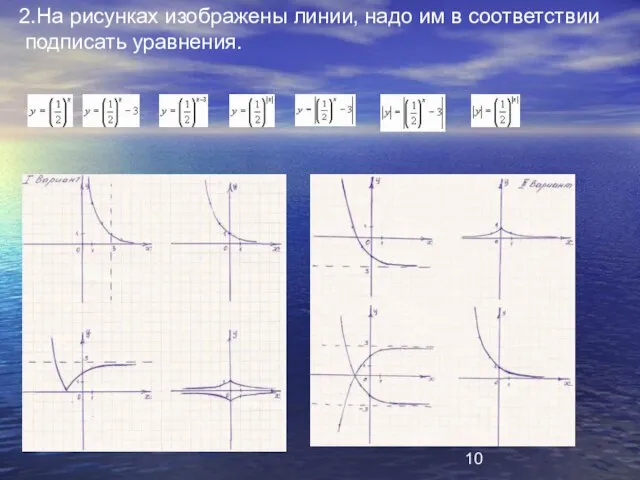
- 10. 2.На рисунках изображены линии, надо им в соответствии подписать уравнения.
- 11. 1. Какая из показательных функций является возрастающей?
- 12. 2.Найти область определения функции:
- 13. 3. Найти область значений функции:
- 14. 4. График функции из графика функции получается А) параллельным переносом вдоль оси Х на 2 единицы
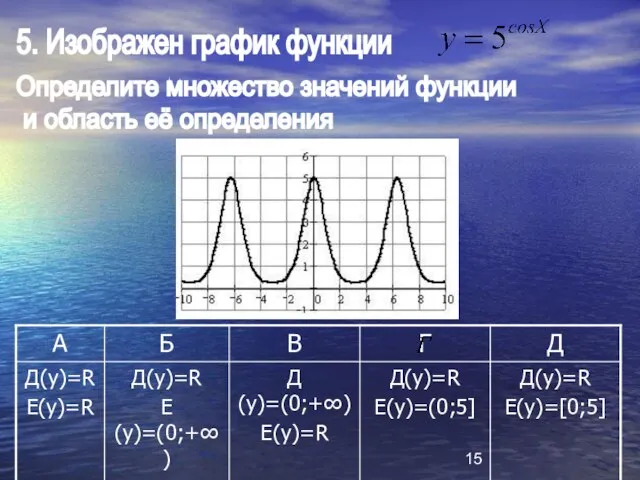
- 15. 5. Изображен график функции Определите множество значений функции и область её определения
- 16. 6. Определите при каком значении a функция проходит через точку Р(2;9)
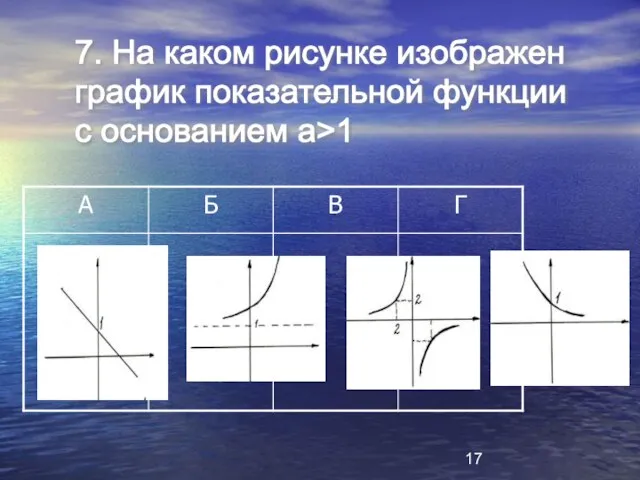
- 17. 7. На каком рисунке изображен график показательной функции с основанием а>1
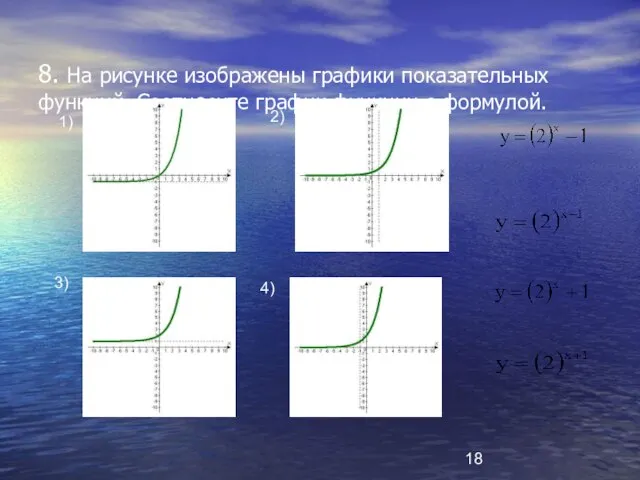
- 18. 8. На рисунке изображены графики показательных функций. Соотнесите график функции с формулой. 1) 2) 3) 4)
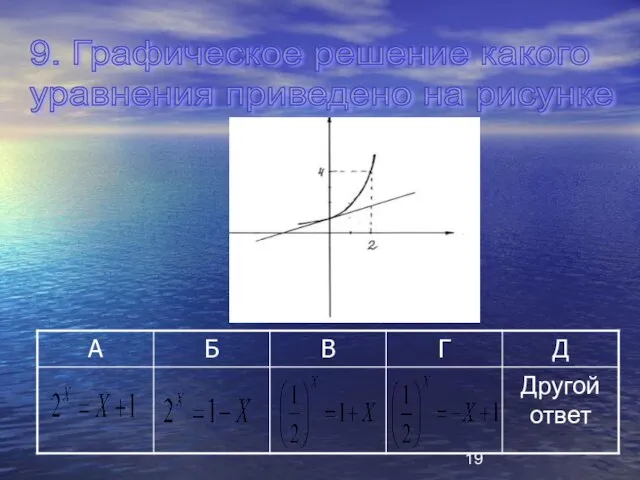
- 19. 9. Графическое решение какого уравнения приведено на рисунке
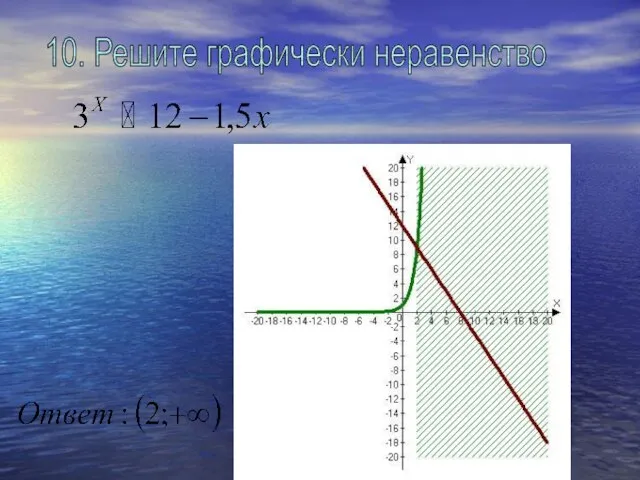
- 20. 10. Решите графически неравенство
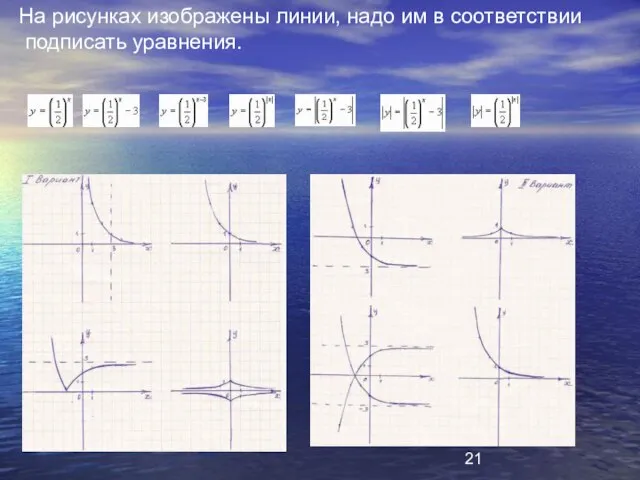
- 21. На рисунках изображены линии, надо им в соответствии подписать уравнения.
- 22. КАК РЕШИТЬ УРАВНЕНИЕ ВИДА: f(x)= g(x)?
- 23. Функционально-графический метод Чтобы решить уравнение вида f(x)= g(x) функционально-графическим методом нужно: Построить графики функций у =
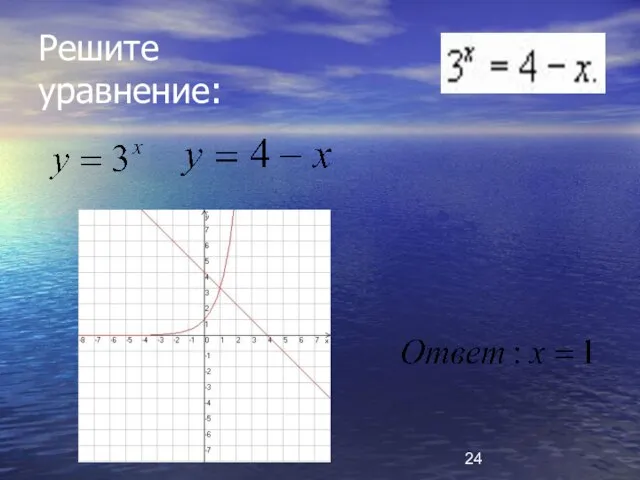
- 24. Решите уравнение:
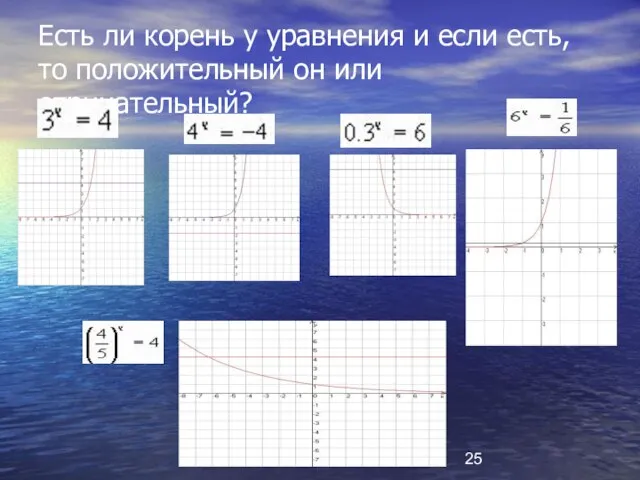
- 25. Есть ли корень у уравнения и если есть, то положительный он или отрицательный?
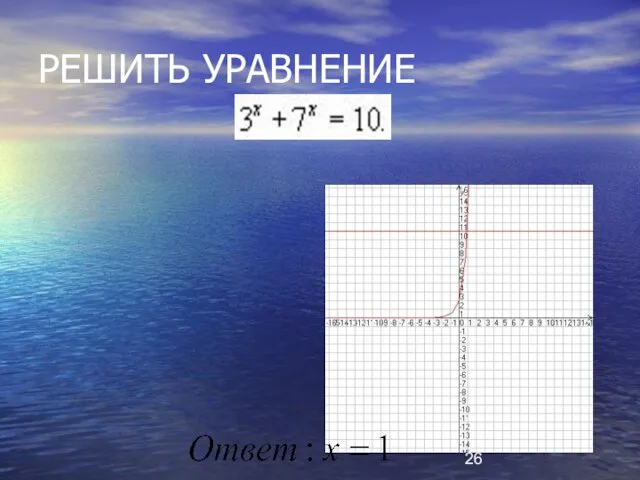
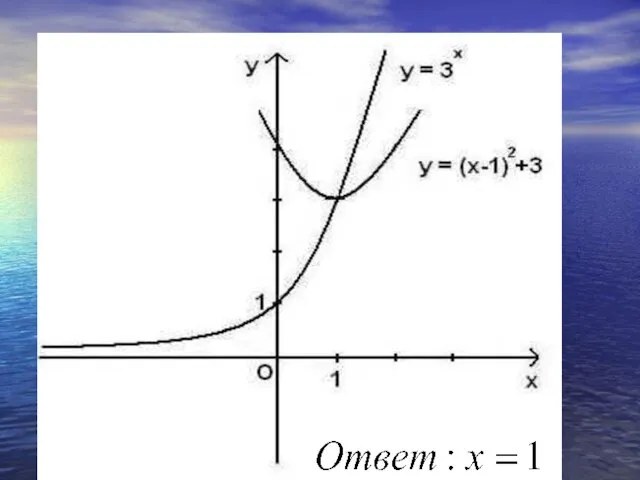
- 26. РЕШИТЬ УРАВНЕНИЕ
- 27. Практическая работа
- 28. . Решите уравнения: 2.Решить неравенство 4.Найдите область значений функции 3.Найти значение выражения ,если ( ; )
- 29. РЕШИТЬ УРАВНЕНИЕ
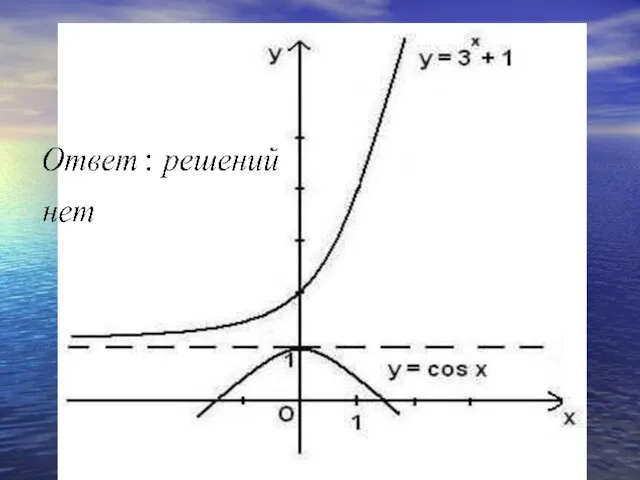
- 31. РЕШИТЬ УРАВНЕНИЕ Решая эту систему, находим, что х = 0.
- 32. Решить неравенство
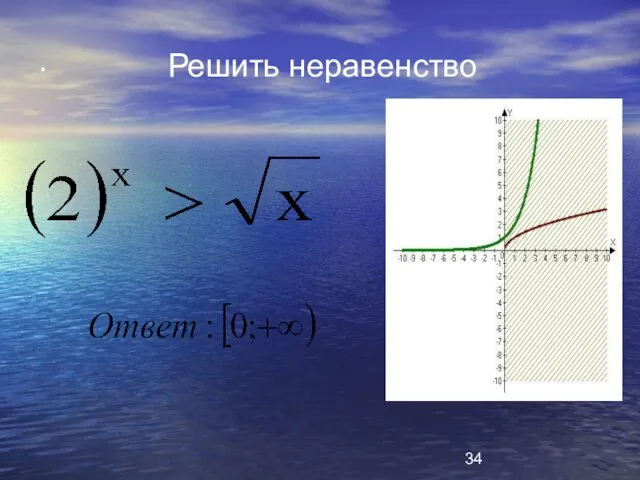
- 34. . Решить неравенство
- 35. Решаем систему уравнений
- 36. Решаем систему уравнений:
- 37. Найти значение выражения , если ( ; ) является решением системы уравнений. Ответ: 0.
- 38. Домашнее задание: Решить графически систему уравнений. Решите уравнение Решите неравенство
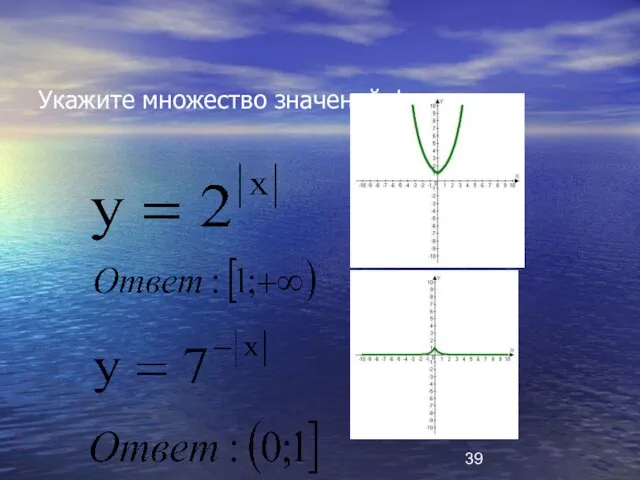
- 39. Укажите множество значений функции
- 40. Найти область значений функции
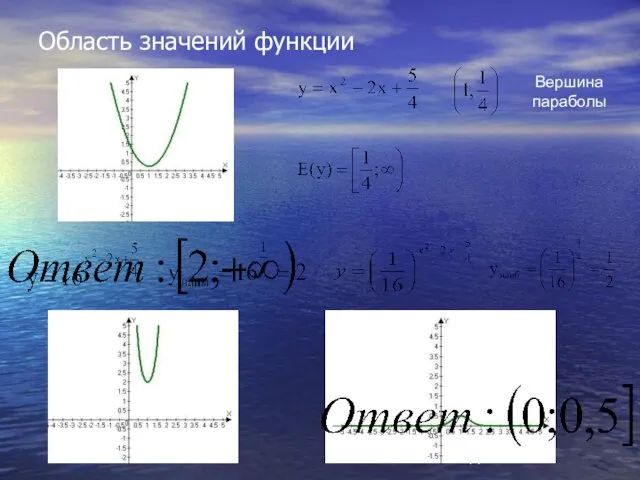
- 41. Область значений функции Вершина параболы
- 42. При каких значениях параметра а уравнение имеет нечетное количество корней?
- 43. Так как график четной функции симметричен относительно оси ординат то если является корнем уравнения, то и
- 44. Решить неравенство Ответ: (- ;2]. Ответ: (-1;0)
- 46. Скачать презентацию








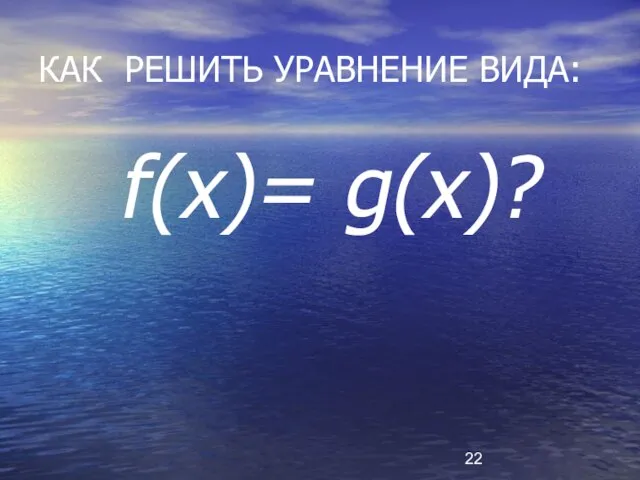



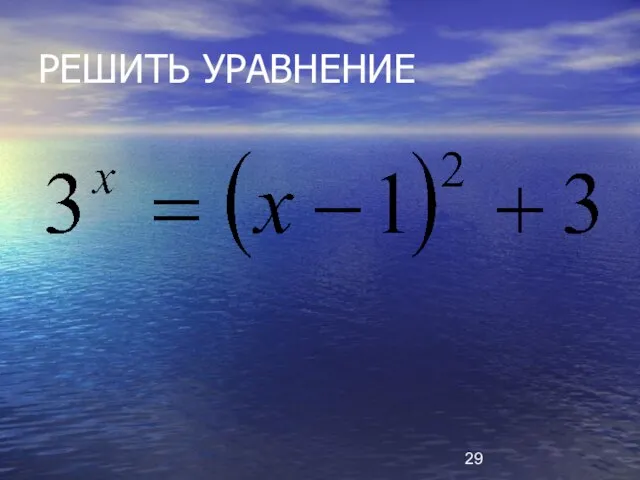









![Решить неравенство Ответ: (- ;2]. Ответ: (-1;0)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/457292/slide-43.jpg)
 New Year Merry Christmas
New Year Merry Christmas Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru
Компания DominiSoft www.dominisoft.ru Компания “БУКА” www.buka.ru www.bukasoft.ru ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ, КАК ВЗАИМОДЕЙСТВИЕ УЧЕНИКА И УЧИТЕЛЯ.
ЗДОРОВЬЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ, КАК ВЗАИМОДЕЙСТВИЕ УЧЕНИКА И УЧИТЕЛЯ. Презентация на тему природа коми края
Презентация на тему природа коми края Синдром эмоционального выгорания
Синдром эмоционального выгорания Система образования и проблемы её структуры
Система образования и проблемы её структуры Волейбол. 5-7 классы
Волейбол. 5-7 классы Война — жесточе нету слова,Война — печальней нету слова. Война — святее нету слова В тоске и славе этих лет.И на устах у нас иного
Война — жесточе нету слова,Война — печальней нету слова. Война — святее нету слова В тоске и славе этих лет.И на устах у нас иного Евгений Львович Шварц (1896-1958)
Евгений Львович Шварц (1896-1958) Водоёмы нашей местности
Водоёмы нашей местности Фармакоэпидемиологические и фармакоэкономические аспекты нежелательных реакций лекарственных препаратов – неявная проблема и
Фармакоэпидемиологические и фармакоэкономические аспекты нежелательных реакций лекарственных препаратов – неявная проблема и  Зиянкестердің экономикалық шекті. Зиянын табиғи жауларының тиімділігінің деңгейін анықтау. (Лекция 15)
Зиянкестердің экономикалық шекті. Зиянын табиғи жауларының тиімділігінің деңгейін анықтау. (Лекция 15) Séjour d’études linguistiques Découverte de la Provence
Séjour d’études linguistiques Découverte de la Provence Символи України. Національний український одяг
Символи України. Національний український одяг Законы развития теории судебной экспертизы
Законы развития теории судебной экспертизы Командный проект. Бизнес-задача
Командный проект. Бизнес-задача Взаимодействие с заинтересованными сторонами при подготовке интегрированных отчетов
Взаимодействие с заинтересованными сторонами при подготовке интегрированных отчетов Экономить - значит зарабатывать! Плакат для рабочих
Экономить - значит зарабатывать! Плакат для рабочих Что такое деятельность
Что такое деятельность Микеланджело
Микеланджело  Лучший центр. Белорецк. Скалодром
Лучший центр. Белорецк. Скалодром Здоровьесберегающие технологии в образовательном процессе. Подготовил: зам.директора по УВР Павлов В.В.
Здоровьесберегающие технологии в образовательном процессе. Подготовил: зам.директора по УВР Павлов В.В. Лекция 5. Проблема психологического контроля и управления спортивной деятельностью
Лекция 5. Проблема психологического контроля и управления спортивной деятельностью Опорные схемы и рисунки в помощь учащимся
Опорные схемы и рисунки в помощь учащимся Топология компьютерных сетей
Топология компьютерных сетей Процессоры фирм Intel и AMD
Процессоры фирм Intel и AMD Стили в одежде
Стили в одежде «1С:Предприятие 8. Управление водоканалом»
«1С:Предприятие 8. Управление водоканалом»