Поле движущихся зарядов

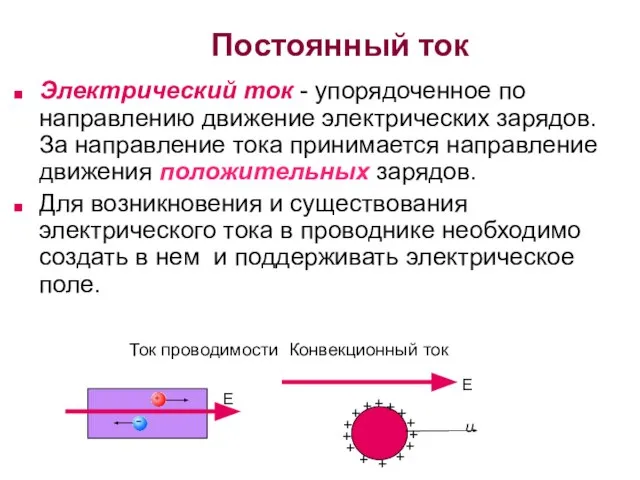
Постоянный ток
Электрический ток - упорядоченное по направлению движение электрических зарядов. За направление тока принимается направление движения положительных зарядов.
Для возникновения и существования электрического тока в проводнике необходимо создать в нем и поддерживать электрическое поле.
E
+
+
+
+
+
+
+
+
+
+
+
+
+
+
υ
Ток проводимости Конвекционный ток

Количественная мера тока
Ток характеризуется силой тока I – скалярной величиной, численно равной количеству переносимого электричества q за единицу времени через поперечное сечение проводника: I=dq/dt.

Сила тока измеряется в амперах:
1А = 1Кл/1с.
Для постоянного тока: I=q/t.
Используется векторная величина – плотность тока: j = I/S,
где S – площадь поперечного
сечения проводника.
Единица плотности тока – ампер на метр в квадрате (А/м2)
Единицы измерения

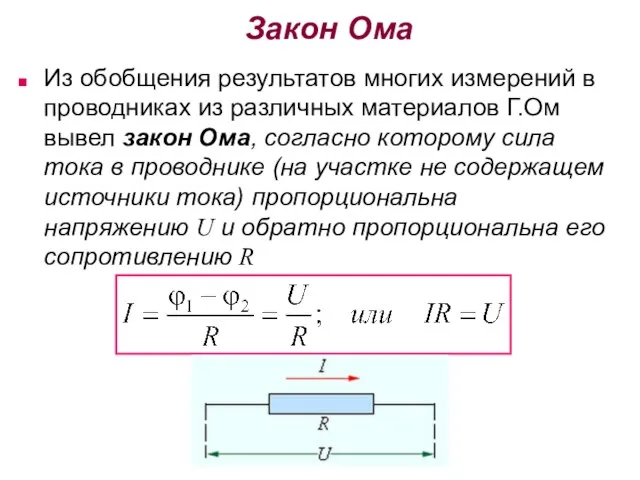
Закон Ома
Из обобщения результатов многих измерений в проводниках из различных материалов Г.Ом вывел закон Ома, согласно которому сила тока в проводнике (на участке не содержащем источники тока) пропорциональна напряжению U и обратно пропорциональна его сопротивлению R

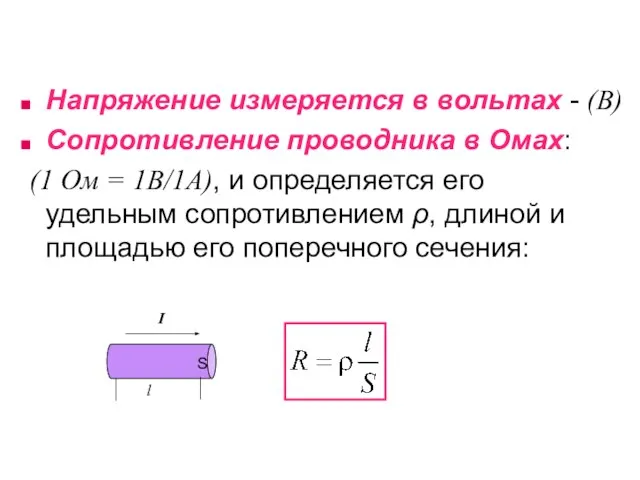
Напряжение измеряется в вольтах - (В)
Сопротивление проводника в Омах:
(1 Ом = 1В/1А), и определяется его удельным сопротивлением ρ, длиной и площадью его поперечного сечения:

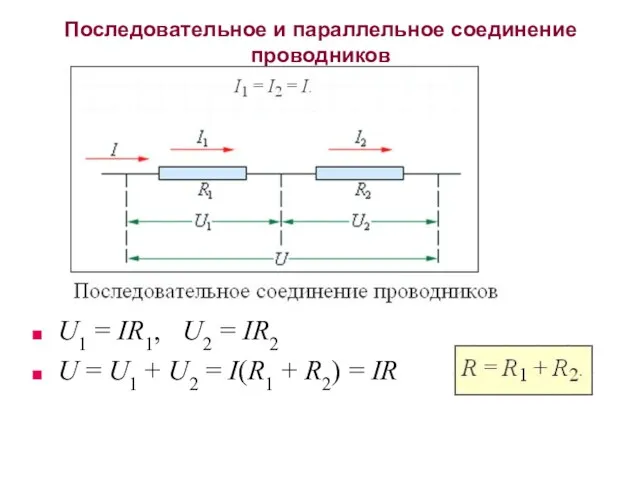
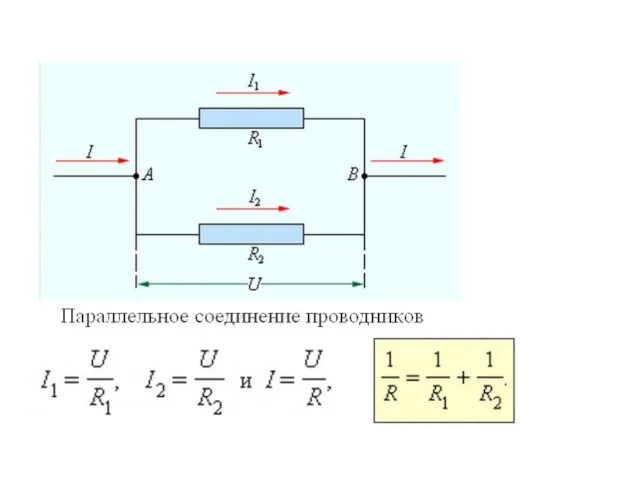
Последовательное и параллельное соединение проводников
U1 = IR1, U2 = IR2
U = U1 + U2 = I(R1 + R2) = IR

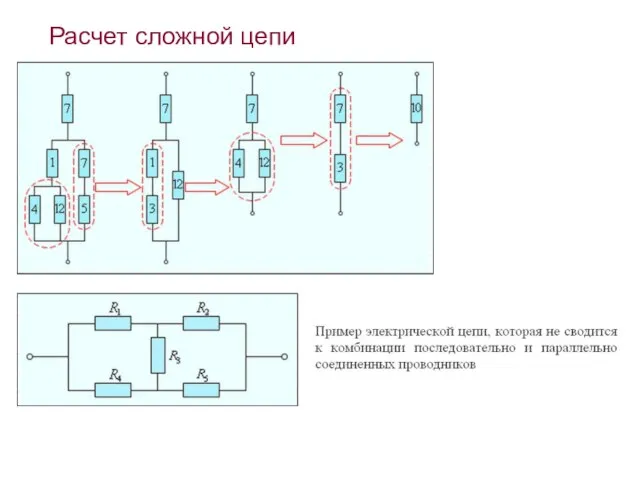
Расчет сложной цепи

Работа тока и мощность тока
Работа тока на участке цепи, совершаемая за время t, определяется как:
A = IUt = I2 Rt = U2t/R.
(1 Дж = 1⋅Н⋅м = 1 м2⋅кг⋅с-2)
Мощность тока на участке цепи равна:
N = A/t = IU = I2R = U2/R.
(1 Вт = 1 Дж/с = 1⋅м2⋅кг⋅с-3)

Закон Джоуля–Ленца
Работа тока проявляется в превращении электрической энергии в механическую (например, в электродвигателе), в химическую (например, при выделении из раствора химически чистого компонента), во внутреннюю (например, при нагревании проводника).
Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике

Сторонние силы.
Для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока.
Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.

Цепь постоянного тока можно разбить на отдельные участки.
Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными.
Участки, включающие источники тока, называются неоднородными.

ЭДС
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда Q0 от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
E
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе , действующей на данном участке.

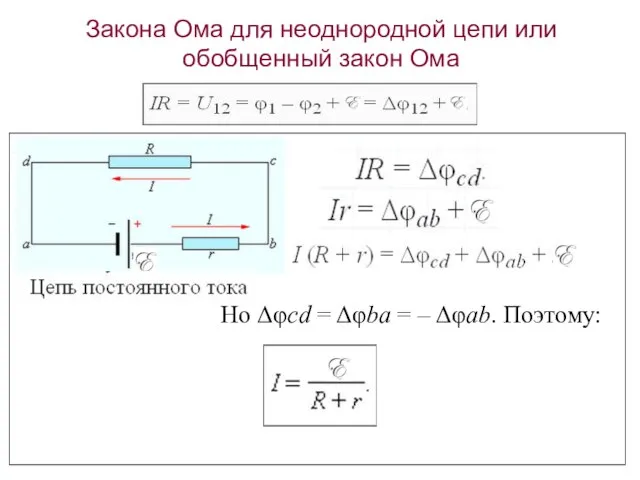
Полная работа на неоднородном участке равна:
Величину U12 принято называть падением напряжения или просто напряжением на участке цепи 1–2
Для однородного участка напряжение равно разности потенциалов:

Но Δφcd = Δφba = – Δφab. Поэтому:
Закона Ома для неоднородной цепи или обобщенный закон Ома

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

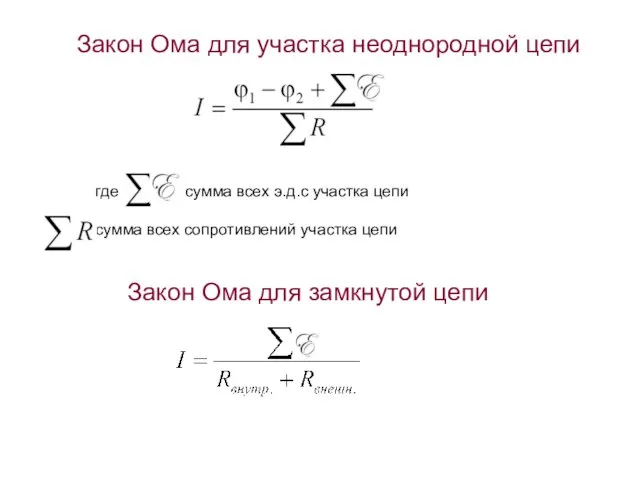
Закон Ома для участка неоднородной цепи
Закон Ома для замкнутой цепи

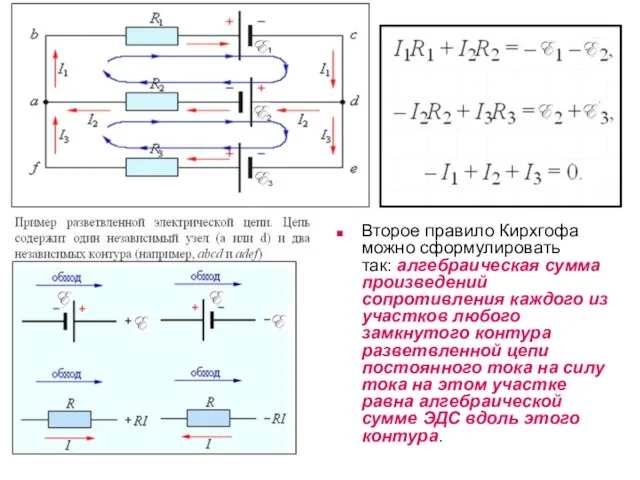
Правила Кирхгофа для разветвленных цепей
Первое правило Кирхгофа гласит, что алгебраическая сумма токов в любом узле любой цепи равна нулю (значения вытекающих токов берутся с обратным знаком):
I1
I2
I3
I1 -I2 - I3 =0

Второе правило Кирхгофа можно сформулировать так: алгебраическая сумма произведений сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока на этом участке равна алгебраической сумме ЭДС вдоль этого контура.

Магнитное поле и его характеристики
Магнитное поле – это поле окружающее токи и постоянные магниты и оказывающее силовое воздействие на проводники с током и на постоянные магниты.
Важной особенностью магнитного поля является то, что оно действует, только на движущиеся в нем электрические заряды.

Вектор магнитной индукции
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции B который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.

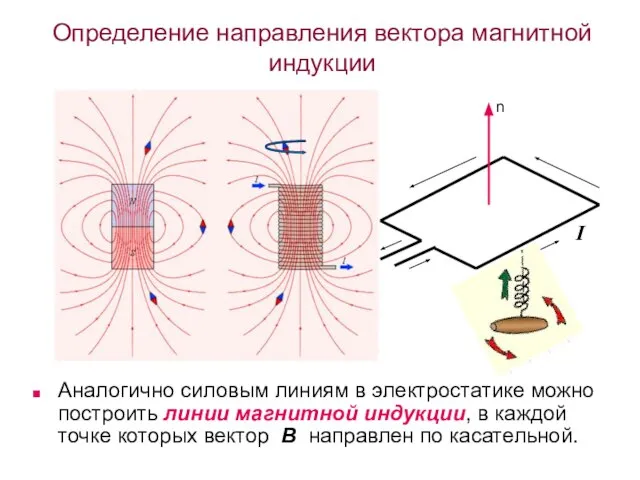
Определение направления вектора магнитной индукции
Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор B направлен по касательной.
n

Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми.
Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

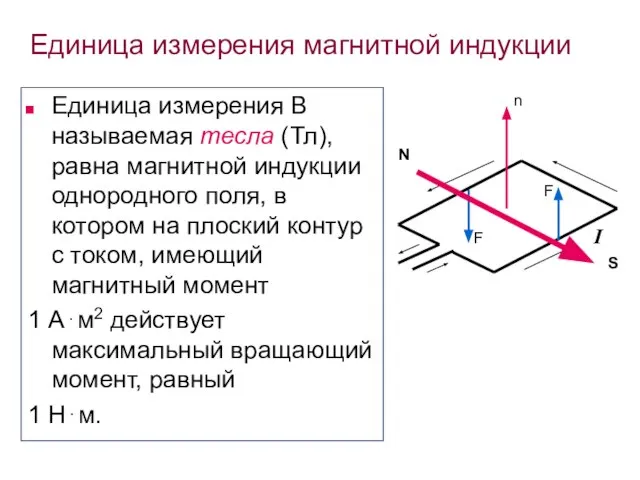
Единица измерения магнитной индукции
Единица измерения B называемая тесла (Тл), равна магнитной индукции однородного поля, в котором на плоский контур с током, имеющий магнитный момент
1 А⋅м2 действует максимальный вращающий момент, равный
1 Н⋅м.

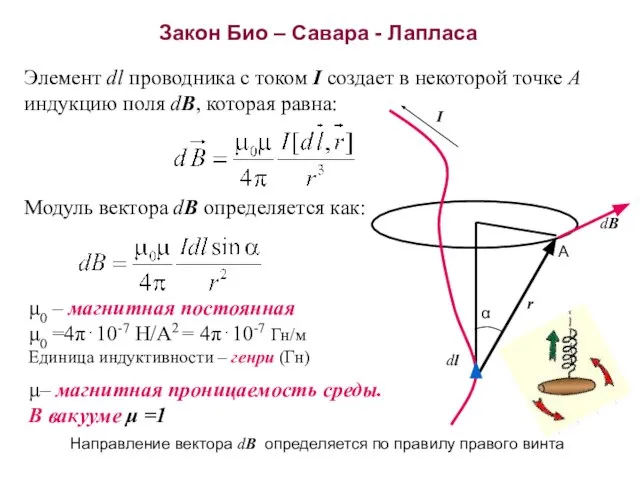
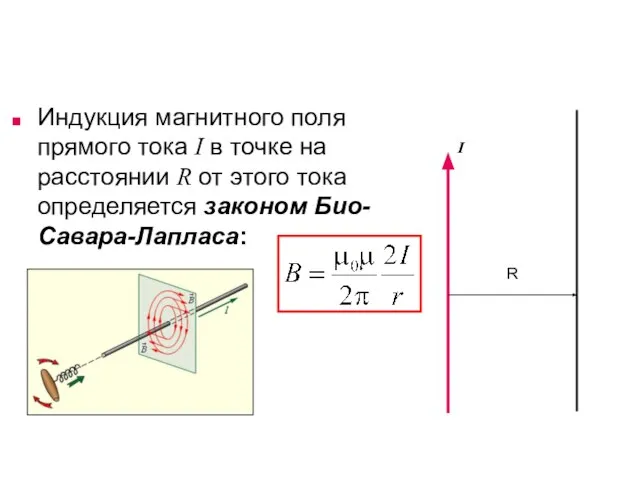
Закон Био – Савара - Лапласа
A
Элемент dl проводника с током I создает в некоторой точке A индукцию поля dB, которая равна:
Модуль вектора dB определяется как:
μ0 – магнитная постоянная
μ0 =4π⋅10-7 Н/А2 = 4π⋅10-7 Гн/м
Единица индуктивности – генри (Гн)
μ– магнитная проницаемость среды.
В вакууме μ =1
Направление вектора dB определяется по правилу правого винта

Индукция магнитного поля прямого тока I в точке на расстоянии R от этого тока определяется законом Био-Савара-Лапласа:
I
R

Напряженность магнитного поля
Векторную величину
Н = В/μμ0, характеризующую зависимость магнитного поля в некоторой точке от силы тока и положения этой точки, называют напряженностью магнитного поля.

Принцип суперпозиции
Вектор магнитной индукции результирующего поля, создаваемого несколькими токами или движущимися зарядами, равен векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или зарядом в отдельности.

Вычисление поля, создаваемого током, текущим по тонкому круговому проводнику

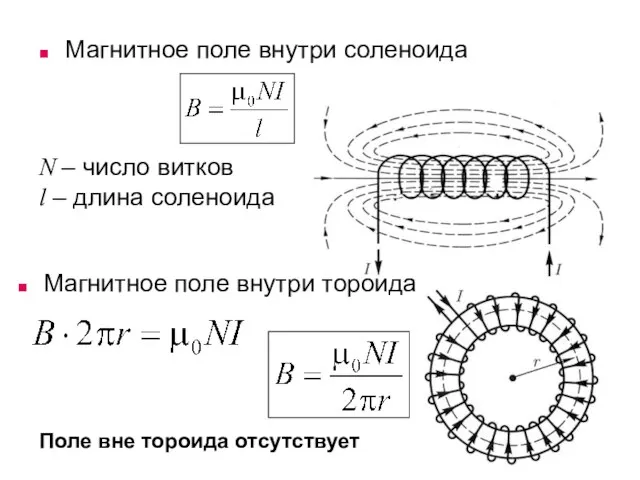
Магнитное поле внутри соленоида
N – число витков
l – длина соленоида
Магнитное поле внутри тороида
Поле вне тороида отсутствует

Закон Ампера.
Движение в магнитном поле проводника (элемента длиной dl) с током определяется силой Ампера:
dF= I[dl,В].
Модуль силы вычисляется по формуле:
dF =IBdl⋅sinα
Для определения направления силы Ампера используют правило левой руки: если расположить ее так, чтобы линии индукции В входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник.

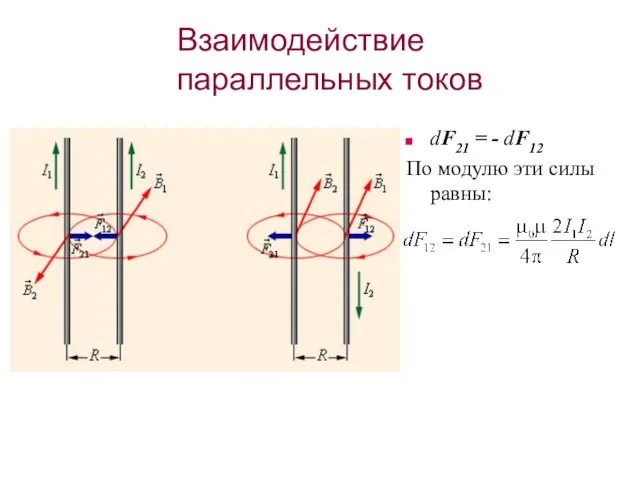
Взаимодействие параллельных токов
dF21 = - dF12
По модулю эти силы равны:

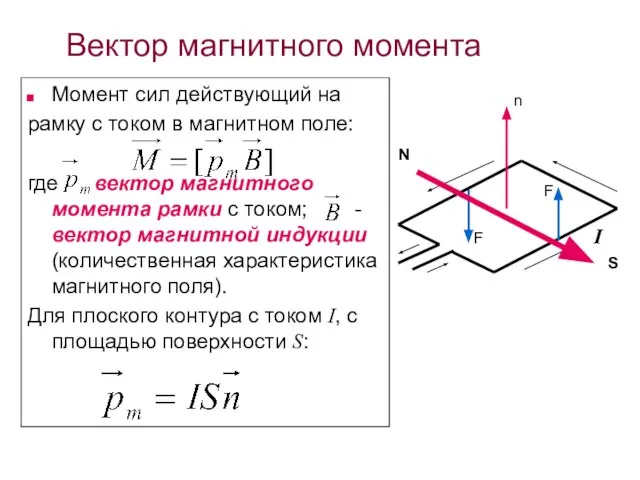
Вектор магнитного момента
Момент сил действующий на
рамку с током в магнитном поле:
где вектор магнитного момента рамки с током; - вектор магнитной индукции (количественная характеристика магнитного поля).
Для плоского контура с током I, с площадью поверхности S:

Магнитный момент характеризует магнитные свойства контура с током. Поскольку М/I = ВS, а В определяет плотность линий магнитной индукции, то произведение ВS соответствует количеству линий, пронизывающих контур рамки, и всю совокупность линий называют магнитным потоком Ф сквозь этот контур. Выходящие линии считают со знаком «плюс», а входящие – «минус».

Поток вектора магнитной индукции. Теорема Гаусса для поля B
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная
Для произвольной
поверхности S
Если B ⊥ S
ΦB = BS

Единица магнитного потока
Единица магнитного потока вебер (Вб)
1 Вб магнитный поток, проходящий сквозь плоскую поверхность 1 м2, расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.
1 Вб = 1 Тл⋅м2

Теорема Гаусса для поля B
Поток вектора магнитной индукции через замкнутую поверхность равен нулю:
Эта теорема отражает отсутствие магнитных зарядов и то, что линии магнитной индукции являются замкнутыми (не имеют ни начала, ни конца.

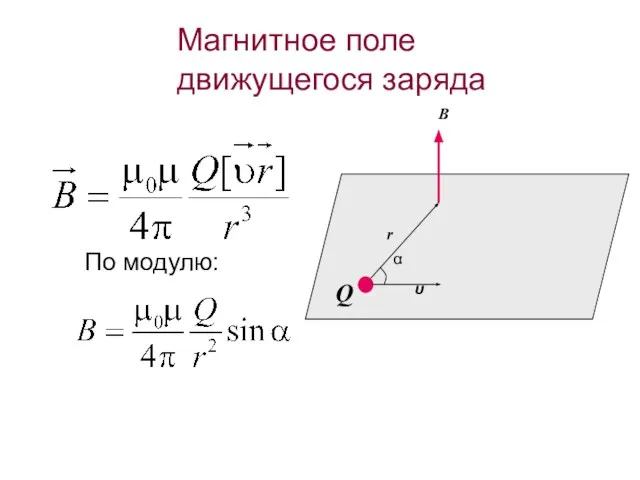
Магнитное поле движущегося заряда
По модулю:
Q

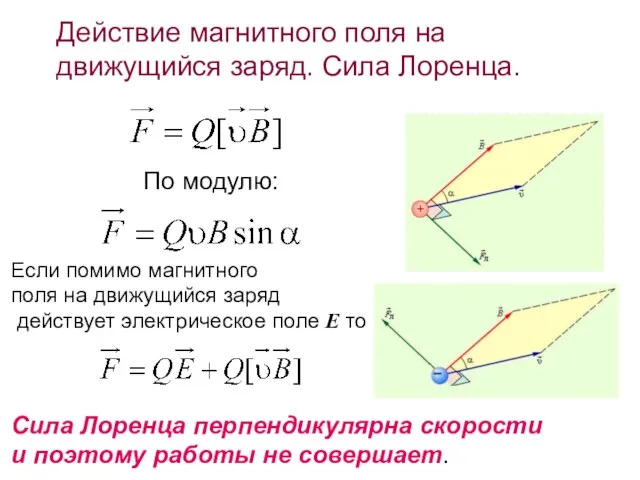
Если помимо магнитного
поля на движущийся заряд
действует электрическое поле E то
Действие магнитного поля на движущийся заряд. Сила Лоренца.
По модулю:
Сила Лоренца перпендикулярна скорости
и поэтому работы не совершает.

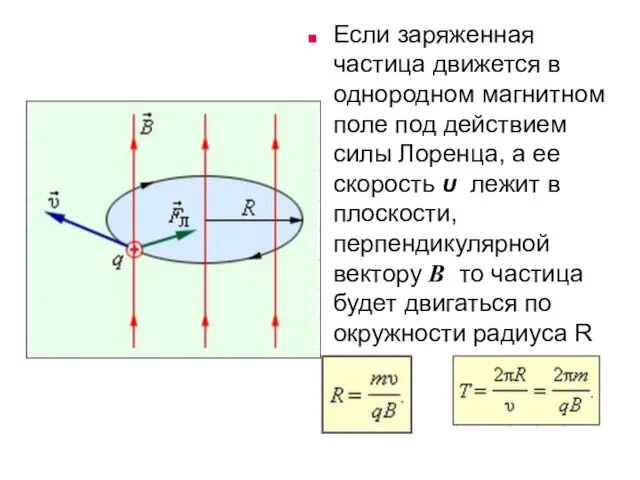
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость υ лежит в плоскости, перпендикулярной вектору B то частица будет двигаться по окружности радиуса R

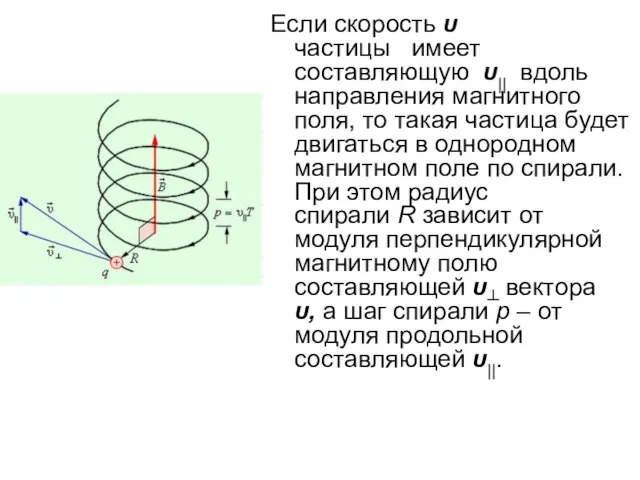
Если скорость υ частицы имеет составляющую υ|| вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора υ, а шаг спирали p – от модуля продольной составляющей υ||.

Циркуляция вектора B магнитного поля в вакууме
Циркуляцией вектора B по заданному замкнутому контуру называется интеграл

Теорема о циркуляции вектора B
Закон полного тока для магнитного поля в вакууме:
Циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, охватываемых этим контуром:
I1

Если циркуляция вектора E электростатического поля равна 0, т.е электростатическое поле является потенциальным, то циркуляция вектора B не равна 0 и такое поле называется вихревым.