Понятие многогранников и их виды…

Цели работы:
Познакомиться с многогранниками.
Показать влияние правильных многогранников на возникновение философских теорий и гипотез.
Показать связь геометрии и природы.
Познакомиться с примерами применения многогранников в архитектуре и искусстве.

Содержание:
Многогранники в природе.
Историческая справка.
Многогранники в искусстве.
Многогранники в архитектуре.

Многогранник - часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника, причем вокруг каждой вершины существует ровно один цикл многоугольников

Многогранник называется правильным, если все его грани – равные правильные многогранники и в каждой его вершине сходится одно и то же число ребер.

Тетраэдр
Тетраэдр составлен из 4-х равносторонних треугольников. Каждая вершина является вершиной 3-х треугольников.

Октаэдр
Октаэдр составлен из 8 равносторонних треугольников. Каждая вершина октаэдра является вершиной 4-х треугольников.

Икосаэдр
Икосаэдр составлен из 20 равносторонних треугольников. Каждая вершина икосаэдра является вершиной 5 треугольников

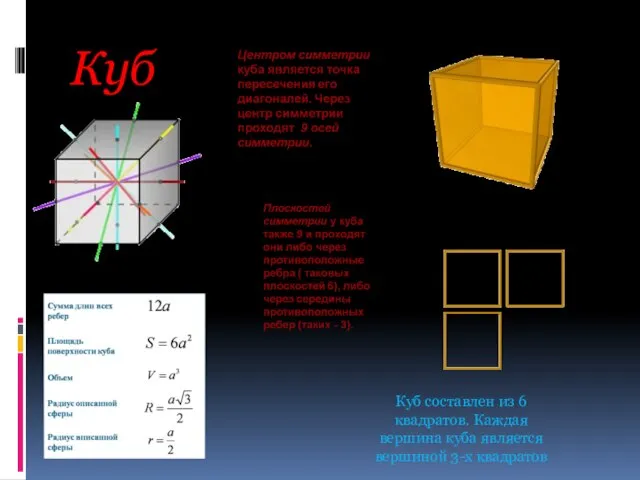
Куб
Куб составлен из 6 квадратов. Каждая вершина куба является вершиной 3-х квадратов

Додекаэдр
Додекаэдр составлен из 12 правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.

Многогранники в природе
"Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".

Чудо природы – кристаллы
куб передает форму кристаллов поваренной соли NaCl
монокристалл алюминиево-калиевых квасцов имеет форму октаэдра,
кристалл сернистого колчедана FeS имеет форму додекаэдра,
сернокислый натрий - тетраэдр,
бор - икосаэдр.

шеелит
Гранаты: Андрадит и Гроссуляр
Дуза кристаллов дворца

Историческая справка
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.
История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы

Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
Существование пяти правильных многогранников они относили к строению материи и Вселенной.
Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел:

Дальнейшее развитие математики связано с именами
Платона, Евклида, Архимеда, Кеплера
Все использовали в своих философских теориях
правильные многогранники.

Многогранники в искусстве
«Поистине, живопись — наука и законная дочь природы,
ибо она порождена природой»
(Леонардо да Винчи)

Знаменитый художник, увлекавшийся геометрией,
Альбрехт Дюрер
(1471- 1528),
в известной гравюре «Меланхолия»
на переднем плане
изобразил додекаэдр.

Пример изображения правильных многогранников, выполненный художником 20 века Сальвадором Дали
Картина «Тайная вечерня». Христос со своими учениками изображен на фоне огромного прозрачного додекаэдра. Форму додекаэдра, по мнения древних, имела ВСЕЛЕННАЯ, т.е. они считали, что мы живем внутри свода, имеющего форму поверхности додекаэдра.

Многогранники в архитектуре
Казанская церковь в Москве
Собор непорочного зачатия Девы Марии

Исторический музей
ЦУМ

«Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!»

Литература:
- Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
- Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.
- Ворошилов А.В. Математика и искусство. - М. просвещение, 1992. – 352
- Рыбников К.А. История математики: Учебник. - М.: Изд-во МГУ, 1994. - 495 с