Содержание
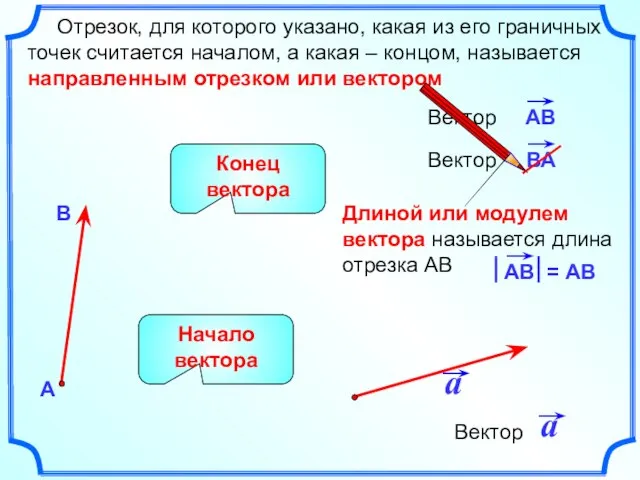
- 2. Длиной или модулем вектора называется длина отрезка АВ Отрезок, для которого указано, какая из его граничных
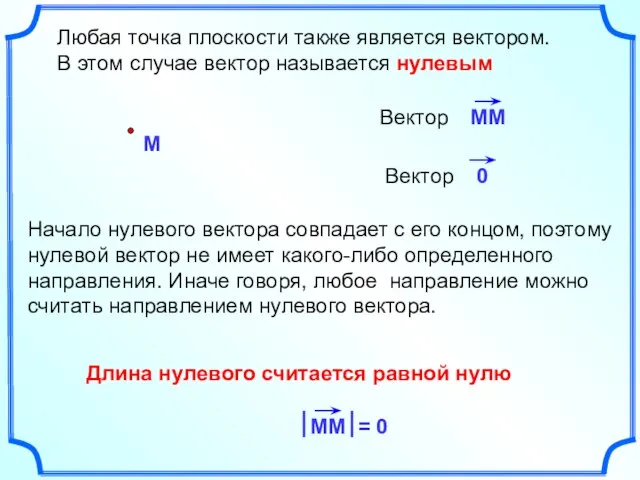
- 3. Любая точка плоскости также является вектором. В этом случае вектор называется нулевым Длина нулевого считается равной
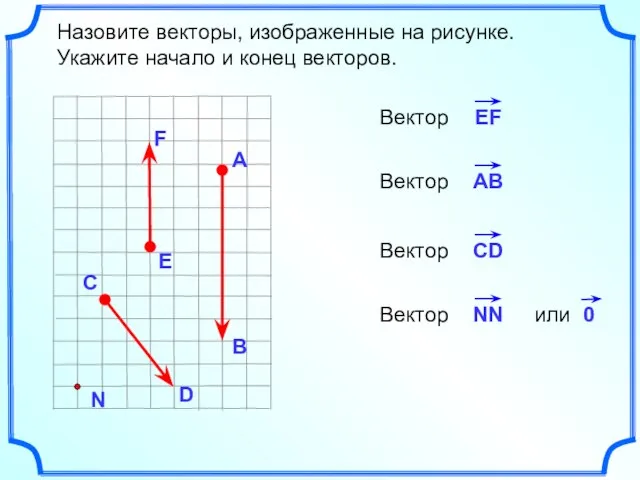
- 4. Назовите векторы, изображенные на рисунке. Укажите начало и конец векторов.
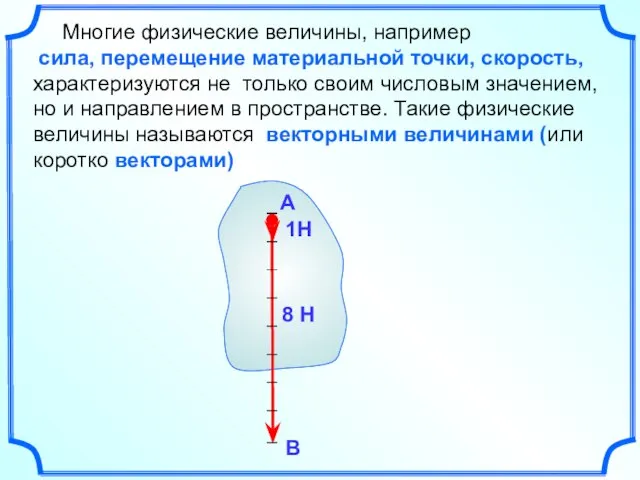
- 5. Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но
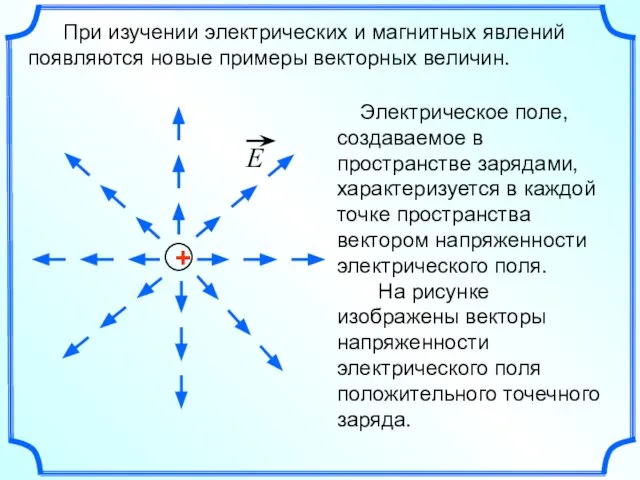
- 6. При изучении электрических и магнитных явлений появляются новые примеры векторных величин.
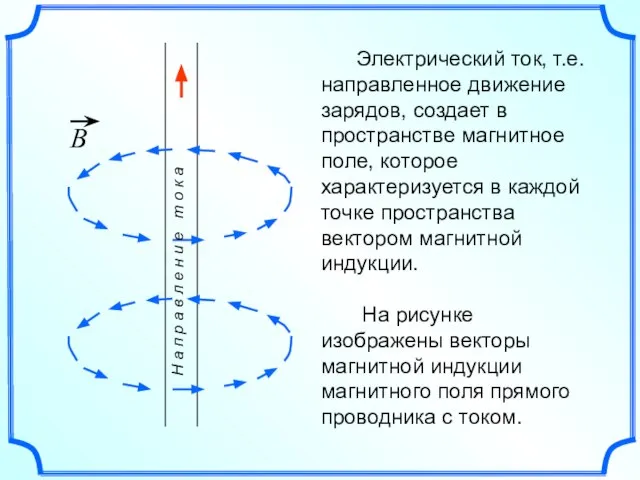
- 7. Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке
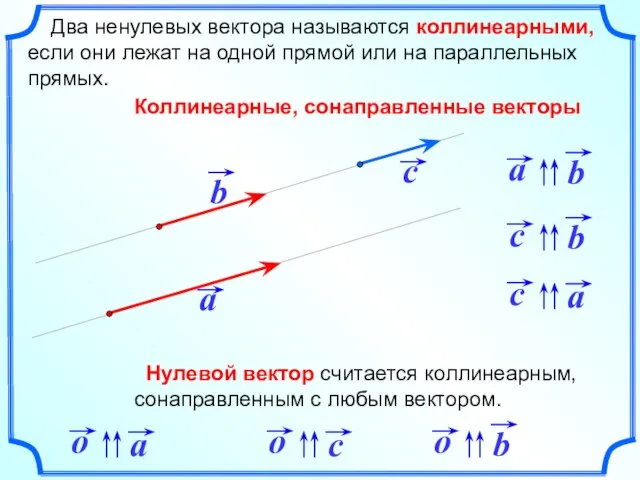
- 8. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
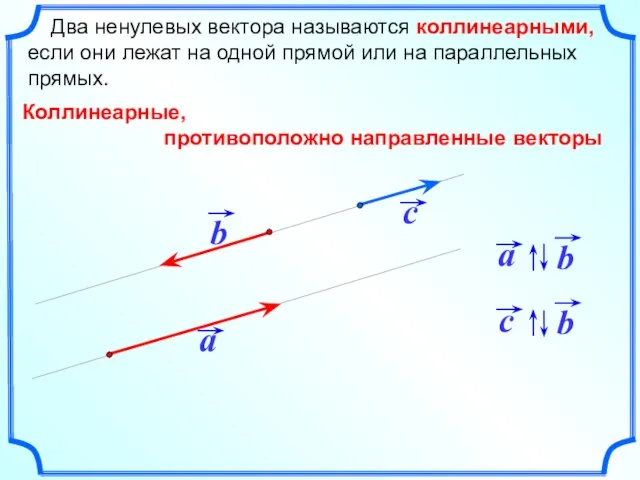
- 9. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные,
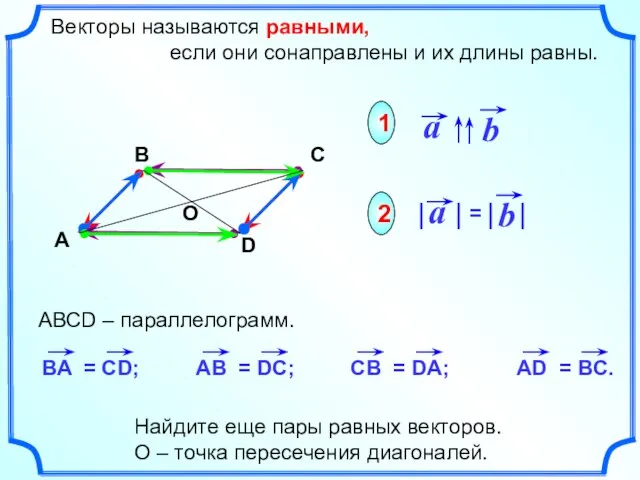
- 10. Векторы называются равными, если они сонаправлены и их длины равны. 1 2 Найдите еще пары равных
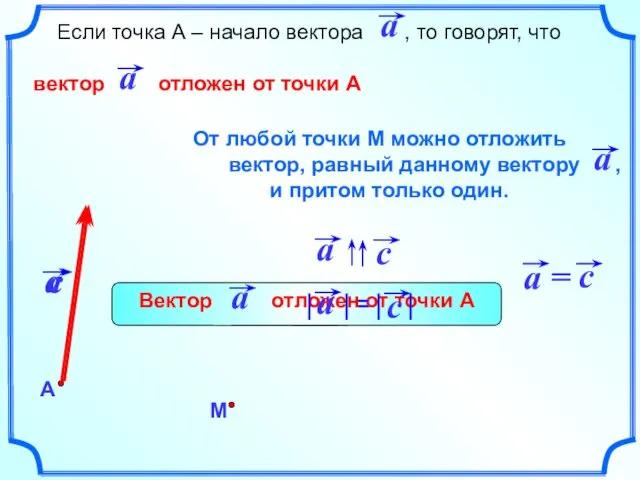
- 11. Если точка А – начало вектора , то говорят, что вектор отложен от точки А
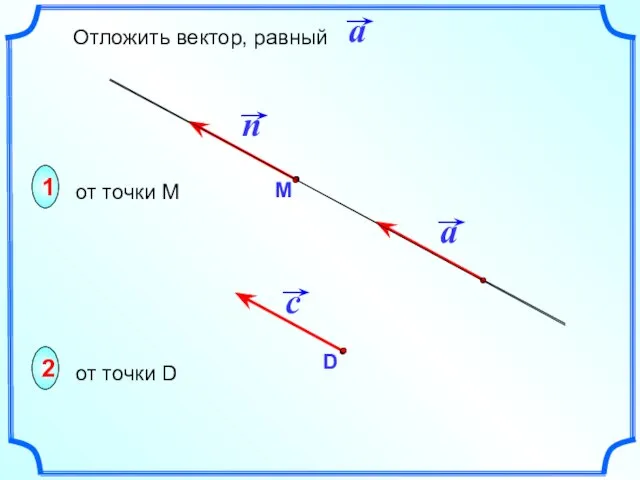
- 12. 1 2 от точки М от точки D
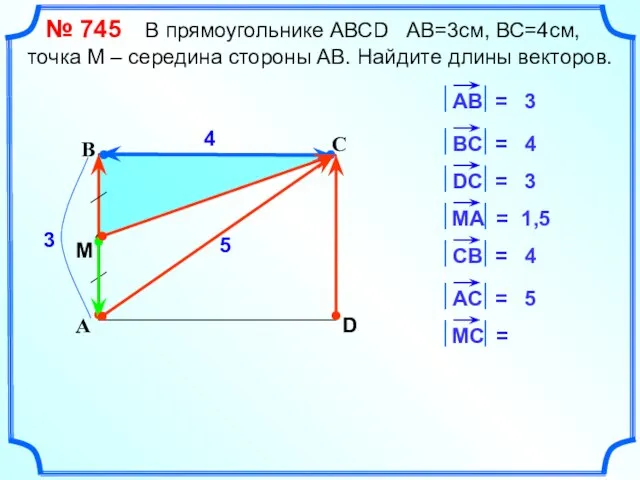
- 13. С А В D 4 3 4 3 1,5 4 5 5 M № 745 В
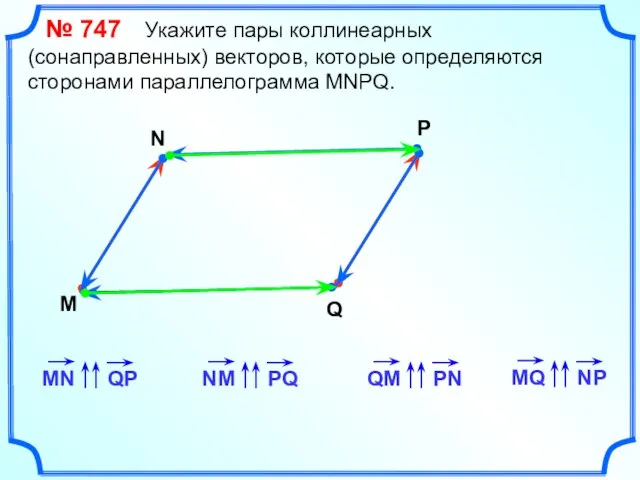
- 14. № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами параллелограмма MNPQ. M N P Q
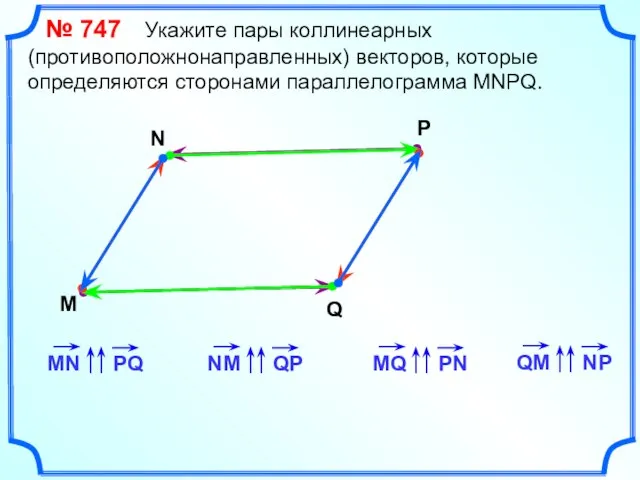
- 15. № 747 Укажите пары коллинеарных (противоположнонаправленных) векторов, которые определяются сторонами параллелограмма MNPQ. M N P Q
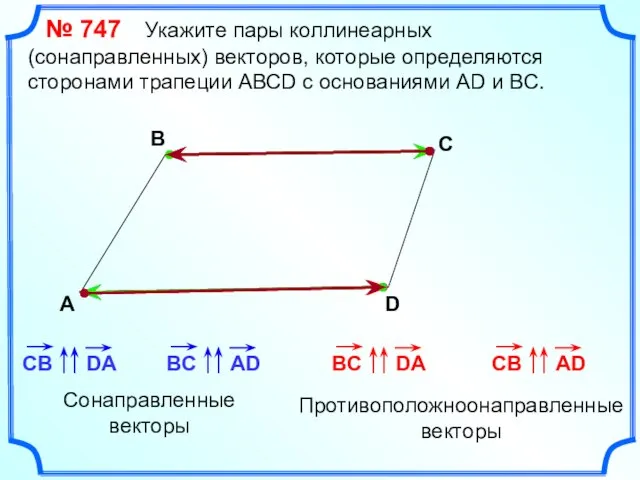
- 16. № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами трапеции АВСD с основаниями AD и
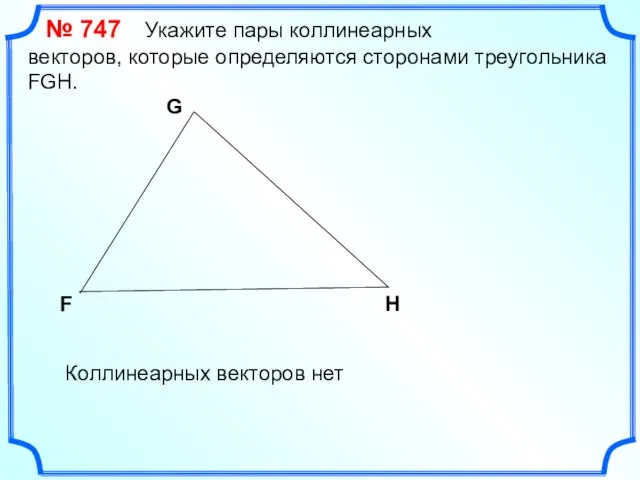
- 17. № 747 Укажите пары коллинеарных векторов, которые определяются сторонами треугольника FGH. F G H Коллинеарных векторов
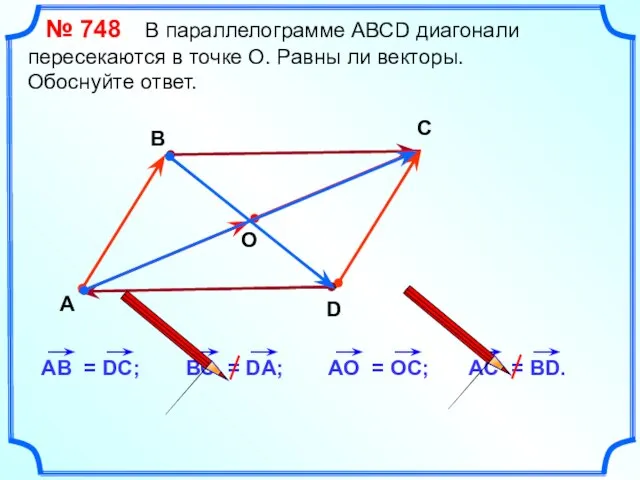
- 18. № 748 В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ. А
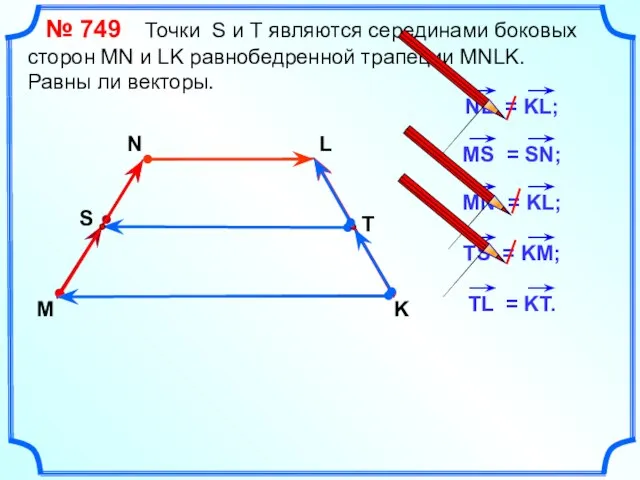
- 19. № 749 Точки S и Т являются серединами боковых сторон MN и LK равнобедренной трапеции MNLK.
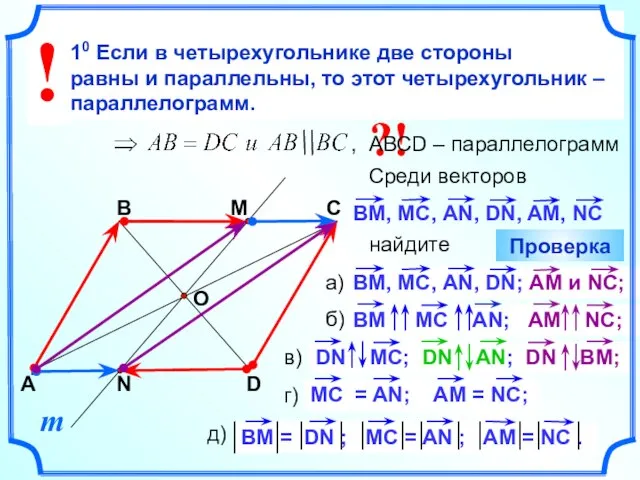
- 20. а) коллинеарные векторы; б) сонаправленные векторы; в) противоположные векторы; г) равные векторы; д) векторы, имеющие равные
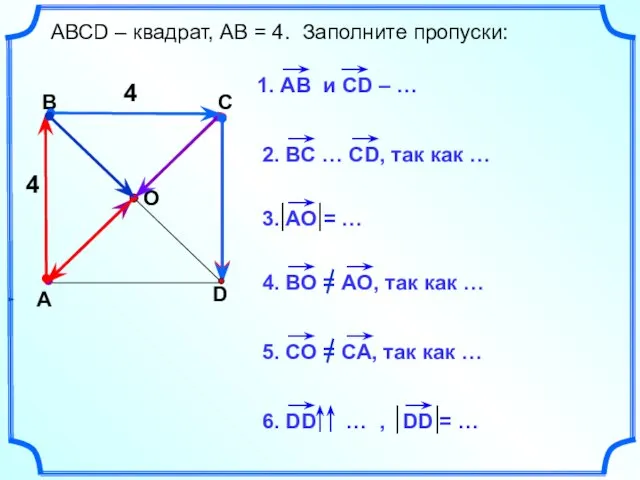
- 21. АВСD – квадрат, АВ = 4. Заполните пропуски: 4 4
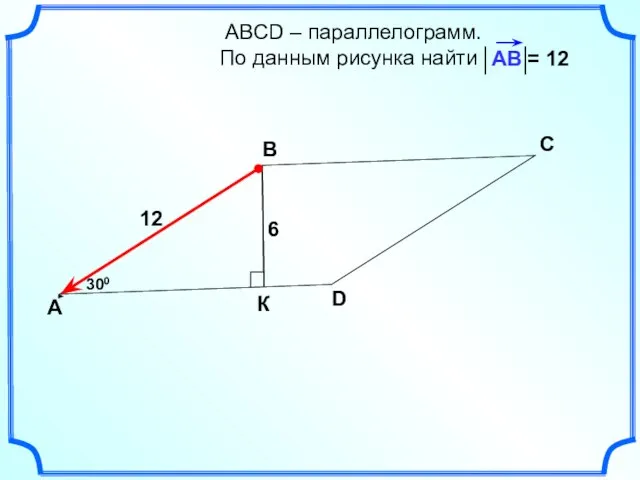
- 22. АВСD – параллелограмм. По данным рисунка найти А В С D 300 6 К 12 =
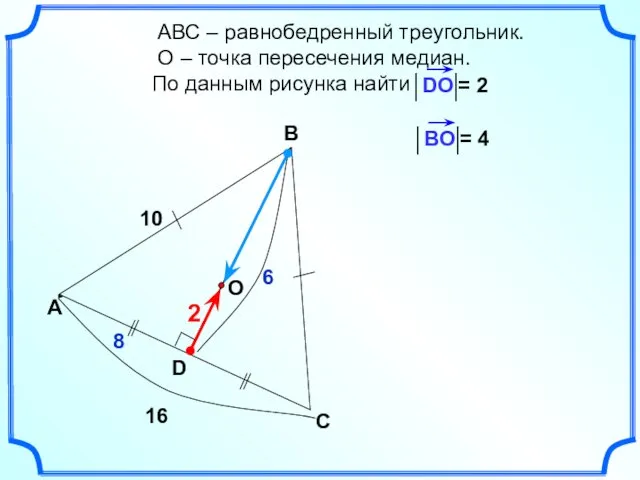
- 23. АВС – равнобедренный треугольник. О – точка пересечения медиан. По данным рисунка найти А В С
- 25. Скачать презентацию
 Лампочки
Лампочки Потребность. Блага. Услуги. Ресурсы
Потребность. Блага. Услуги. Ресурсы Выборы в Государственную Думу 2011 года
Выборы в Государственную Думу 2011 года Савала
Савала Бюджетное правило и валюта
Бюджетное правило и валюта Алексей Архипович Леонов Художник – фантаст
Алексей Архипович Леонов Художник – фантаст Риск среди семей
Риск среди семей ПроектНебезпеки на вулицях і дорогах
ПроектНебезпеки на вулицях і дорогах Хоббит: обратно
Хоббит: обратно Презентация инструментов оценки HOGANдля тренеров и коучей18 декабря 2009
Презентация инструментов оценки HOGANдля тренеров и коучей18 декабря 2009 Перинатальное поражение
Перинатальное поражение Использование представителями бизнеса услуг фирм-однодневок и меры ответственности за их создание через подставных лиц
Использование представителями бизнеса услуг фирм-однодневок и меры ответственности за их создание через подставных лиц Основные процессы проекта
Основные процессы проекта Gap year in Russia
Gap year in Russia Neuropsychology of Memory
Neuropsychology of Memory  Современные средства поражения (продолжение). Занятие №10, часть 2
Современные средства поражения (продолжение). Занятие №10, часть 2 Презентация на тему ДЕНЬ МАТЕРИ
Презентация на тему ДЕНЬ МАТЕРИ  Восстановление кадрового учета
Восстановление кадрового учета Налогообложение юридических лиц
Налогообложение юридических лиц Россия при Петре I
Россия при Петре I Техника жестикуляции
Техника жестикуляции Линейная стилизация
Линейная стилизация Разработка роботизированного комплекса обследования конструкций нефтяных вышек
Разработка роботизированного комплекса обследования конструкций нефтяных вышек Презентация на тему Экосистемы Земли
Презентация на тему Экосистемы Земли Тест по теме «Звук. Отражение звука»
Тест по теме «Звук. Отражение звука» Игра: где логика. Найди общее
Игра: где логика. Найди общее Создание куклы в народном стиле из подсобных материалов
Создание куклы в народном стиле из подсобных материалов Конструирование брюк
Конструирование брюк