Слайд 2Автор:
Шедиков Андрей,
9 класс
МОУ «Солерудниковская
гимназия»

Слайд 3Проблемный вопрос
Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?

Слайд 4Этапы работы:
Обсудили вопрос с учителем.
Нашли информацию.
Исследовали периметры многоугольников, имеющих одинаковую площадь.
Сделали

вывод.
Оформили отчёт.
Слайд 5Пчёлы – удивительные творения природы. Свои геометрические способности они проявляют при построении

сот.
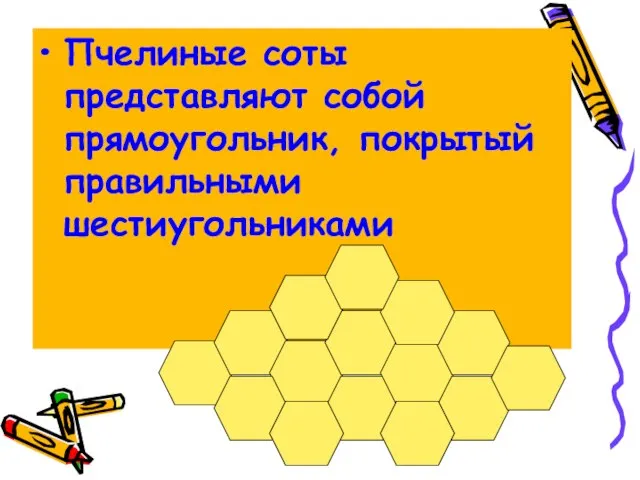
Слайд 6Пчелиные соты представляют собой прямоугольник, покрытый правильными шестиугольниками
Слайд 7Почему пчелы выбрали именно шестиугольник?
Чтобы ответить на этот вопрос, надо сравнить периметры

разных многоугольников, имеющих одинаковую площадь.
Слайд 8 Из всех правильных многоугольников только треугольниками, квадратами и шестиугольниками можно заполнить

плоскость без пробелов и наложений.
Так как в этом случае сумма углов, сходящихся в одной вершине, равна 360˚
(60˚·6=360˚; 90˚·4=360˚; 120˚·3=360˚).
Поэтому пчелы должны «выбрать» одну из этих фигур.
Слайд 9Сравним периметры этих многоугольников, если их площади равны. Имеем:

Слайд 10 Как не согласиться с мнением Пчелы из сказки «Тысяча и одна

ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».
Слайд 11Вывод:
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и

воск для изготовления ячеек.
Слайд 12Источники:
Глухова А., Правильные многоугольники в природе. Математика. Еженедельное учебно-методическое приложение к газете

« Первое сентября», № 38, 1999.
Фирсина С., Правильные многоугольники. Математика. Еженедельное учебно-методическое приложение к газете « Первое сентября», № 10, 2000.
Шарыгин И.Ф.,Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для 5-6 классов. - М.: МИРОС, 1992.











 Семинар Диаграмма Fe-C
Семинар Диаграмма Fe-C На пожаре
На пожаре Презентация на тему Алтайские горы
Презентация на тему Алтайские горы “Зачем” и “почему” в выборе тренинговых программ для корпоративного обучения
“Зачем” и “почему” в выборе тренинговых программ для корпоративного обучения Личностный опросник ТОП-ЮНИТ:Тест как комплексное решение для диагностики менеджерских качеств
Личностный опросник ТОП-ЮНИТ:Тест как комплексное решение для диагностики менеджерских качеств Писатели-юбиляры 2011 года
Писатели-юбиляры 2011 года К вопросу о качестве общего образования:
К вопросу о качестве общего образования: Организация книжных выставок - это наука или искусство!?
Организация книжных выставок - это наука или искусство!? 0805
0805 Подготовка обучающихся с ограниченными возможностями здоровья к демонстрационному экзамену по компетенции Поварское дело
Подготовка обучающихся с ограниченными возможностями здоровья к демонстрационному экзамену по компетенции Поварское дело Таблицы по Теории организации
Таблицы по Теории организации Проблемы и критерии дифференциации уголовно-процессуальной формы _
Проблемы и критерии дифференциации уголовно-процессуальной формы _ Онлайн–консультация адвоката Хромых Ларисы Георгиевны по вопросам кредитных обязательств по невероятно низкой цене
Онлайн–консультация адвоката Хромых Ларисы Георгиевны по вопросам кредитных обязательств по невероятно низкой цене Фірмовий стиль компаній
Фірмовий стиль компаній Верность долгу
Верность долгу Русский язык и культура речи. Виртуальная выставка
Русский язык и культура речи. Виртуальная выставка Предложение по реализации проектов в сфере ЖКХ
Предложение по реализации проектов в сфере ЖКХ Ополнительная платная образовательная услуга по социально-коммуникативному развитию Песочная терапия
Ополнительная платная образовательная услуга по социально-коммуникативному развитию Песочная терапия Презентация на тему Формирование Земли
Презентация на тему Формирование Земли  Церковь, государство и общество. Основные институты церковного права в период формирования централизованного государства.
Церковь, государство и общество. Основные институты церковного права в период формирования централизованного государства.  Проектная деятельность в образовании: история и современность
Проектная деятельность в образовании: история и современность Презентация на тему Ткани животных и растений
Презентация на тему Ткани животных и растений Основные направления деятельности Союза Российских Пивоваровна 2007-2009 гг.
Основные направления деятельности Союза Российских Пивоваровна 2007-2009 гг. Исследование и разработка методов цифровой обработки сигналов в авиации
Исследование и разработка методов цифровой обработки сигналов в авиации  Слагаемые успеха в бизнесе
Слагаемые успеха в бизнесе Поощрения и наказания в воспитании детей
Поощрения и наказания в воспитании детей Способы изменения внутренней энергии тела
Способы изменения внутренней энергии тела Как предотвратить образование угрей
Как предотвратить образование угрей