Содержание
- 2. Обучающая цель: формирование умений и навыков построения сечений. Развивающая цель: формирование и развитие у учащихся пространственного
- 3. Структура урока Организационный момент Целеполагание и мотивация Актуализация знаний Изучение нового материала Закрепление Домашнее задание Рефлексия.
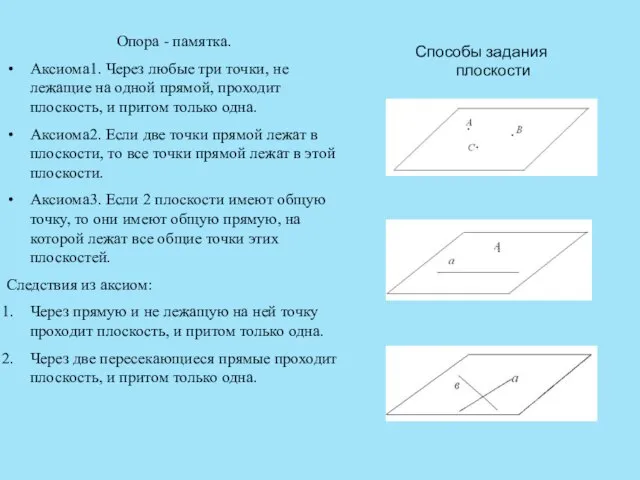
- 4. Опора - памятка. Аксиома1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и
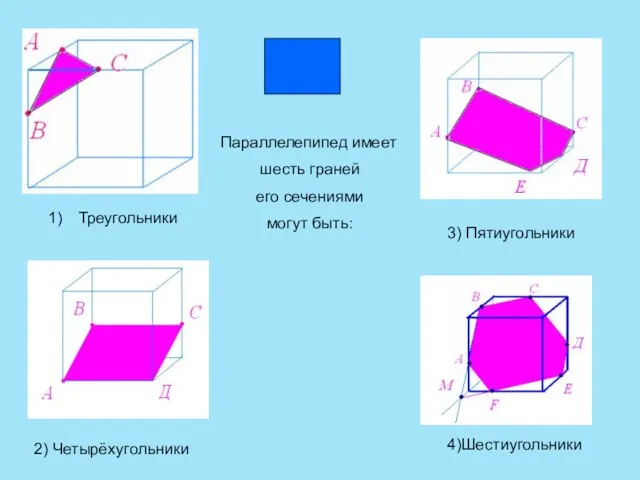
- 6. Параллелепипед имеет шесть граней его сечениями могут быть: Треугольники 2) Четырёхугольники 3) Пятиугольники 4)Шестиугольники
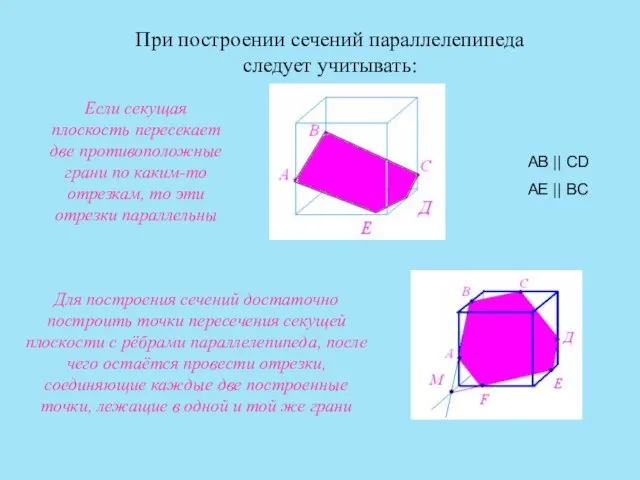
- 7. При построении сечений параллелепипеда следует учитывать: Для построения сечений достаточно построить точки пересечения секущей плоскости с
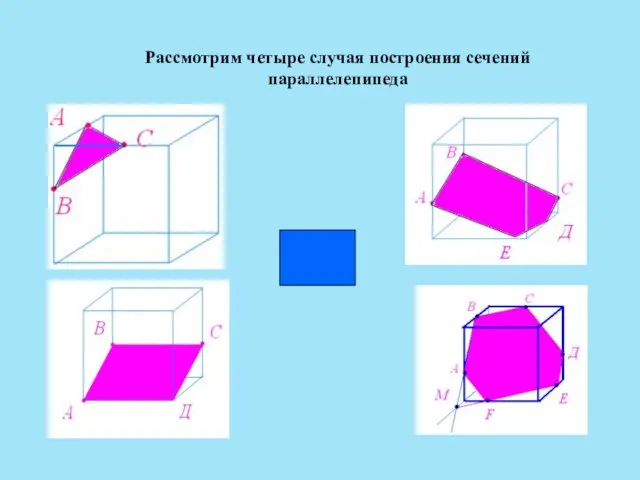
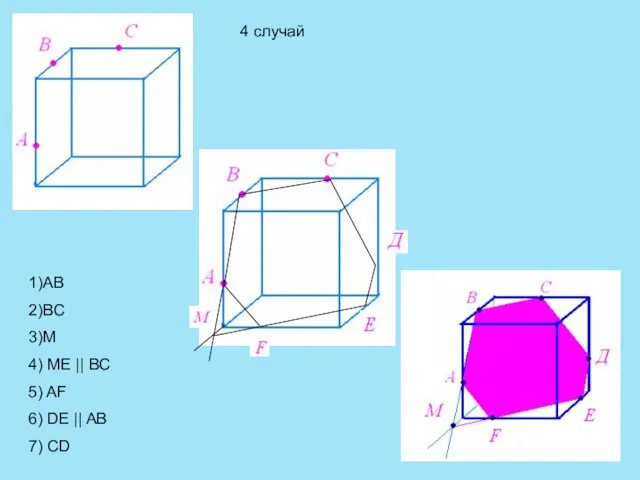
- 8. Рассмотрим четыре случая построения сечений параллелепипеда
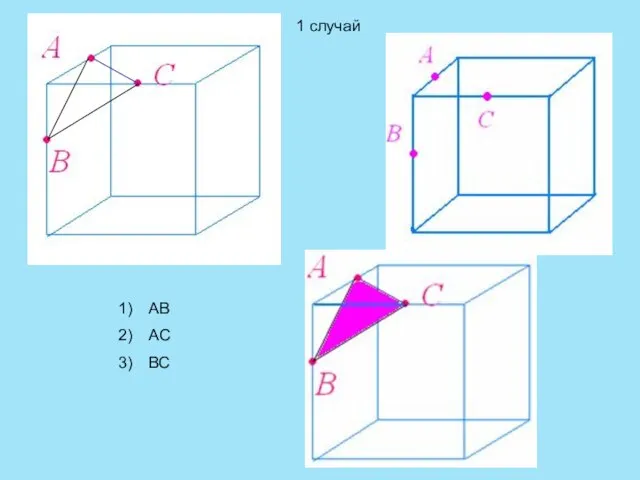
- 9. АВ АС ВС 1 случай
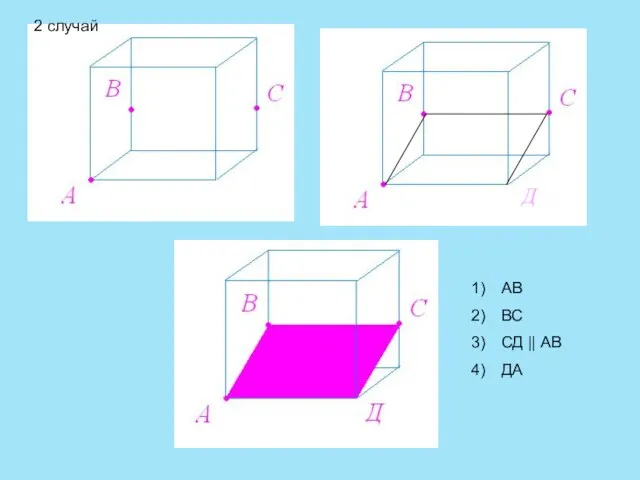
- 10. Д АВ ВС СД || АВ ДА 2 случай
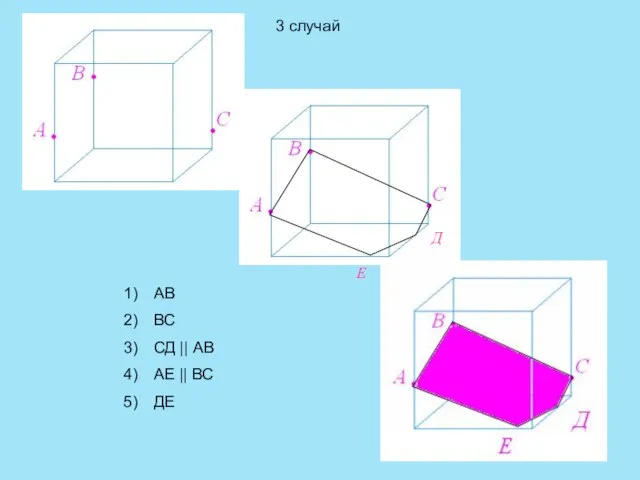
- 11. Д Е АВ ВС СД || АВ АЕ || ВС ДЕ 3 случай
- 12. 1)АВ 2)ВС 3)М 4) МЕ || BC 5) AF 6) DE || AB 7) CD 4
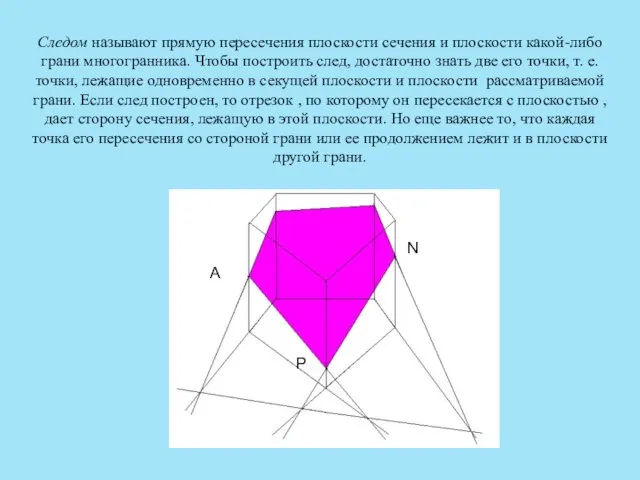
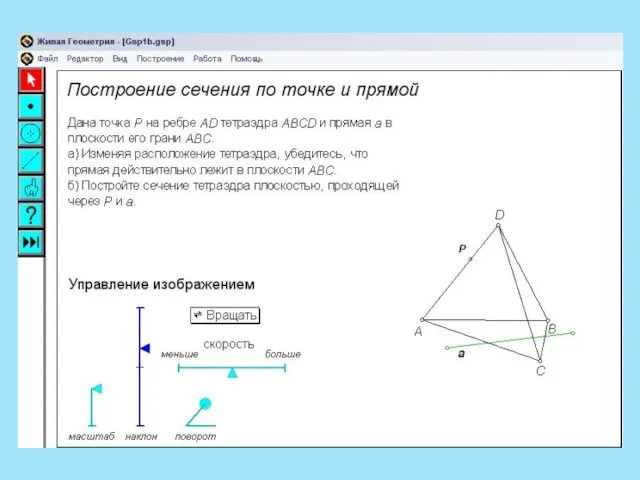
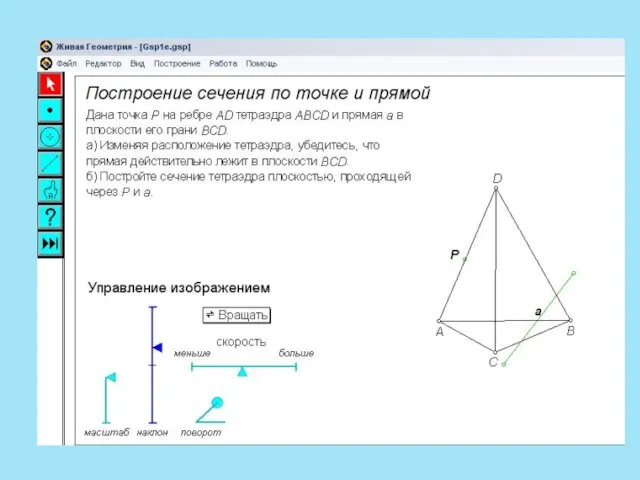
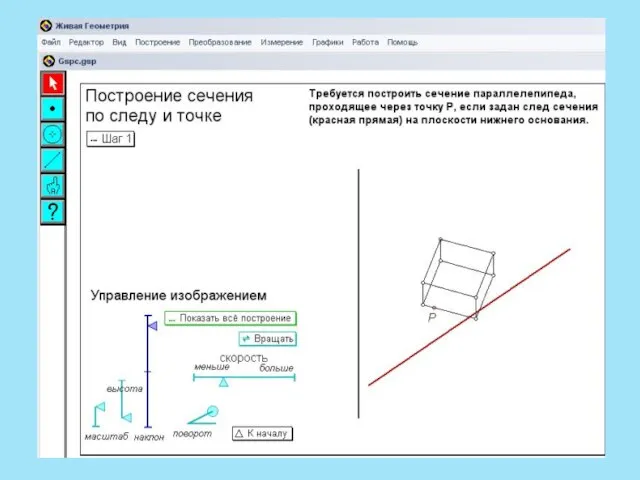
- 13. Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника. Чтобы построить след, достаточно знать
- 14. Метод следов включает три важных пункта: Строим линию пересечения (след) секущей плоскости с плоскостью основания многогранника
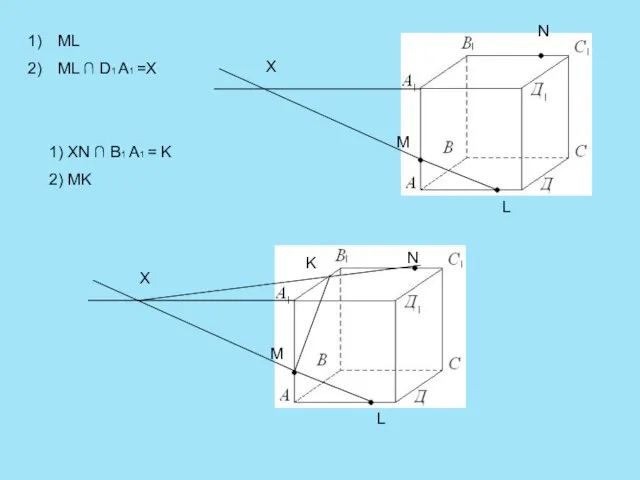
- 15. N L M X N L M X K ML ML ∩ D1 A1 =X 1)
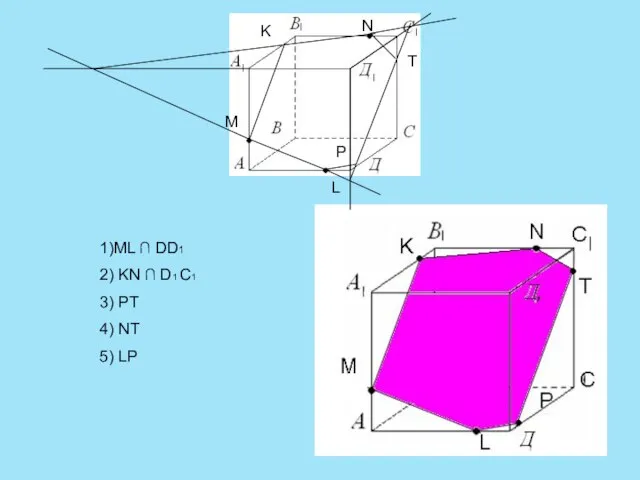
- 16. N L M K Р Т 1)ML ∩ DD1 2) KN ∩ D1 C1 3) PT
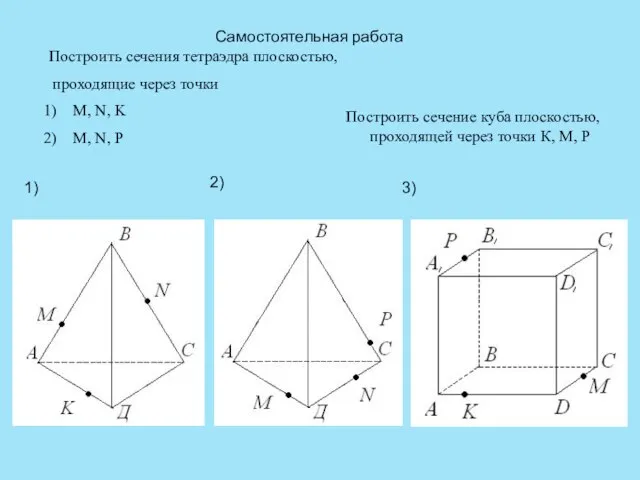
- 17. Самостоятельная работа Построить сечения тетраэдра плоскостью, проходящие через точки M, N, K M, N, P 1)
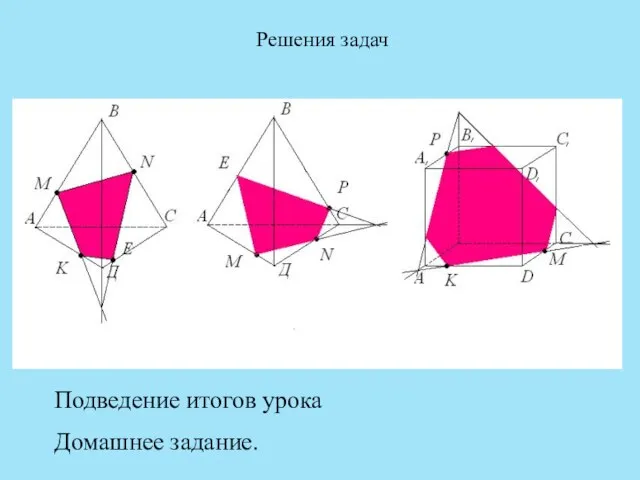
- 18. Решения задач Подведение итогов урока Домашнее задание.
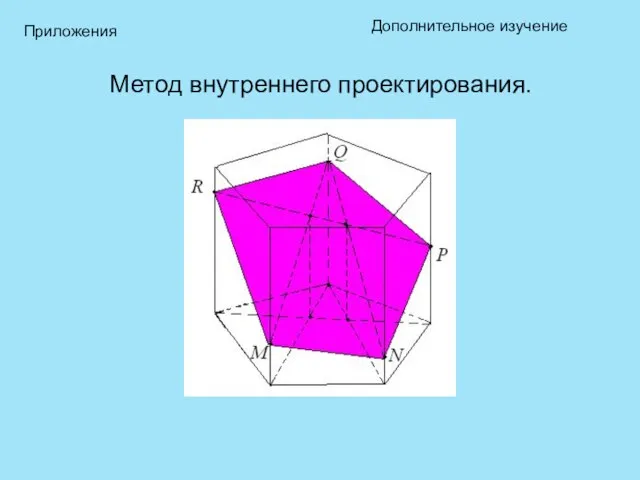
- 19. Метод внутреннего проектирования. Дополнительное изучение Приложения
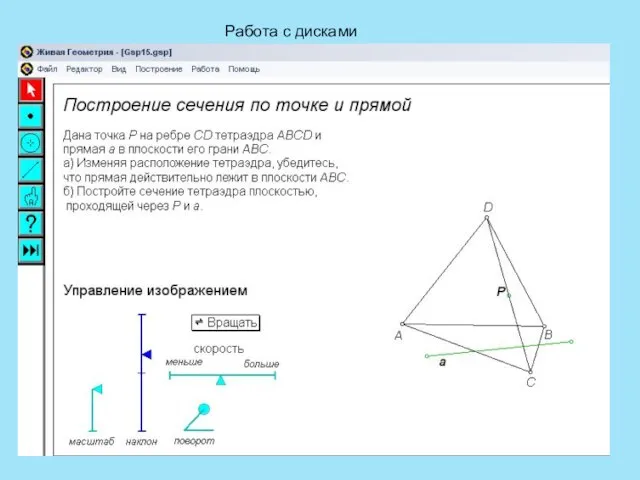
- 20. Работа с дисками
- 25. Скачать презентацию



 Приемы компрессии текста
Приемы компрессии текста  Восприятие при длительном общении. Эмпатия, идентификация, рефлексия, атрибуция, аттракция
Восприятие при длительном общении. Эмпатия, идентификация, рефлексия, атрибуция, аттракция Азбука Красноярья
Азбука Красноярья Управление организациями. Теоретические положения процессного подхода
Управление организациями. Теоретические положения процессного подхода What colour is it?
What colour is it? A new educational future - Новое образовательное будущее
A new educational future - Новое образовательное будущее Мотивация как функция менеджмента
Мотивация как функция менеджмента Мои компетенции в сфере управления
Мои компетенции в сфере управления Суша планеты
Суша планеты Научно-методические принципы организации подготовки преподавателей естественнонаучных дисциплин к профессиональной деятельн
Научно-методические принципы организации подготовки преподавателей естественнонаучных дисциплин к профессиональной деятельн Костюм Чеховской эпохи
Костюм Чеховской эпохи Практические методы и руководство по вычислению параметров трещиностойкости конструкций с применением систем MSC.Software
Практические методы и руководство по вычислению параметров трещиностойкости конструкций с применением систем MSC.Software OpenOffice
OpenOffice Слово и время
Слово и время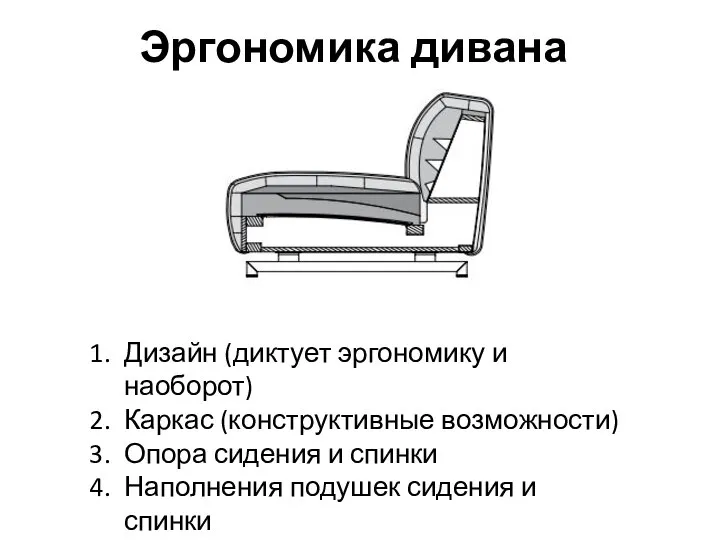 Эргономика дивана
Эргономика дивана Презентация на тему Площадь прямоугольника
Презентация на тему Площадь прямоугольника Заикание.
Заикание. Лекции 6 - 7
Лекции 6 - 7 Презентация на тему Новое время:Встреча Европы и Америки Программа А.Плешакова Окружающий мир 4 класс
Презентация на тему Новое время:Встреча Европы и Америки Программа А.Плешакова Окружающий мир 4 класс  Свето-теневой рисунок. Курс Кинооператорство
Свето-теневой рисунок. Курс Кинооператорство ПРЕДМЕТЫ ДОМАШНЕГО ОБИХОДА
ПРЕДМЕТЫ ДОМАШНЕГО ОБИХОДА Изучаем среднее арифметическое
Изучаем среднее арифметическое Автомобили - старинные и современные
Автомобили - старинные и современные Репродукции картин русских художников
Репродукции картин русских художников Фланцевое соединение
Фланцевое соединение Приглашаем на работу
Приглашаем на работу Методики применения средств физической культуры для направленной коррекции телосложения
Методики применения средств физической культуры для направленной коррекции телосложения Jak uczyć wyłącznie po polsku
Jak uczyć wyłącznie po polsku