Содержание
Слайд 31.Построение треугольника по трем сторонам.
-Анализ: при помощи линейки можно провести луч АВ,
1.Построение треугольника по трем сторонам.
-Анализ: при помощи линейки можно провести луч АВ,

при помощи циркуля – построить на нем отрезок заданной длины.
Вершина С находится на пересечении множеств точек, удаленных на расстояние АС от точки А (окружности с центром в точке А и радиусом АС), и множества точек, удаленных на расстояние ВС от точки В ( окружность с центром в точке В радиусом ВС).
-Построение циркулем и линейкой:
1.Строим ,
2.Откладываем на нем .
3.Строим окружность с центром в точке А радиусом АС.
4.Строим окружность с центром в точке В радиусом ВС.
5. Точка пересечения окружностей является третьей вершиной треугольника.
Вершина С находится на пересечении множеств точек, удаленных на расстояние АС от точки А (окружности с центром в точке А и радиусом АС), и множества точек, удаленных на расстояние ВС от точки В ( окружность с центром в точке В радиусом ВС).
-Построение циркулем и линейкой:
1.Строим ,
2.Откладываем на нем .
3.Строим окружность с центром в точке А радиусом АС.
4.Строим окружность с центром в точке В радиусом ВС.
5. Точка пересечения окружностей является третьей вершиной треугольника.
Слайд 52.Построение угла, равного данному.
-Анализ: сводим задачу к построению равного треугольника циркулем
2.Построение угла, равного данному.
-Анализ: сводим задачу к построению равного треугольника циркулем

и линейкой и к повороту в построении в «Живой геометрии».
-Построение циркулем и линейкой:
Проводим окружность с центром в вершине заданного угла, точки пересечения окружности со сторонами угла и вершина угла образуют треугольник, одним из углов которого является заданный угол.
-Построение циркулем и линейкой:
Проводим окружность с центром в вершине заданного угла, точки пересечения окружности со сторонами угла и вершина угла образуют треугольник, одним из углов которого является заданный угол.


 НазванияХимическихЭлементов
НазванияХимическихЭлементов Акты применения права. Характеристика и классификация
Акты применения права. Характеристика и классификация САМЫЕ-САМЫЕ
САМЫЕ-САМЫЕ Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Невидимые нити (2 класс)
Невидимые нити (2 класс) НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ
НИКОЛАЯ ДМИТРИЕВИЧА ПАПАЛЕКСИ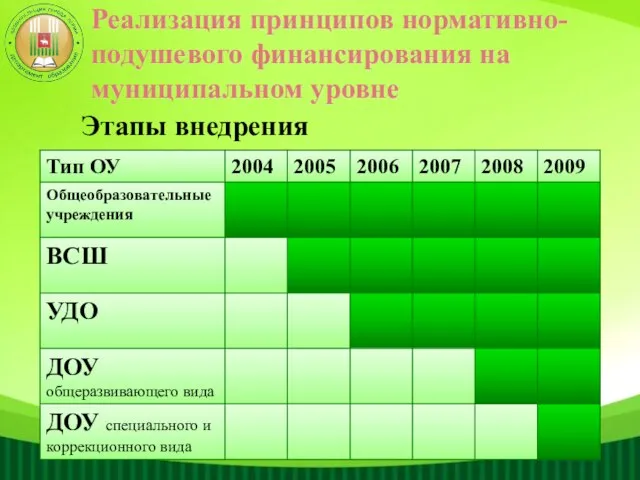 Реализация принципов нормативно-подушевого финансирования на муниципальном уровне
Реализация принципов нормативно-подушевого финансирования на муниципальном уровне Верейская по деньгам - ИТОГ
Верейская по деньгам - ИТОГ Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер
Дизайнер в отечественном ИТ бизнесе: многообразие деятельности, недооцененные компоненты профессионализма, стратегия роста Сер Симметрия в архитектуре
Симметрия в архитектуре Презентация на тему Основные типы задач на проценты
Презентация на тему Основные типы задач на проценты  Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ
Вопросы внедрения национальной Интернет-адресации (IDN) .КАЗ Шаблон. Название темы
Шаблон. Название темы Презентация на тему Деревья
Презентация на тему Деревья  Учимся рисовать синичку (1)
Учимся рисовать синичку (1) Ох, уж эта функция
Ох, уж эта функция ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ
ЕДИНАЯ СИСТЕМА КЛАССИФИКАТОРОВ АНАЛИТИЧЕСКИХ ДАННЫХ Основы программирования промышленных роботов
Основы программирования промышленных роботов Образ матери в искусстве
Образ матери в искусстве Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы
Исследование опорно-двигательного аппарата учащихся Кугультинской средней школы Шар ( сфера )
Шар ( сфера ) Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2
Школа нумерологии Светланы Сорокиной. Основы нумерологии. Базовый курс. Урок 2 С Новым годом поздравляю
С Новым годом поздравляю Презентация на тему Книжная миниатюра Востока
Презентация на тему Книжная миниатюра Востока  О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ»
О ДОЛГОСРОЧНОМ РЕГУЛИРОВАНИИ ТАРИФОВ НА УСЛУГИ ПО ПЕРЕДАЧЕ ТЕПЛОВОЙ ЭНЕРГИИ ООО «СВЕРДЛОВСКАЯ ТЕПЛОСНАБЖАЮЩАЯ КОМПАНИЯ» Начало Второй Мировой Войны
Начало Второй Мировой Войны Понятие психологии
Понятие психологии Страховые фонды Понятие, сущность, основные формы
Страховые фонды Понятие, сущность, основные формы