Содержание
- 2. Простая поверхность - поверхность, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям (растяжениям, сжатиям и
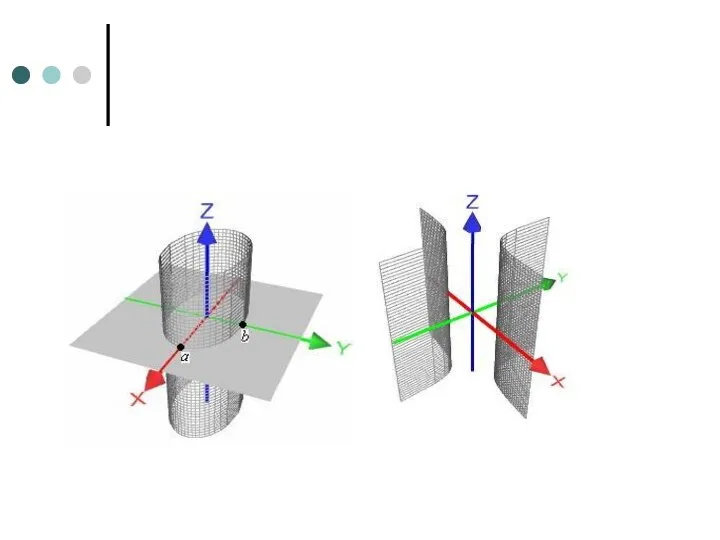
- 4. Лента Мёбиуса Ориентация Важной характеристикой поверхности является её ориентация. Поверхность называется двусторонней, если на всей её
- 5. Бутылка Клейна
- 6. Пример двусторонних поверхностей
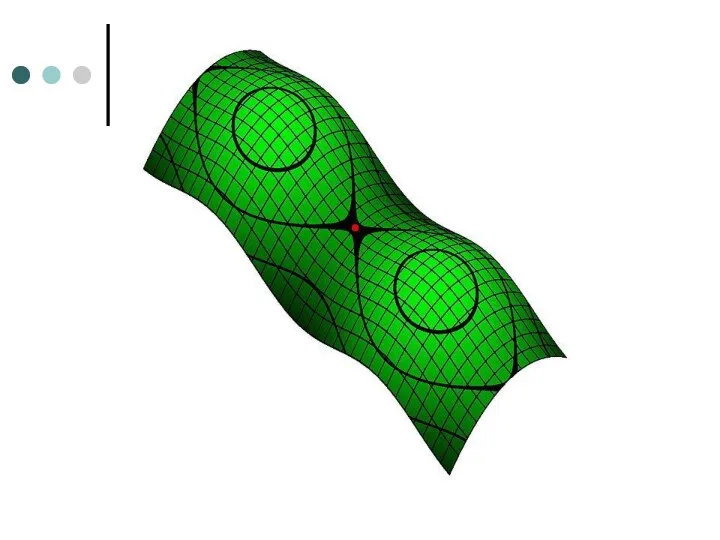
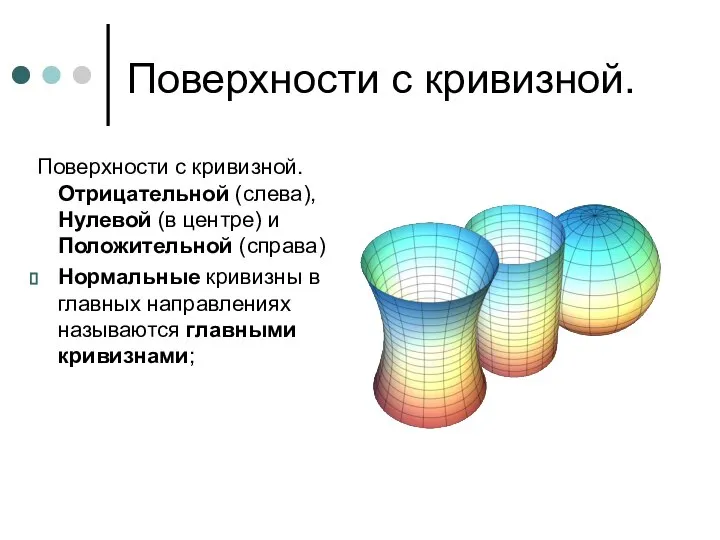
- 7. Поверхности с кривизной. Поверхности с кривизной. Отрицательной (слева), Нулевой (в центре) и Положительной (справа) Нормальные кривизны
- 8. Аналитическое выражение Пусть на плоскости с прямоугольной системой координат u и v задан квадрат, координаты внутренних
- 9. ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ В начертательной геометрии фигуры задаются графически, поэтому целесообразно рассматривать поверхность как совокупность всех
- 10. Определения поверхности Поверхностью называется: совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве. непрерывное двупараметрическое множество
- 11. Задание поверхности Для получения наглядного изображения поверхностиДля получения наглядного изображения поверхности на чертеже закон перемещения линии
- 12. В процессе образования поверхностей линия может оставаться неизменной или менять свою форму. Такой способ образования поверхности
- 13. Поверхности
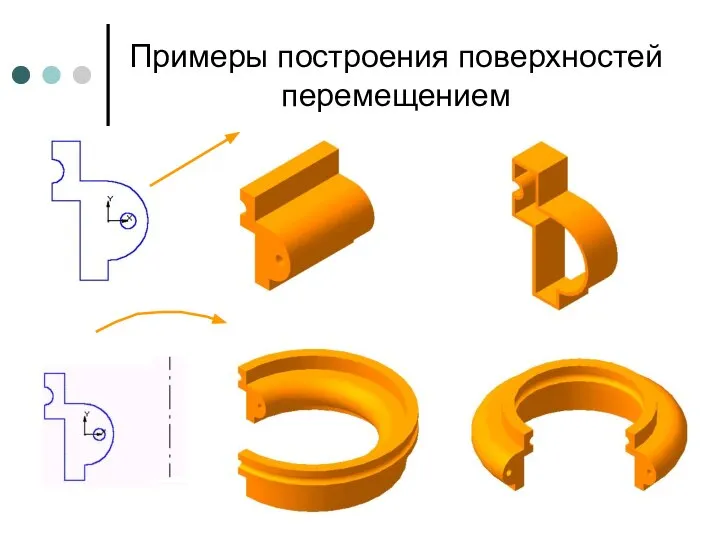
- 14. Примеры построения поверхностей перемещением
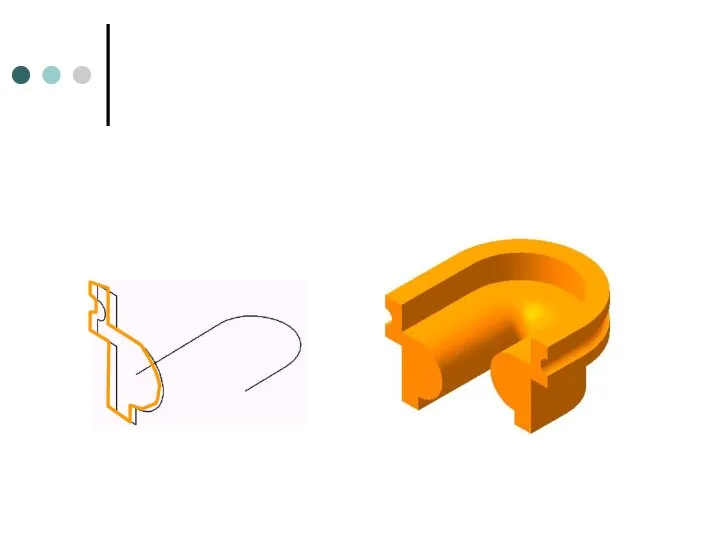
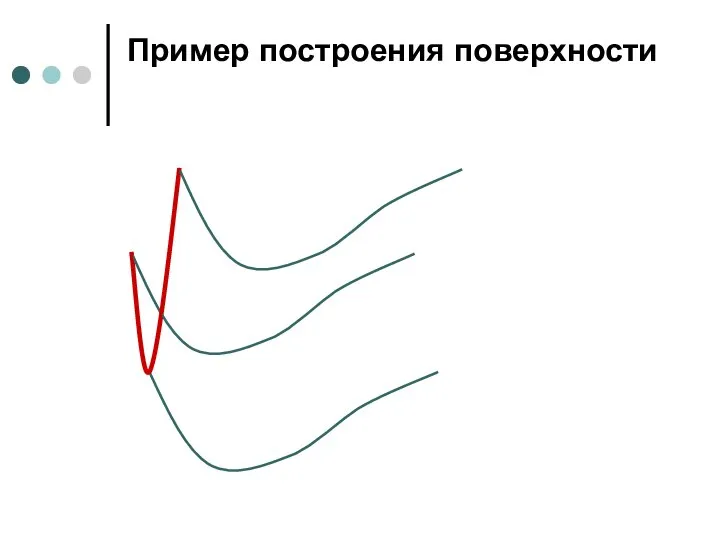
- 16. Пример построения поверхности
- 17. Пример построения поверхности
- 18. Задание кинематической кривой поверхности На чертеже кинематическая кривая поверхность задается при помощи ее определителя. Определителем поверхности
- 19. i
- 20. Примеры образования поверхностей Примером такого способа образования могут служить все технологические процессы обработки металлов режущей кромкой,
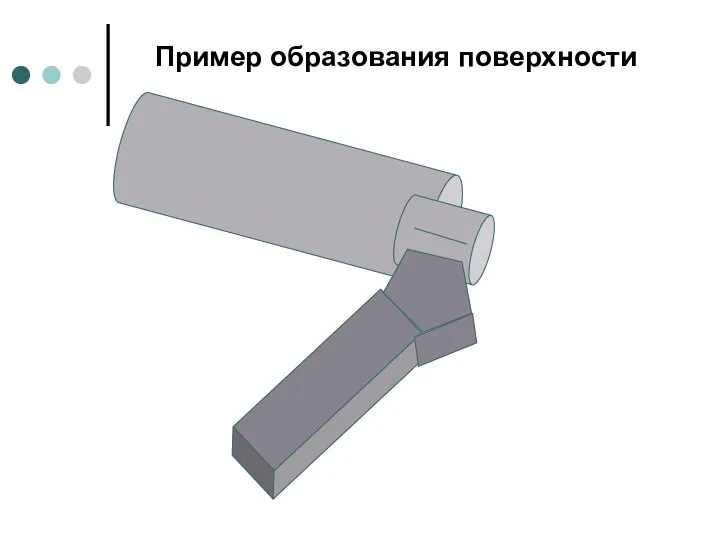
- 22. Пример образования поверхности
- 24. Способы задания кривых поверхностей Кривые поверхности широко применяются в различных областях науки и техники при создании
- 25. Аналитический способ задания поверхности Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает кривую поверхность как множество
- 28. Каркас поверхности Каркасом поверхности принято называть упорядоченное множество точек или линий, принадлежащих поверхности. В зависимости от
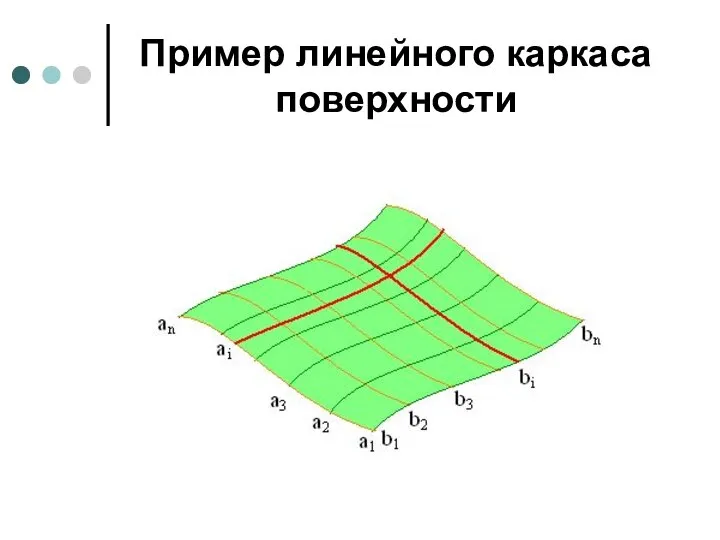
- 29. Эта зависимость характеризуется некоторой изменяющейся величиной, которая называется параметром каркаса. Если параметр линейного каркаса является непрерывной
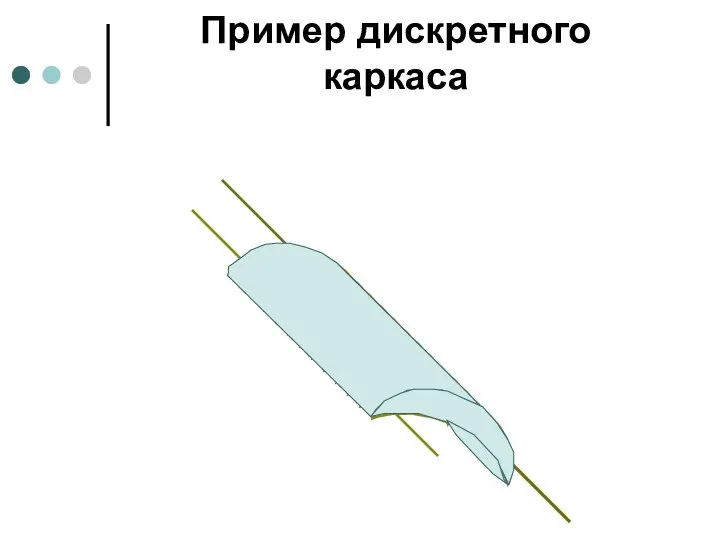
- 30. Пример дискретного каркаса
- 31. Пример линейного каркаса поверхности
- 32. Каркас Упорядоченное множество точек или линий, принадлежащих поверхности, называется каркасом. В зависимости от того, чем задаётся
- 33. Определитель поверхности Кинематический способ образования поверхности можно представить как множество положений движущейся линии или поверхности. Этот
- 34. Состав определителя 1. Геометрическая часть - совокупность геометрических фигур, с помощью которых можно образовать поверхность. 2.
- 35. Выбор определителя поверхности Определитель поверхности выявляется путем анализа способов образования поверхности или ее основных свойств. В
- 36. Определитель поверхности Совокупность параметров, однозначно определяющих данную поверхность, называют определителем. Алгоритмическая часть определителя задаёт закон движения
- 37. Поверхность на комплексном чертеже Поверхность считается заданной на комплексном чертеже, если относительно любой точки пространства, заданной
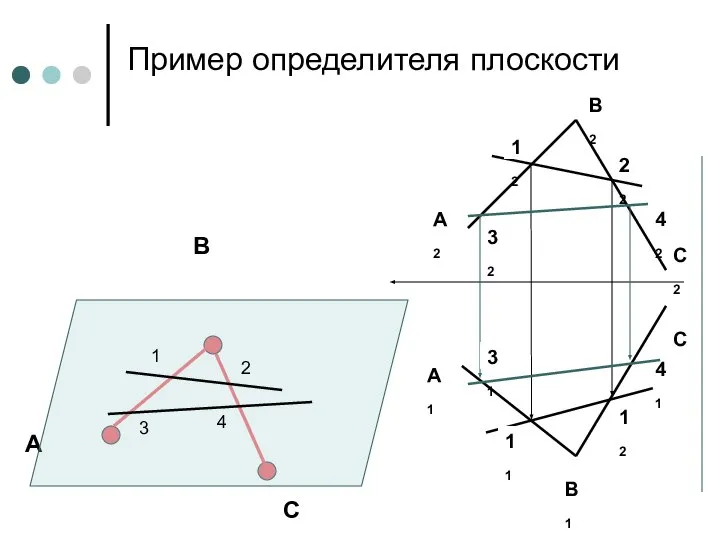
- 38. Примеры определителя поверхностей Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну
- 39. Пример определителя плоскости А2 А1 В1 В2 С2 С1 А В С 1 2 3 4
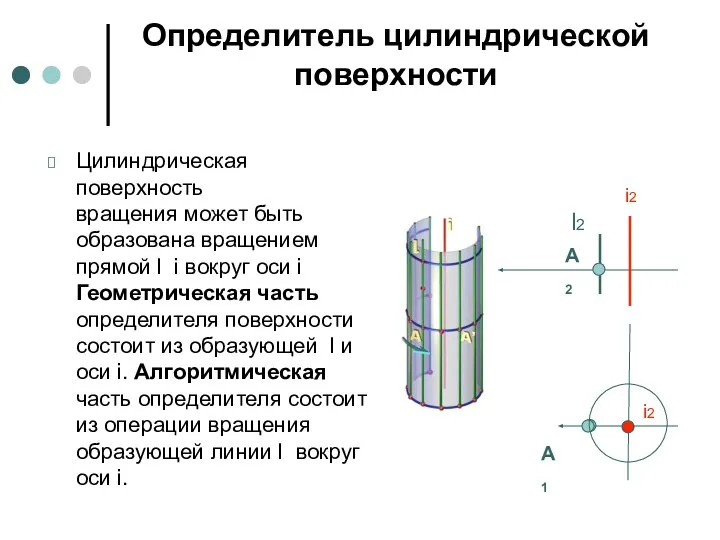
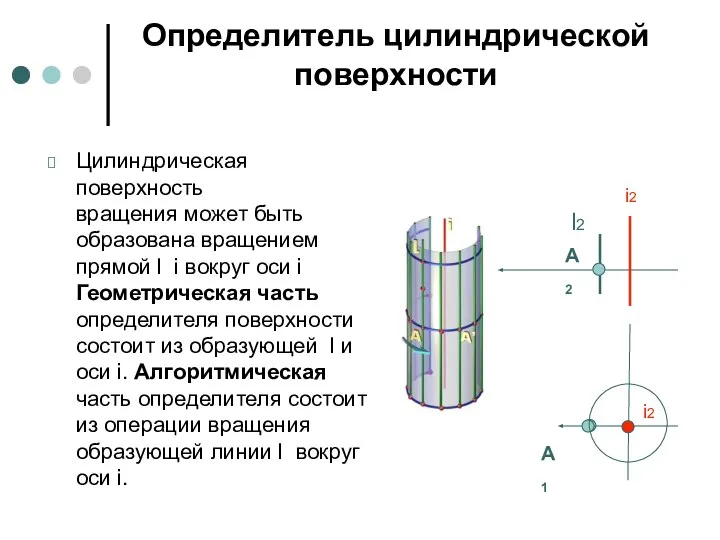
- 40. Определитель цилиндрической поверхности Цилиндрическая поверхность вращения может быть образована вращением прямой l i вокруг оси i
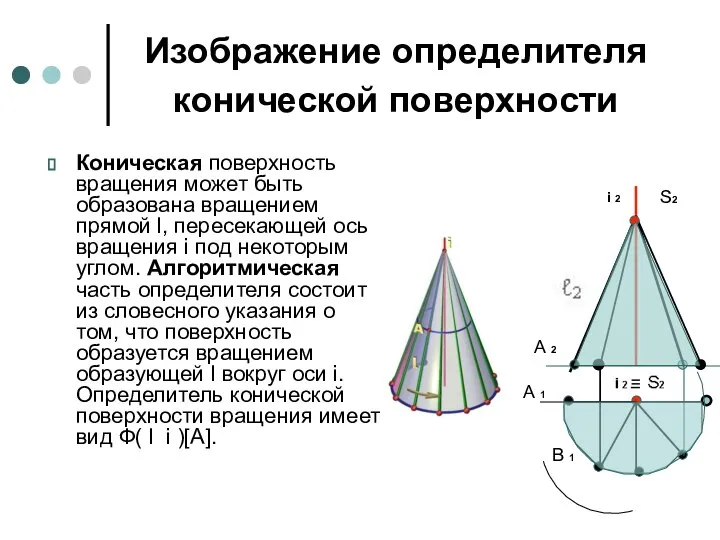
- 41. Изображение определителя конической поверхности Коническая поверхность вращения может быть образована вращением прямой l, пересекающей ось вращения
- 42. Определитель цилиндрической поверхности Цилиндрическая поверхность вращения может быть образована вращением прямой l i вокруг оси i
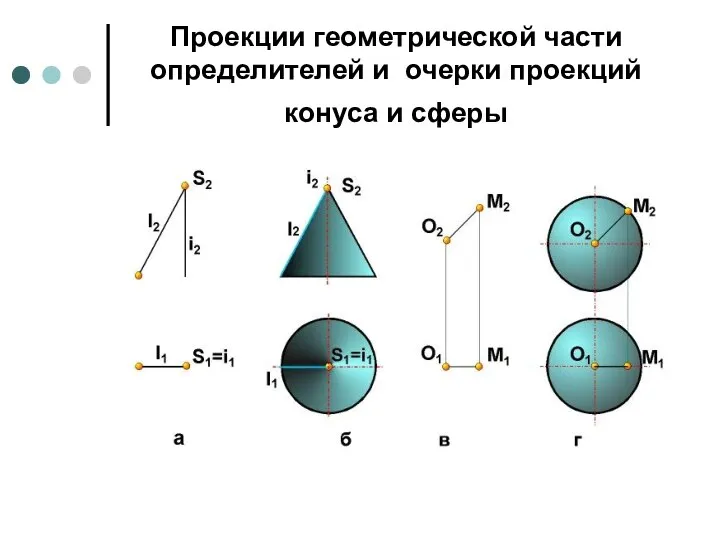
- 43. Проекции геометрической части определителей и очерки проекций конуса и сферы
- 44. Поверхности на комплексном чертеже могут быть заданы: Проекциями направляющих и способом перемещения по ним образующих. Семейством
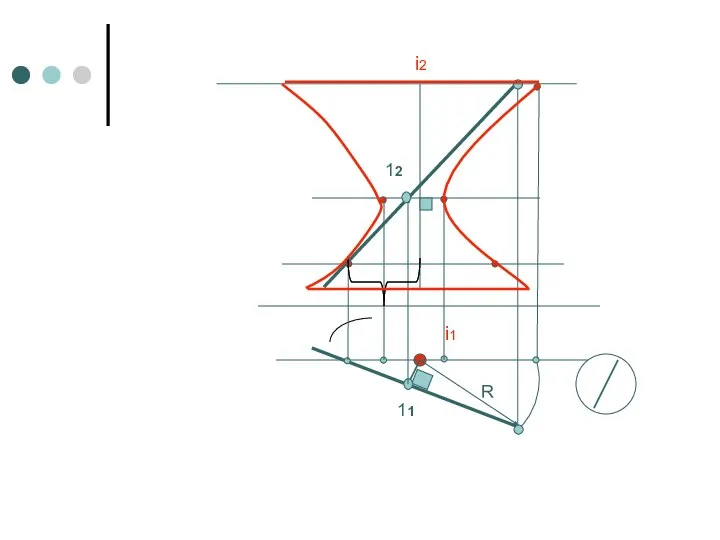
- 45. i2 i1 11 12 R
- 46. Виды кривых поверхностей Кривые поверхности разделяются на линейчатые и нелинейчатые, закономерные и незакономерные. Поверхность называется линейчатой,
- 47. Закономерные поверхности Закономерные поверхности, в зависимости от вида уравнения, разделяются на алгебраические и трансцендентные. Алгебраическое уравнение
- 48. Примеры кривых поверхностей Примерами кривых поверхностей второго порядка могут служить поверхности, образованные вращением кривых второго порядка
- 49. Поверхности
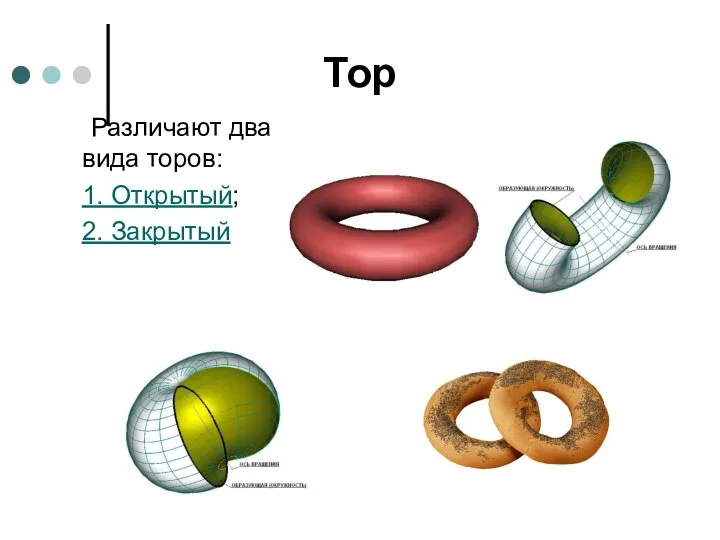
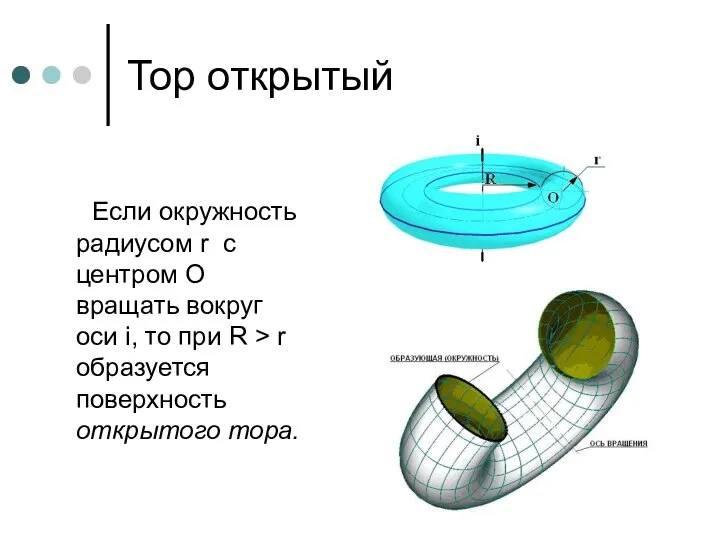
- 50. Тор Различают два вида торов: 1. Открытый; 2. Закрытый
- 51. Тор открытый Если окружность радиусом r с центром О вращать вокруг оси i, то при R
- 52. Тор закрытый Если R
- 53. Кинематические кривые поверхности Наибольшее применение в технике получили кинематические кривые поверхности с образующими постоянной формы: 1.
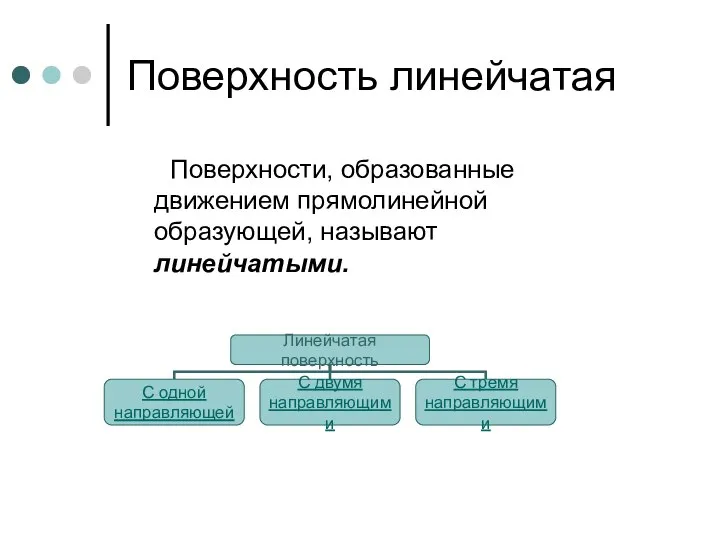
- 54. Поверхность линейчатая Поверхности, образованные движением прямолинейной образующей, называют линейчатыми.
- 55. Поверхность линейчатая с одной направляющей Примерами линейчатых поверхностей с одной направляющей могут быть: - цилиндрическая поверхность;
- 56. Поверхность линейчатая с двумя направляющими Примерами линейчатых поверхностей с двумя направляющими могут быть: - поверхность цилиндроида;
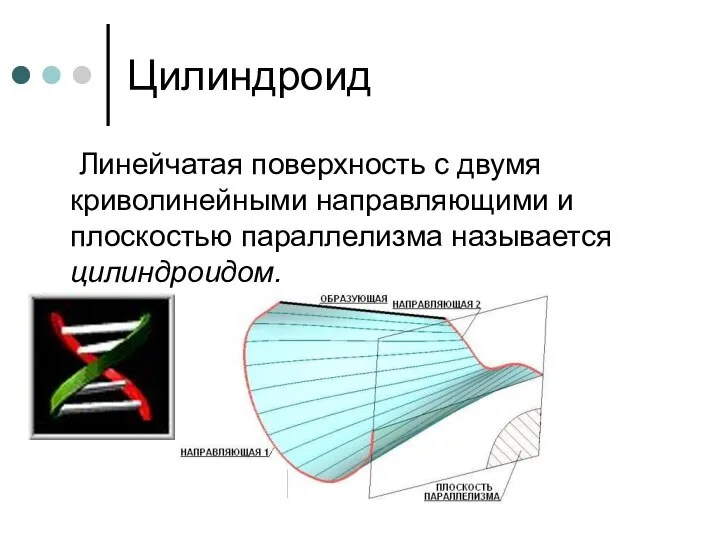
- 57. Цилиндроид Линейчатая поверхность с двумя криволинейными направляющими и плоскостью параллелизма называется цилиндроидом.
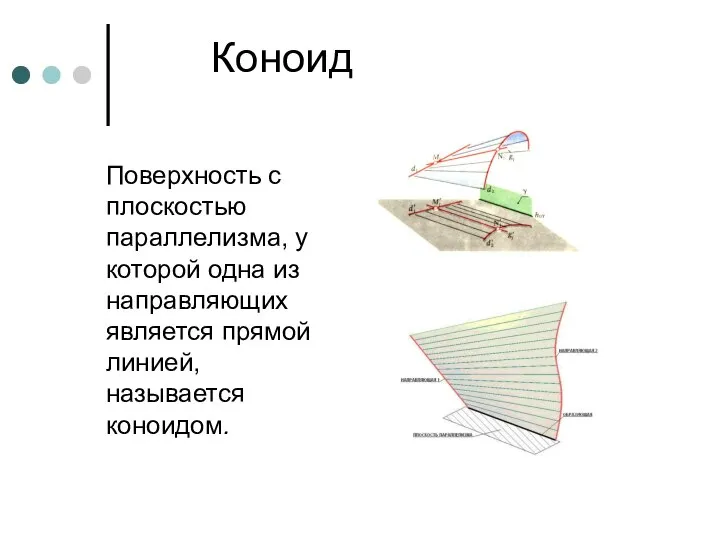
- 58. Коноид Поверхность с плоскостью параллелизма, у которой одна из направляющих является прямой линией, называется коноидом.
- 59. Параболоид гиперболический Поверхность с плоскостью параллелизма и двумя скрещивающимися прямолинейными направляющими называется гиперболическим параболоидом или косой
- 60. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ Как уже отмечалось, поверхность называется линейчатой, если она может быть образована перемещением прямой линии.
- 61. Виды линейчатых поверхностей Линейчатые поверхности разделяются на два вида: 1) развертывающиеся поверхности; 2) неразвертывающиеся, или косые
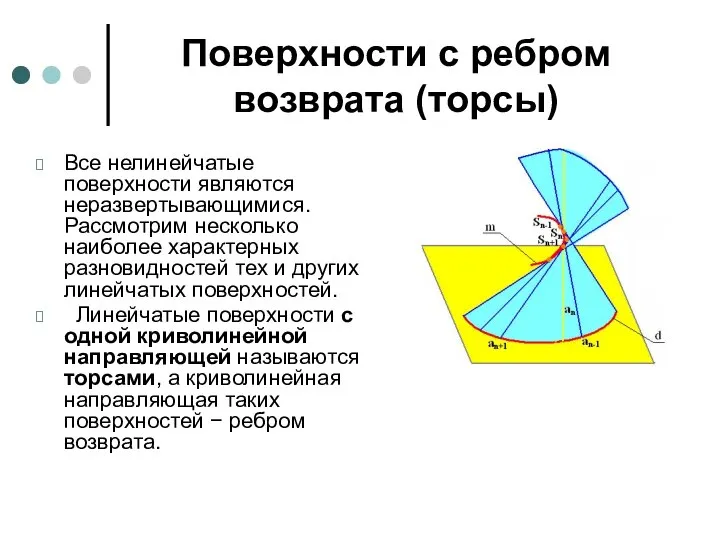
- 62. Поверхности с ребром возврата (торсы) Все нелинейчатые поверхности являются неразвертывающимися. Рассмотрим несколько наиболее характерных разновидностей тех
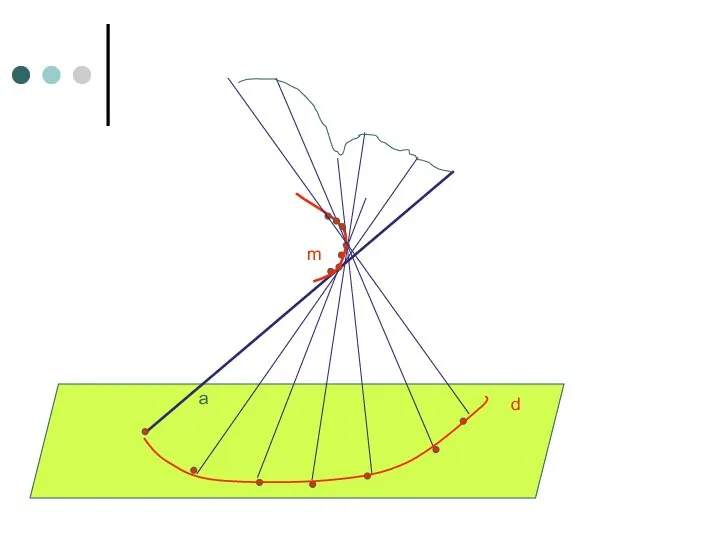
- 63. d m a
- 64. Поверхности развертывающиеся Поверхностью с ребром возврата (торсом) называют поверхность, описываемую движением прямой − образующей, касающейся некоторой
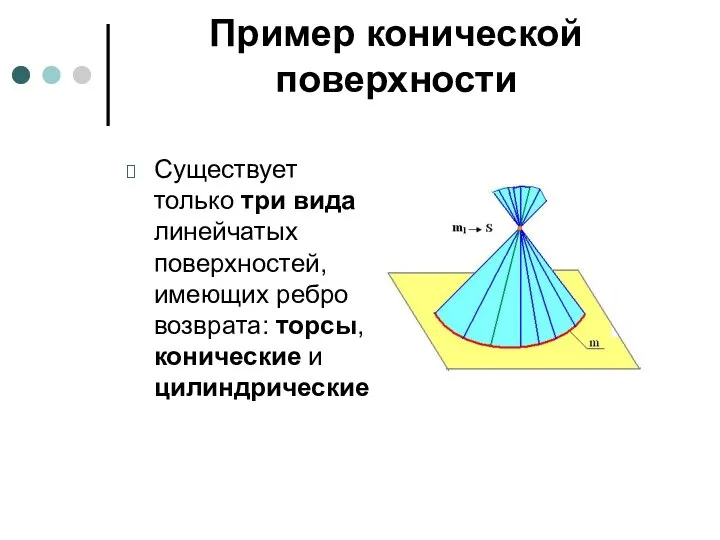
- 65. Пример конической поверхности Существует только три вида линейчатых поверхностей, имеющих ребро возврата: торсы, конические и цилиндрические
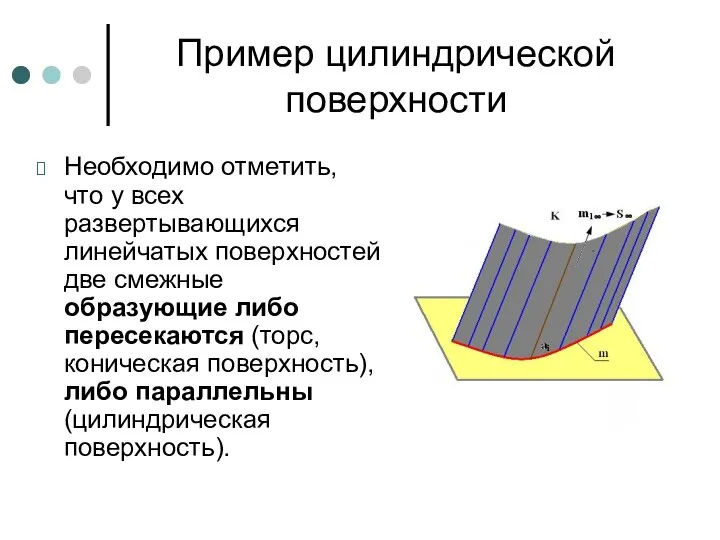
- 66. Пример цилиндрической поверхности Необходимо отметить, что у всех развертывающихся линейчатых поверхностей две смежные образующие либо пересекаются
- 67. НЕРАЗВЕРТЫВАЮЩИЕСЯ (КОСЫЕ) ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ. Неразвертывающиеся линейчатые поверхности в общем случае образуются движением прямолинейной образующей по трем
- 68. Косые поверхности Разновидностями косых поверхностей являются линейчатые поверхности с направляющей плоскостью и частные их виды −
- 69. Поверхность Каталана Поверхности с двумя направляющими и плоскостью параллелизма называют поверхностями Каталана ( по имени бельгийского
- 70. Поверхность линейчатая с тремя направляющими Примерами линейчатых поверхностей с тремя направляющими могут быть: - косой цилиндр;
- 71. Цилиндр косой Линейчатая поверхность с тремя криволинейными направляющими называется поверхностью общего вида, или косым цилиндром.
- 72. Поверхность общего вида Линейчатая поверхность с тремя криволинейными направляющими называется поверхностью общего вида.
- 73. Цилиндроид дважды косой Если одна из направляющих -прямая, поверхность называют дважды косым цилиндроидом.
- 74. Коноид дважды косой Если две направляющие прямые и одна кривая, то поверхность называют дважды косым коноидом.
- 75. Поверхность вращения Поверхность вращения образована вращением образующей вокруг неподвижной прямой — оси. Образующая - может быть
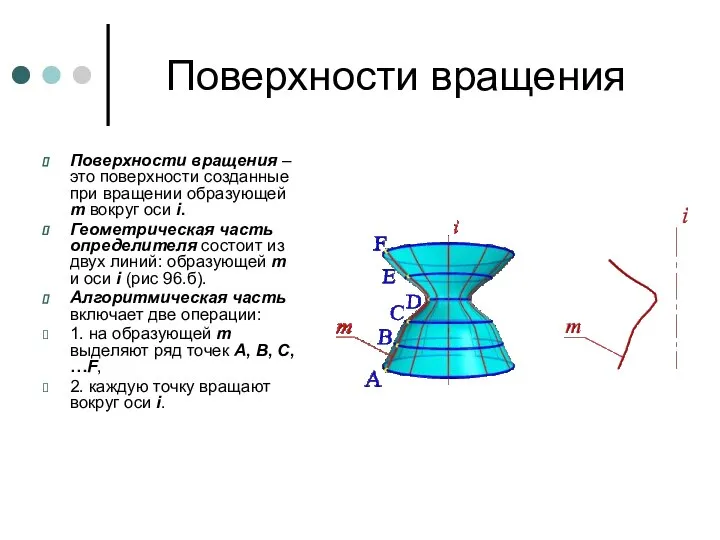
- 76. Поверхности вращения Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i. Геометрическая
- 77. Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i. Эти окружности
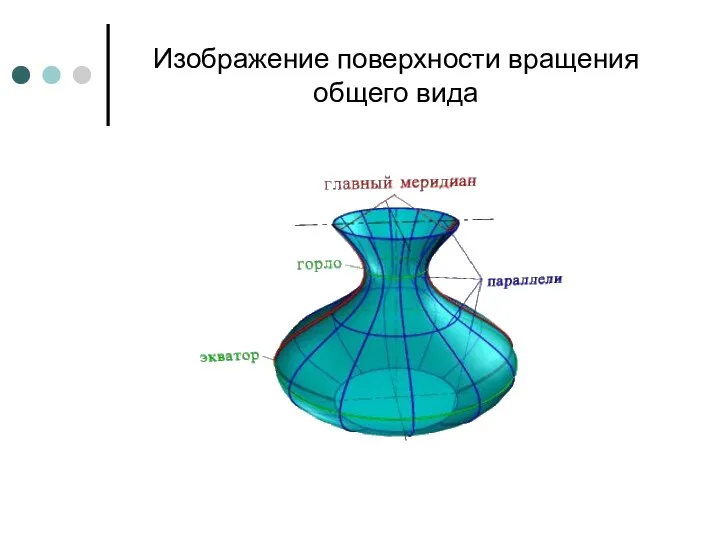
- 78. Изображение поверхности вращения общего вида
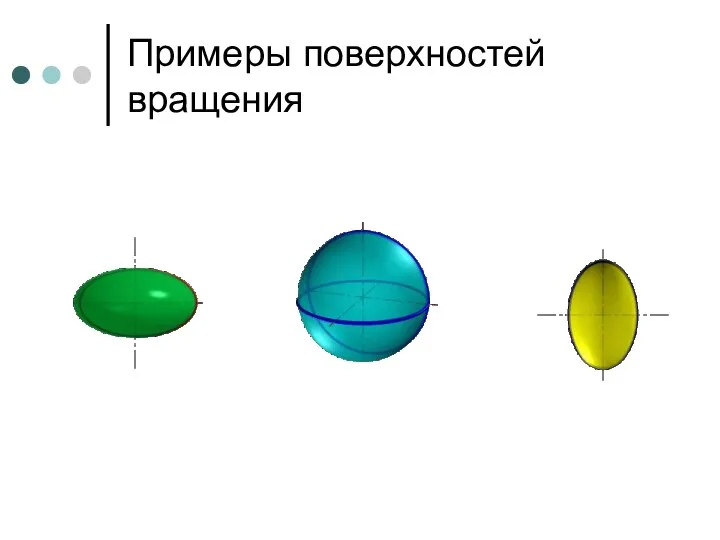
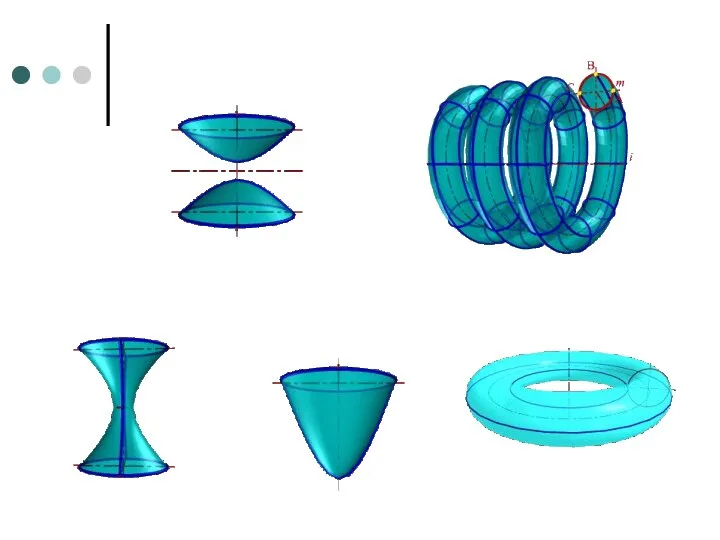
- 79. Примеры поверхностей вращения
- 80. Примеры косой плоскости
- 82. Поверхность Поверхностью называется совокупность всех последовательных положений линий, непрерывно перемещающихся в пространстве. Следовательно, всякую поверхность можно
- 83. Поверхности разделяют: По закону образования - на закономерные и незакономерные. Закономерные задаются графически и аналитически, незакономерные
- 84. Поверхности на комплексном чертеже могут быть заданы: Проекциями направляющих и способом перемещения по ним образующих. Семейством
- 85. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ В зависимости от формы образующей и закона ее перемещения в пространстве поверхности можно разделить
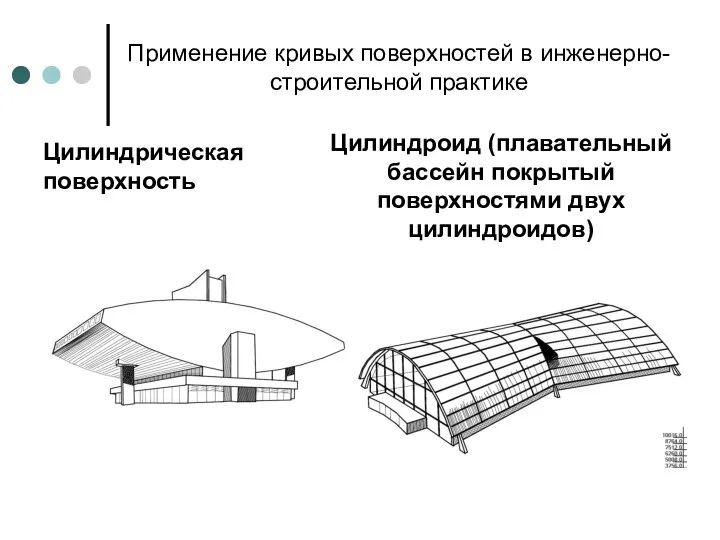
- 86. Применение кривых поверхностей в инженерно-строительной практике Цилиндрическая поверхность Цилиндроид (плавательный бассейн покрытый поверхностями двух цилиндроидов)
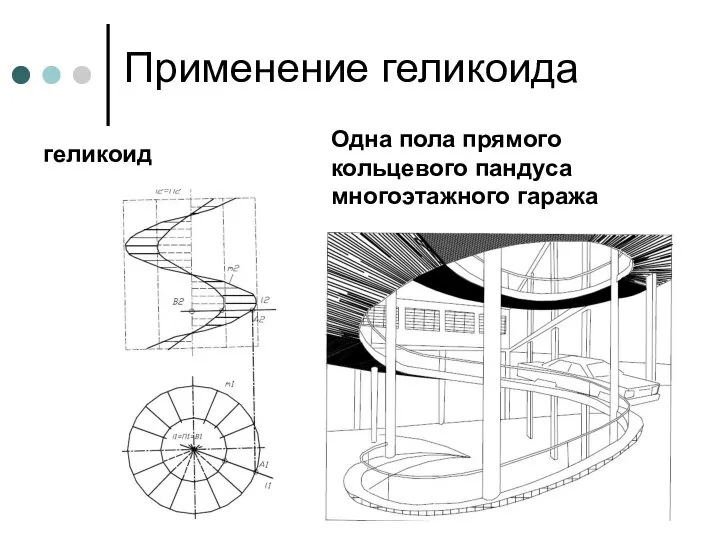
- 87. Применение геликоида геликоид Одна пола прямого кольцевого пандуса многоэтажного гаража
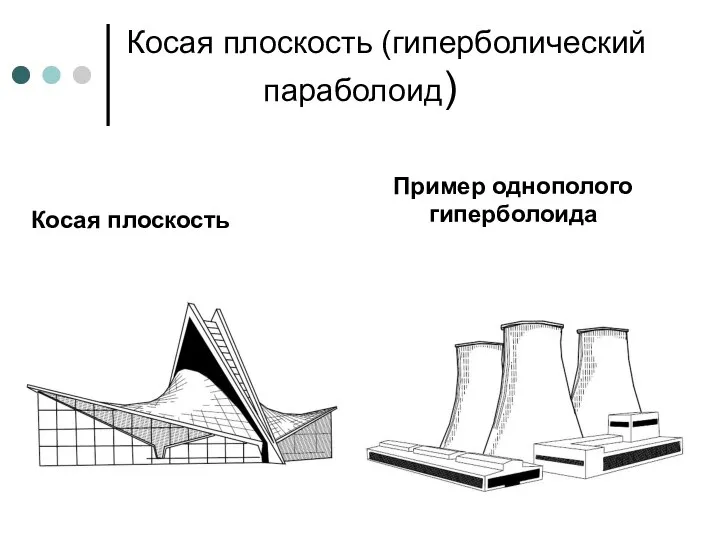
- 88. Косая плоскость (гиперболический параболоид) Косая плоскость Пример однополого гиперболоида
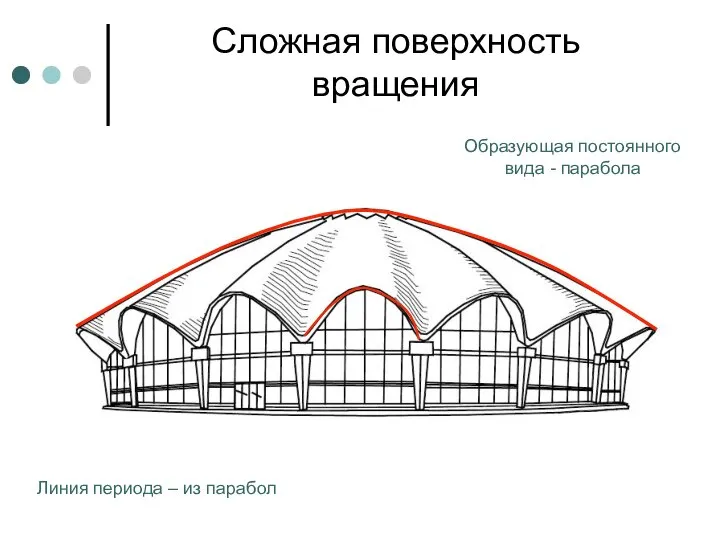
- 89. Сложная поверхность вращения Образующая постоянного вида - парабола Линия периода – из парабол
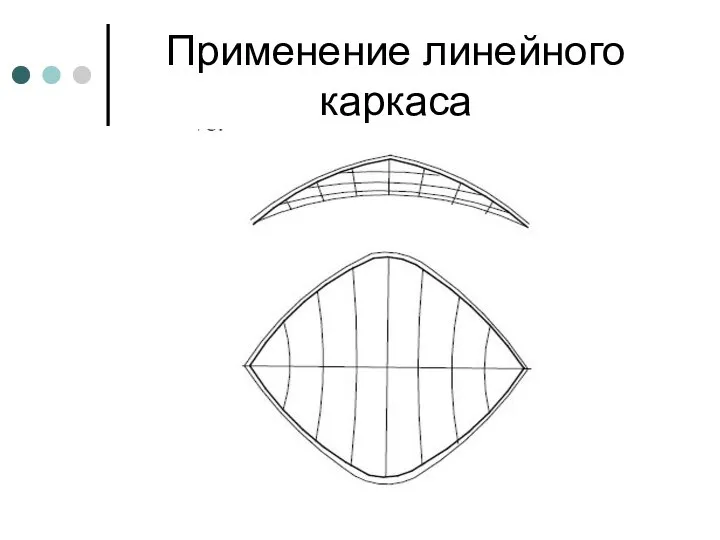
- 90. Применение линейного каркаса
- 91. Пример седловидного висячего покрытия
- 93. Скачать презентацию

























































 Презентация на тему Откуда в наш дом приходит электричество
Презентация на тему Откуда в наш дом приходит электричество  Как работает блокчейн (на примере криптовалюты)
Как работает блокчейн (на примере криптовалюты) Человек в политической жизни
Человек в политической жизни Пожары – страшное бедствие
Пожары – страшное бедствие Географическая координата
Географическая координата Презентация на тему Прощание с детским садом
Презентация на тему Прощание с детским садом Перестройка в СССР 1985-1991 гг.
Перестройка в СССР 1985-1991 гг. Презентация на тему Строение и свойства циклоалканов
Презентация на тему Строение и свойства циклоалканов  Презентация на тему Вооружение армии и флота РФ
Презентация на тему Вооружение армии и флота РФ Изменения в нормативной правовой базе ЕГЭ в 2012 г.
Изменения в нормативной правовой базе ЕГЭ в 2012 г. Презентация на тему Религиозные конфликты
Презентация на тему Религиозные конфликты  Архипов. Перезапуск DE
Архипов. Перезапуск DE Черное и белое
Черное и белое Презентация на тему Мудрая княгиня Ольга
Презентация на тему Мудрая княгиня Ольга  Презентация на тему Цветки и соцветия
Презентация на тему Цветки и соцветия  Опера Орфей и Эвридика (3 класс)
Опера Орфей и Эвридика (3 класс) Устройство компьютера
Устройство компьютера Партнерство B.Wave CC 1
Партнерство B.Wave CC 1 День открытых дверей
День открытых дверей Desert
Desert Протокол HTTP – основной транспорт Web
Протокол HTTP – основной транспорт Web Презентация на тему История Крыма
Презентация на тему История Крыма лол кек прикол
лол кек прикол William Shakespeare (23d of April 1564 – 23d of April 1616)
William Shakespeare (23d of April 1564 – 23d of April 1616) Климат моей квартиры
Климат моей квартиры Иллюзии восприятия
Иллюзии восприятия 2 Философия детско-массового футбола-FIFA Grassroots
2 Философия детско-массового футбола-FIFA Grassroots Этика и деонтология медработника при уходе за детьми
Этика и деонтология медработника при уходе за детьми