Содержание
- 2. Обобщенная математическая модель системы мониторинга Математическая модель детерминированного процесса единого закона динамики старения Входным сигналом системы
- 3. Обобщенная математическая модель системы мониторинга Математическая модель детерминированного процесса единого закона динамики старения Входным сигналом системы
- 5. – детерминированный закон старения объекта, выражающий долю израсходованного запаса работоспособности : – доля остаточного (неизрасходованного) запаса
- 6. – детерминированный закон старения объекта, выражающий долю израсходованного запаса работоспособности : – доля остаточного (неизрасходованного) запаса
- 7. – детерминированный закон старения объекта, выражающий долю израсходованного запаса работоспособности : – доля остаточного (неизрасходованного) запаса
- 8. где – начальный уровень, или начальный запас работоспособности по i-му параметру. критериальные функции скорости потери работоспособности
- 9. где – начальный уровень, или начальный запас работоспособности по i-му параметру. критериальные функции скорости потери работоспособности
- 10. где – начальный уровень, или начальный запас работоспособности по i-му параметру. критериальные функции скорости потери работоспособности
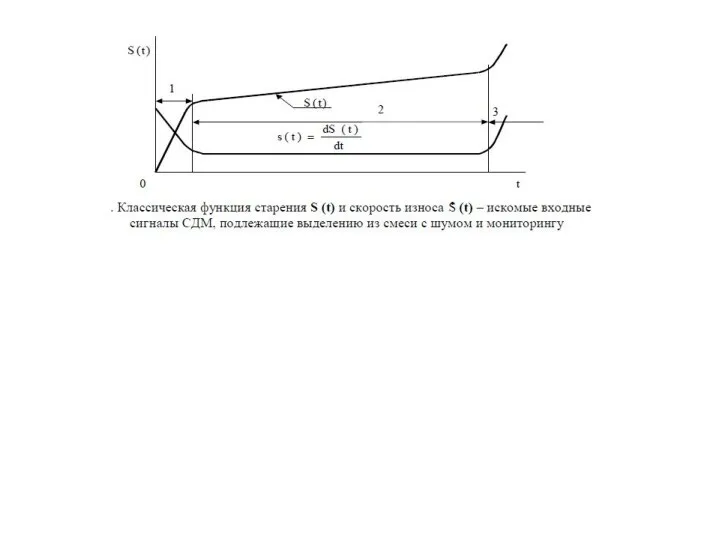
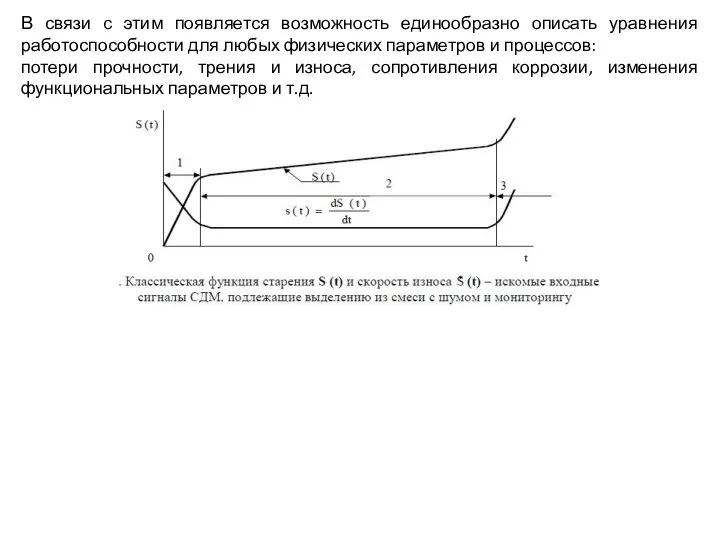
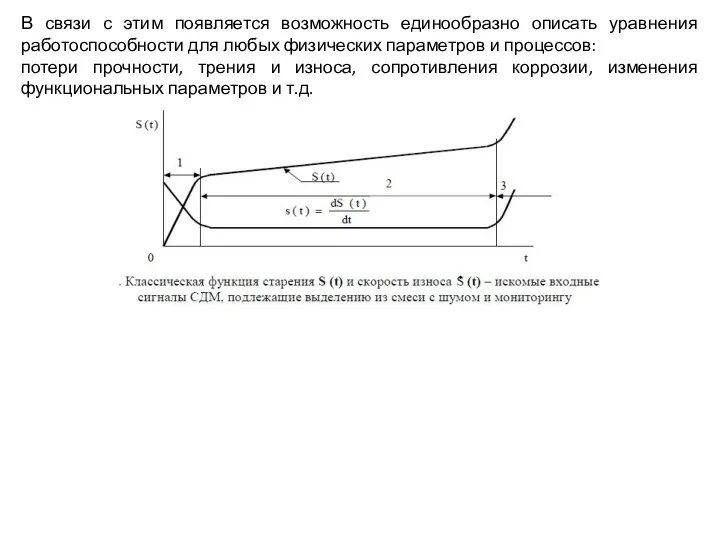
- 11. В связи с этим появляется возможность единообразно описать уравнения работоспособности для любых физических параметров и процессов:
- 12. В связи с этим появляется возможность единообразно описать уравнения работоспособности для любых физических параметров и процессов:
- 13. В связи с этим появляется возможность единообразно описать уравнения работоспособности для любых физических параметров и процессов:
- 14. В связи с этим появляется возможность единообразно описать уравнения работоспособности для любых физических параметров и процессов:
- 15. Бинарные уравнения работоспособности и старения имеют вид: – весовые коэффициенты;
- 16. Бинарные уравнения работоспособности и старения имеют вид: – весовые коэффициенты; распределение Вейбулла - Гнеденко с параметрами
- 17. Бинарные уравнения работоспособности и старения имеют вид: – весовые коэффициенты; распределение Вейбулла - Гнеденко с параметрами
- 18. Блок-схема обобщенной модели системы мониторинга состояния агрегатов Диагностика, как единовременный акт, оценивает остаточную работоспособность агрегатов в
- 19. Блок-схема обобщенной модели системы мониторинга состояния агрегатов Диагностика, как единовременный акт, оценивает остаточную работоспособность агрегатов в
- 20. Блок-схема обобщенной модели системы мониторинга состояния агрегатов Диагностика, как единовременный акт, оценивает остаточную работоспособность агрегатов в
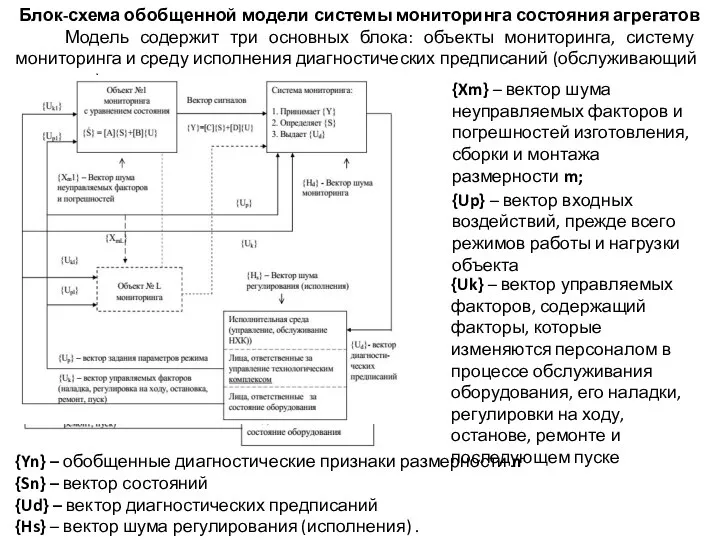
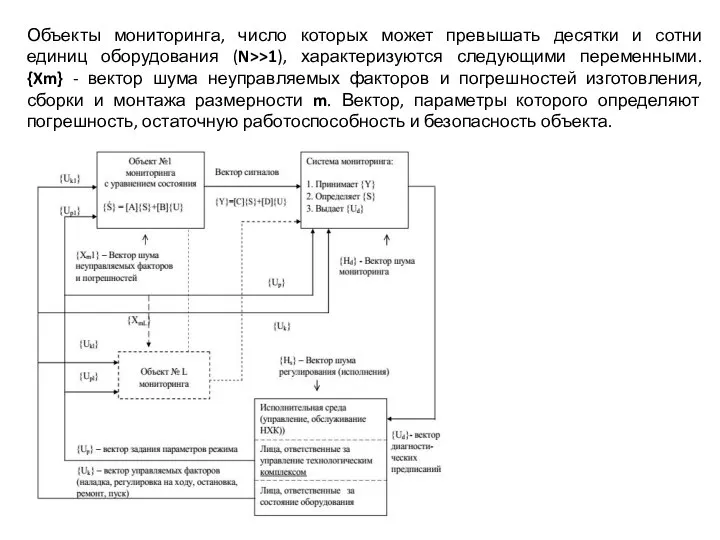
- 21. Блок-схема обобщенной модели системы мониторинга состояния агрегатов Модель содержит три основных блока: объекты мониторинга, систему мониторинга
- 22. Объекты мониторинга, число которых может превышать десятки и сотни единиц оборудования (N>>1), характеризуются следующими переменными. {Xm}
- 23. Объекты мониторинга, число которых может превышать десятки и сотни единиц оборудования (N>>1), характеризуются следующими переменными. {Xm}
- 24. {Up} - вектор входных воздействий, прежде всего режимов работы и нагрузки объекта. Например, для насосного агрегата
- 25. Вся совокупность переменных {Xm}, {Up} и {Uk} отображается через обобщенные координаты объекта диагностики и порождает обобщенные
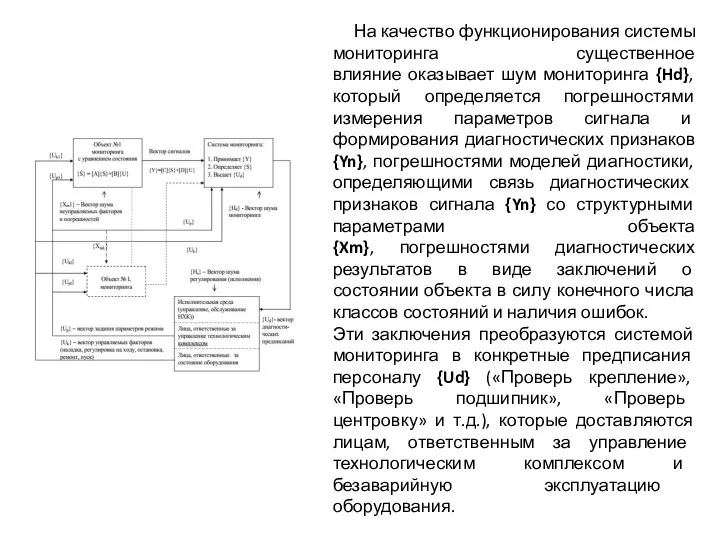
- 26. На качество функционирования системы мониторинга существенное влияние оказывает шум мониторинга {Hd}, который определяется погрешностями измерения параметров
- 27. Ясно, что решение о соответствующих работах с объектом мониторинга, находящимся в критическом состоянии и требующим внимания,
- 28. Оценка ошибки системы диагностики и мониторинга Применение стационарных систем диагностики и мониторинга позволяет перевести отказы технологических
- 29. Оценка ошибки системы диагностики и мониторинга Применение стационарных систем диагностики и мониторинга позволяет перевести отказы технологических
- 30. Оценка ошибки системы диагностики и мониторинга Применение стационарных систем диагностики и мониторинга позволяет перевести отказы технологических
- 31. Применение СДМ создает временную избыточность для действий персонала в условиях надвигающегося отказа, наблюдение за условиями возникновения
- 32. Применение СДМ создает временную избыточность для действий персонала в условиях надвигающегося отказа, наблюдение за условиями возникновения
- 33. б). Для того же примера интервал между производственными неполадками и аварийными ситуациями возрастает в 24 раза,
- 34. Параметры системы мониторинга: а)-допустимая ошибка η при требуемом риске r и фактической вероятности отказа – Q;
- 35. б)-коэффициент увеличения наработки между внезапными отказами при внедрении мониторинга и обеспечении требуемого риска отказа r;
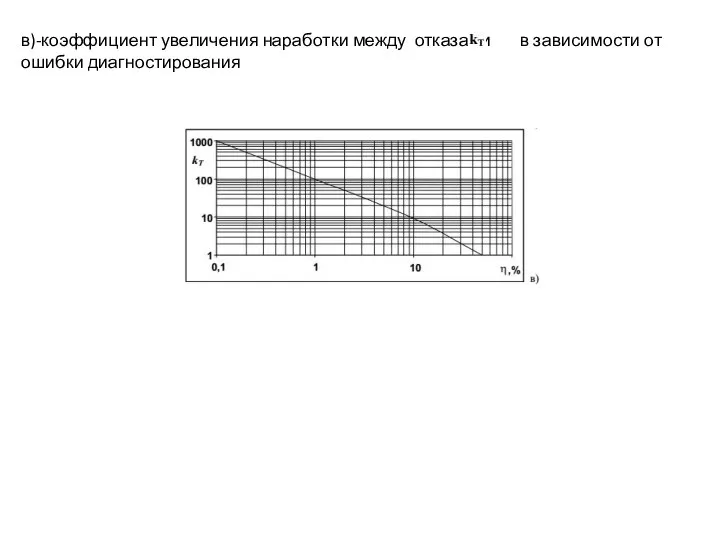
- 36. в)-коэффициент увеличения наработки между отказами в зависимости от ошибки диагностирования
- 37. Оценки изменения диагностических признаков При вибродиагностике нас интересуют не абсолютные координаты звеньев механизмов, а их погрешности
- 38. Оценки изменения диагностических признаков При вибродиагностике нас интересуют не абсолютные координаты звеньев механизмов, а их погрешности
- 39. Математическая модель системы мониторинга Чем больше погрешности или отклонения от номинального диапазона режимов работы, тем большие
- 40. где {Sm(t)} – вектор функций старения агрегата размерности m, каждая составляющая которого характеризует его обобщенный (совокупный)
- 41. где {Sm(t)} – вектор функций старения агрегата размерности m, каждая составляющая которого характеризует его обобщенный (совокупный)
- 42. Матрицы [А], [В], [С], [D] определяются следующим образом: [m, m] – квадратная матрица системы , которая
- 43. Для вибродиагностики матрица D определяет влияние на параметры вибрации агрегата действий персонала – изменения режима работы
- 44. Составляющие , как правило, недоступны для непосредственного наблюдения, что заставляет использовать методы косвенных измерений и диагностики.
- 45. Связь между приращением сигнала и приращением износа Необходимо заметить, что размерности пространства погрешностей m и пространства
- 46. Связь между приращением сигнала и приращением износа Необходимо заметить, что размерности пространства погрешностей m и пространства
- 47. Связь между приращением сигнала и приращением износа Необходимо заметить, что размерности пространства погрешностей m и пространства
- 48. Рассмотрим связь между приращением сигнала и приращением износа на интервале между управляющими воздействиями, когда : Полагая
- 49. Решая (1.18)-(1.20) относительно технического состояния объекта мониторинга, получим:
- 50. Решая (1.18)-(1.20) относительно технического состояния объекта мониторинга, получим: Соотношения (1.21) показывают, что предельное состояние агрегата и
- 51. Решая (1.18)-(1.20) относительно технического состояния объекта мониторинга, получим: Соотношения (1.21) показывают, что предельное состояние агрегата и
- 52. Уравнения (1.21)-(1.22) полностью определяют состояние объекта мониторинга через тренды диагностических признаков и их скорости. Техническое состояние
- 53. Уравнения (1.21)-(1.22) полностью определяют состояние объекта мониторинга через тренды диагностических признаков и их скорости. Техническое состояние
- 54. Уравнения (1.21)-(1.22) полностью определяют состояние объекта мониторинга через тренды диагностических признаков и их скорости. Техническое состояние
- 55. Уравнения (1.21)-(1.22) полностью определяют состояние объекта мониторинга через тренды диагностических признаков и их скорости. Техническое состояние
- 57. Скачать презентацию

































![Матрицы [А], [В], [С], [D] определяются следующим образом: [m, m] – квадратная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1111640/slide-41.jpg)













 Инструментальные средства для работы в системе Moodle
Инструментальные средства для работы в системе Moodle Семья в историческом интерьере
Семья в историческом интерьере Устойчивость транспортных потоков Евразии
Устойчивость транспортных потоков Евразии Составление уравнения по условию задачи6 класс
Составление уравнения по условию задачи6 класс КОНСТРУЦИОННЫЕ СТАЛИ
КОНСТРУЦИОННЫЕ СТАЛИ Классификация коньяка
Классификация коньяка  Как готовить системных программистов
Как готовить системных программистов Физминутка Крошка Енот
Физминутка Крошка Енот Вектора
Вектора Tag-questions (разделительные вопросы)
Tag-questions (разделительные вопросы)  Макет комнаты подростка
Макет комнаты подростка Школа
Школа День эффективности HR08 Апреля, 2011. Москва.
День эффективности HR08 Апреля, 2011. Москва. Писатель-романтик А.С. Грин Когда дни начинают пылиться и краски блекнуть, я беру Грина. Когда дни начинают пылиться и краски блекну
Писатель-романтик А.С. Грин Когда дни начинают пылиться и краски блекнуть, я беру Грина. Когда дни начинают пылиться и краски блекну Информатика и ИКТ
Информатика и ИКТ Орфография. Морфемика. Словообразование
Орфография. Морфемика. Словообразование Работа и мощность постоянного тока. Закон Джоуля-Ленца.
Работа и мощность постоянного тока. Закон Джоуля-Ленца. О Компании Роснефть и ОЦО – Общем Центре Обслуживания
О Компании Роснефть и ОЦО – Общем Центре Обслуживания Гравийно-песчаные заводы
Гравийно-песчаные заводы Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  10 принципов хорошего управления проектами в компаниях сферы услугВита Кравчук, управляющий партнер компании Business.People Киев, 1 ок
10 принципов хорошего управления проектами в компаниях сферы услугВита Кравчук, управляющий партнер компании Business.People Киев, 1 ок МЕТОДЫ ХРАНЕНИЯ ИЕРАРХИЧЕСКИХ СТРУКТУР В РЕЛЯЦИОННЫХ БАЗАХ ДАННЫХ
МЕТОДЫ ХРАНЕНИЯ ИЕРАРХИЧЕСКИХ СТРУКТУР В РЕЛЯЦИОННЫХ БАЗАХ ДАННЫХ Достопримечательности Омска
Достопримечательности Омска Инвестиционная политика предприятия в современных условиях
Инвестиционная политика предприятия в современных условиях Презентация_шаблон
Презентация_шаблон Презентация на тему Изобразительное искусство России второй половины XIX века
Презентация на тему Изобразительное искусство России второй половины XIX века  Минералы-индикаторы метапелитов
Минералы-индикаторы метапелитов Методика планирования воспитательной работы в классе
Методика планирования воспитательной работы в классе