Представление информации в памяти ЭВМ

Системы счисления
Число – это некоторая величина
Система счисления – это способ записи чисел с помощью цифр
Непозиционная –
количественный эквивалент
(«вес») цифры
не зависит от её
положения в записи числа
Позиционная –
количественный эквивалент
(«вес») цифры зависит от её положения
в записи числа
444
CDXLIV

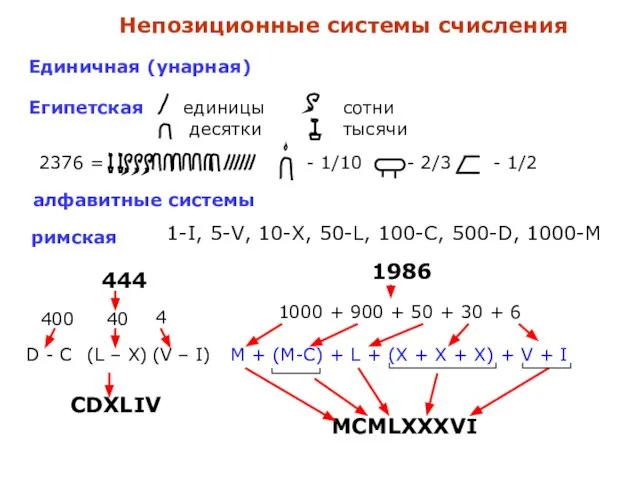
алфавитные системы
Единичная (унарная)
Непозиционные системы счисления
Египетская
римская
1-I, 5-V, 10-X, 50-L, 100-C, 500-D, 1000-M
М + (М-С) + L + (X + X + X) + V + I

Десятичная, двоичная, восьмеричная, шестнадцатеричная и др.
Основные достоинства любой позиционной системы
1. Простота выполнения арифметических действий
2. Ограниченное количество символов, необходимых
для записи числа
Позиционные системы счисления
Индийская мультипликативная система
Х – десятки
Y - сотни
Любое число в любой системе счисления можно представить с помощью развёрнутой формулы числа:
А – само число
g - основание системы счисления
a - цифры данной системы счисления
n - число разрядов целой части числа
m - число разрядов дробной части числа

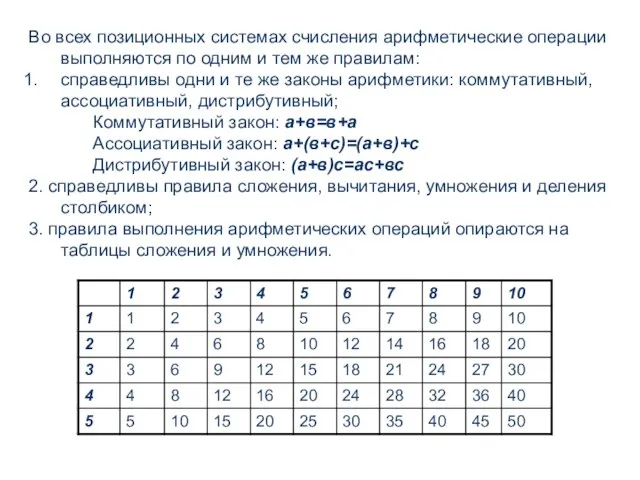
Во всех позиционных системах счисления арифметические операции выполняются по одним и тем же правилам:
справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;
Коммутативный закон: а+в=в+а
Ассоциативный закон: а+(в+с)=(а+в)+с
Дистрибутивный закон: (а+в)с=ас+вс
2. справедливы правила сложения, вычитания, умножения и деления столбиком;
3. правила выполнения арифметических операций опираются на таблицы сложения и умножения.

Перевод чисел из любой системы счисления
в десятичную
Алгоритм
1. Представить число в развёрнутой форме. При этом
основание системы счисления должно быть
представлено в десятичной системе счисления
2. Найти сумму ряда. Полученное число является
значением числа в десятичной системе счисления
Пример: 11012 → А10
11012 =1·23 +1·22 +0 ·21 +1 ·20
23 +22 +0 +20 =8+4+0+1 = 1310
Перевести в десятичную систему числа:
11112
11115
11113
=1510
=15610
=4010
Задание:

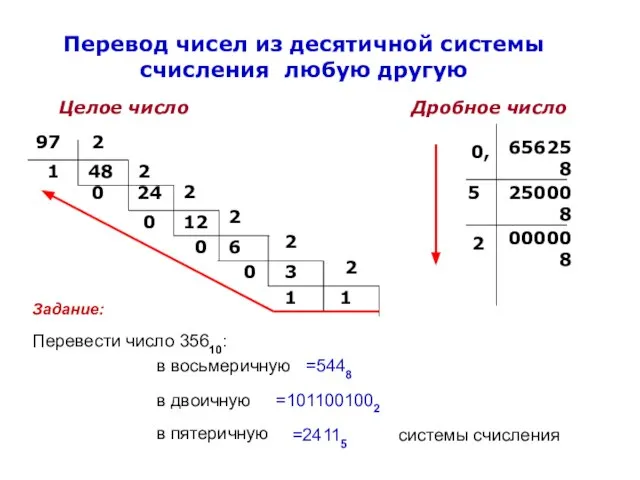
Перевод чисел из десятичной системы счисления любую другую
Целое число
Дробное число
Перевести число 35610:
в восьмеричную
в двоичную
в пятеричную
системы счисления
=5448
=1011001002
=24115
Задание:

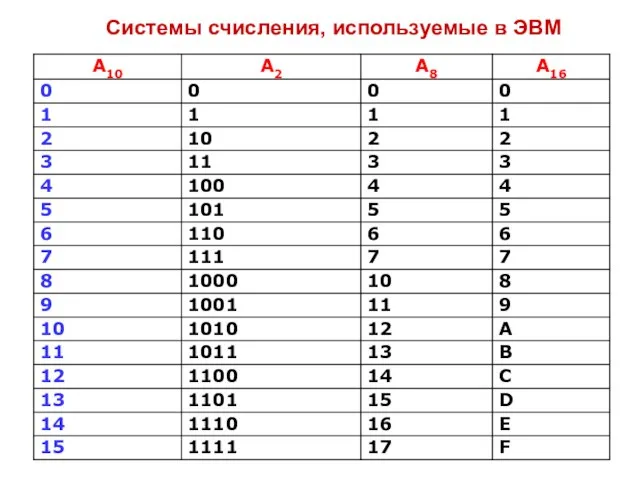
Системы счисления, используемые в ЭВМ

Системы счисления, используемые в ЭВМ (с основанием 2m)
Используя таблицу, перевести:
1. 100011010110012 → А8 → А16
2. 4АС216 → А2 → А8
3. 7138 → А2 → А16
= 215318 = 235916
= 1001010110000102 = 453028
= 1110010112 = 1СВ16
Алгоритм перевода целых двоичных чисел в сиcтемах счисления c основанием с основанием 2m
1. Двоичное число разбить справа налево на группы по n разрядов в каждой
2. Если в левой последней группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2n

Двоичная система счисления
Сложение
Вычитание
Умножение
Деление

Решить:
Произвести сложение, вычитание, умножение и деление двоичных чисел 10102 и 112
Сложить восьмеричные числа 58 и 48, 178 и 418
Сложить числа 102 и 48
Прочитать число: МMIX
Записать число 3974 в римской системе счисления
Ответы:
11012, 1112, 1001102, 112 и 1 в остатке.
2. 118, 608.
3. 1102
4. 2009
5. MMMCMLXXIV

Представление чисел в ЭВМ
Все числовые данные хранятся в памяти компьютера в двоичном виде, т. е. в виде последовательностей нулей и единиц, однако формы хранения целых и вещественных чисел различны.
Необходимость различного представления целых и вещественных чисел вызвана тем, что скорость выполнения операций над целыми числами существенно выше, чем над вещественными числами.
Текстовая, графическая, звуковая информация, количество деталей, акций, сотрудников – эти и многие другие данные выражаются целыми числами.
Для решения математических и физических задач, в которых невозможно обойтись только целыми числами, используются вещественные числа.
Решение проблем математического моделирования в естественных науках, экономике и технике, работа с САПР, электронными таблицами невозможна без использования вещественных (действительных) чисел.

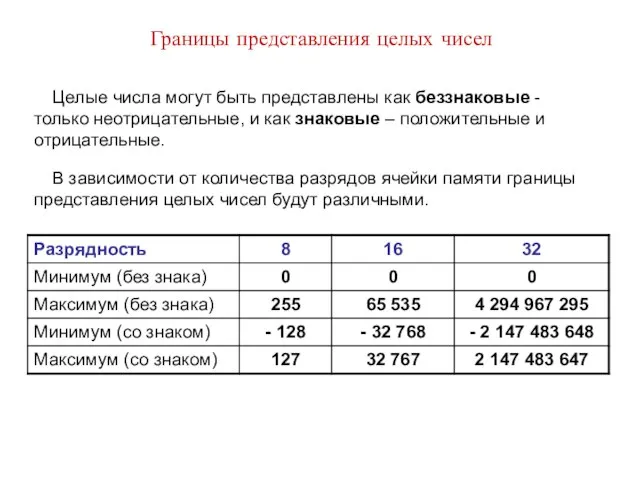
Границы представления целых чисел
Целые числа могут быть представлены как беззнаковые - только неотрицательные, и как знаковые – положительные и отрицательные.
В зависимости от количества разрядов ячейки памяти границы представления целых чисел будут различными.

Представление целых чисел
Целые числа, как знаковые, так и беззнаковые, хранятся в формате с фиксированной точкой.
При таком представлении чисел все разряды ячейки, кроме знакового, если он есть, служат для изображения разрядов числа.
Причем каждому разряду ячейки соответствует один и тот же разряд числа. Именно поэтому такое представление называется с фиксированной точкой, так как фиксируется место десятичной точки перед определенным разрядом.
Для целых чисел десятичная точка находится после младшего разряда, то есть вне разрядной сетки.

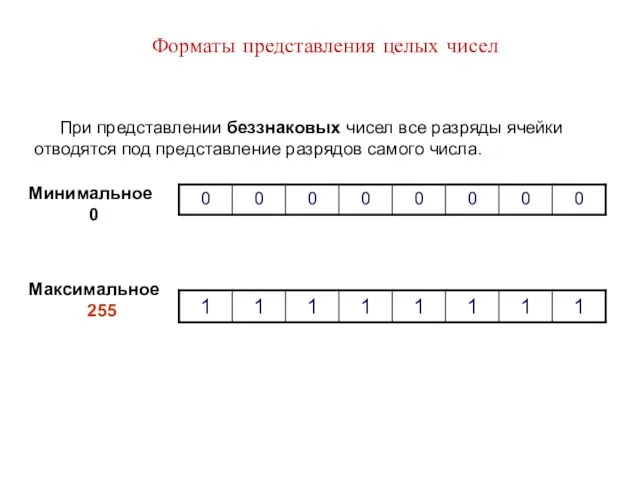
Форматы представления целых чисел
При представлении беззнаковых чисел все разряды ячейки отводятся под представление разрядов самого числа.
Минимальное
0
Максимальное
255

В случае представления знаковых целых чисел старший (левый) разряд ячейки отводится под хранение знака числа. В этот разряд заносится 0, если число положительное и 1 – если число отрицательное. Поскольку для хранения разрядов самого числа количество разрядов ячейки уменьшается на единицу, границы представления уменьшаются в два раза.
Почему минимальное знаковое число в 8-разрядной ячейке –128, а максимальное +127?
Максимальное знаковое число 127
Минимальное знаковое число -128

Прямой код числа
Представление в форме «знак» - «величина», когда старший разряд ячейки отводится под знак, называется прямым кодом двоичного числа.
Число 10012
Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке памяти машины.
Для получения обратного кода числа все значения инвертируются.
Дополнительный код = прямому коду.
Для положительного числа
Например: Дано число 10012. Записать его для 8-разрядной ячейки.
прямой код =
дополнительный код =

Дополнительный код
Число 243 в одном байте будет выглядеть так:
Число 24310
Но если эту запись рассматривать как запись числа со знаком, значением записи будет число -11510
Отрицательные целые числа представляются в ЭВМ с помощью дополнительного кода.
Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что значительно упрощает работу процессора и увеличивает его быстродействие.

Алгоритм получения дополнительного кода отрицательного числа в n двоичных разрядах:
Модуль числа записать в прямом коде в n двоичных разрядах.
Получить обратный код числа.
К полученному обратному коду прибавить единицу.
Например: записать дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления.
Прямой код: |-200210|=200210=00000111110100102
Обратный код: 11111000001011012
Дополнительный код: 11111000001011102
Дополнительный код отрицательного числа
+1
Дополнительный код отрицательного числа m =2k-|m|, где k – количество разрядов в ячейке, |m|< 2k.
Дополнительный код отрицательного числа – это дополнение |m| до 2k.

Нормализованная запись чисел
Вещественные (дробные) числа хранятся и обрабатываются в компьютере в формате с плавающей точкой. Формат чисел с плавающей точкой базируется на экспоненциальной форме записи, в которой может быть представлено любое число.
Недостатком представления чисел с фиксированной точкой является небольшой диапазон представляемых величин, недостаточный для решения математических, физических, экономических и других задач.
А=m*qn
Для единообразия представления чисел с плавающей точкой, используется нормализованная форма, при которой мантисса отвечает условию:
1/ n≤|m|<1
Это означает, что мантисса должна быть правильной дробью и иметь после запятой цифру отличную от нуля.

Примеры нормализации чисел:
3.1415926=0.31415926•101
1000=0.1•104
3) – 0.123456789= – 0.123456789 •100
4) 0.00001078=0.1078•8-4
5) 1000.00012=0.100000012 •24
6) – 0.00011012= – 0.11012 •2-3
Запись нуля считается нормализованной, если и мантисса, и порядок равны нулю, т. е. 0 = 0.0•100
Числа в формате с плавающей точкой занимают в памяти компьютера 4 (число обычной точности) или 8 байтов (число двойной точности).

знак порядка (+)
Компьютерное представление вещественных чисел
Как и для целых чисел, при представлении вещественных чисел используется двоичная система счисления, поэтому предварительно число должно быть переведено в двоичную систему.
При представлении чисел с плавающей точкой в разрядах ячейки отводится место для знака числа, знака порядка, абсолютной величины порядка, абсолютной величины мантиссы.
знак числа (-)
абсолютная величина порядка (13)
абсолютная величина мантиссы (5826486)
В ячейке записано отрицательное двоичное число –1011011000010.11110011
В десятичном представлении это будет число –5826.486