Презентация на тему Дедуктивное умозаключение

Мышление - это процесс обобщенного и опосредованного отражения действительности в её существенных связях и отношениях.
Мышление – открытие новых свойств и признаков объекта через включение его в новые связи.
Логика - наука, изучающая
законы и формы мышления,
способы рассуждений
и доказательств

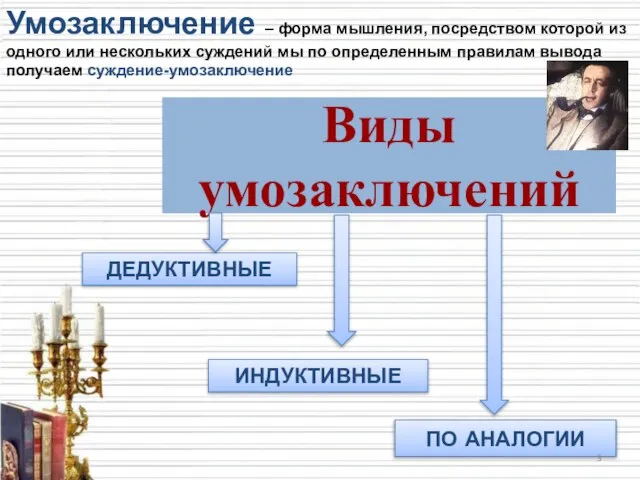
Виды умозаключений
ДЕДУКТИВНЫЕ
ИНДУКТИВНЫЕ
ПО АНАЛОГИИ
Умозаключение – форма мышления, посредством которой из одного или нескольких суждений мы по определенным правилам вывода получаем суждение-умозаключение

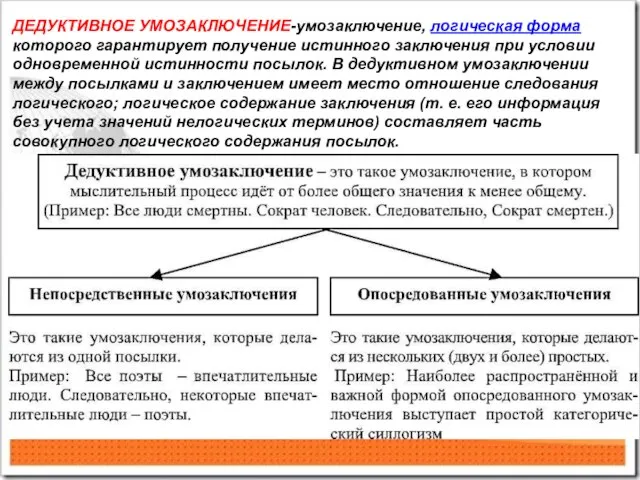
Виды умозаключений
ДЕДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ-умозаключение, логическая форма которого гарантирует получение истинного заключения при условии одновременной истинности посылок. В дедуктивном умозаключении между посылками и заключением имеет место отношение следования логического; логическое содержание заключения (т. е. его информация без учета значений нелогических терминов) составляет часть совокупного логического содержания посылок.

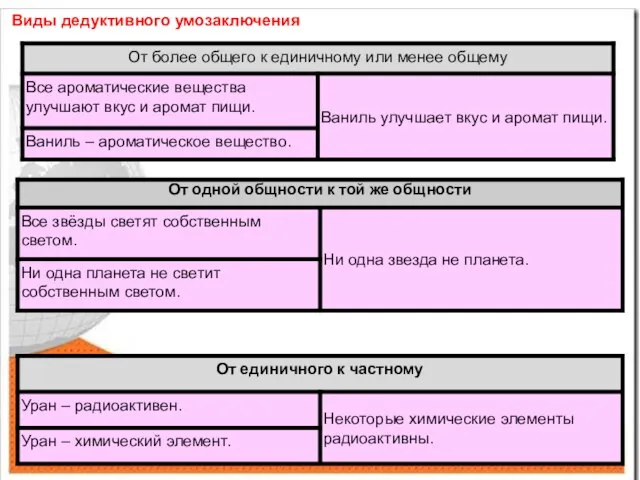
Виды дедуктивного умозаключения
.
Все звёзды светят собственным светом. Ни одна звезда не планета.

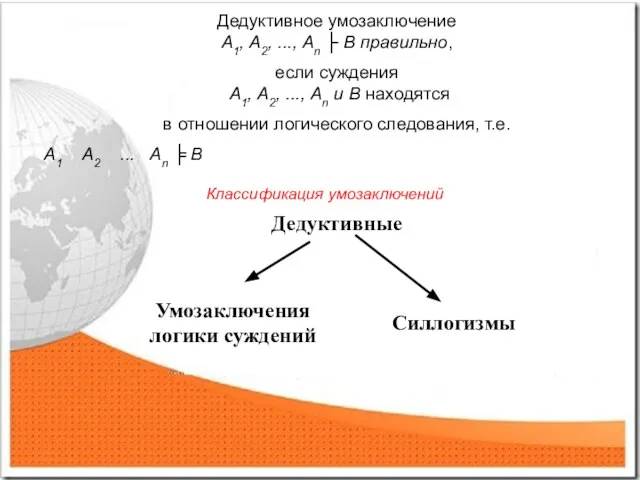
Дедуктивное умозаключение
А1, А2, ..., Аn ├ B правильно,
если суждения А1, А2, ..., Аn и В находятся
в отношении логического следования, т.е.
А1 А2 ... Аn ╞ B
Дедуктивные
Силлогизмы
Умозаключения логики суждений
Классификация умозаключений

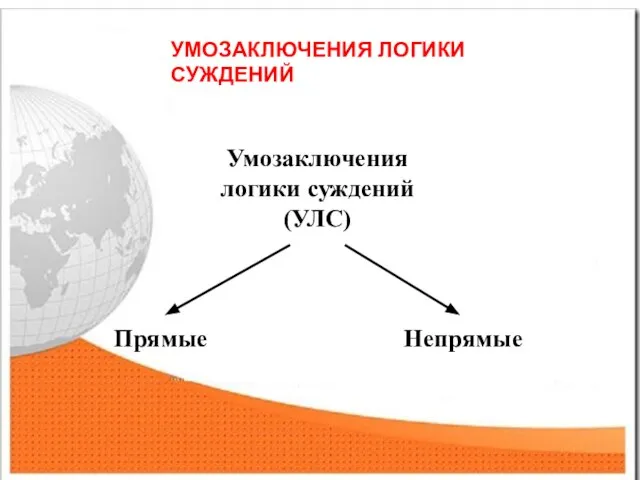
Умозаключения логики суждений
(УЛС)
Прямые
Непрямые
УМОЗАКЛЮЧЕНИЯ ЛОГИКИ СУЖДЕНИЙ

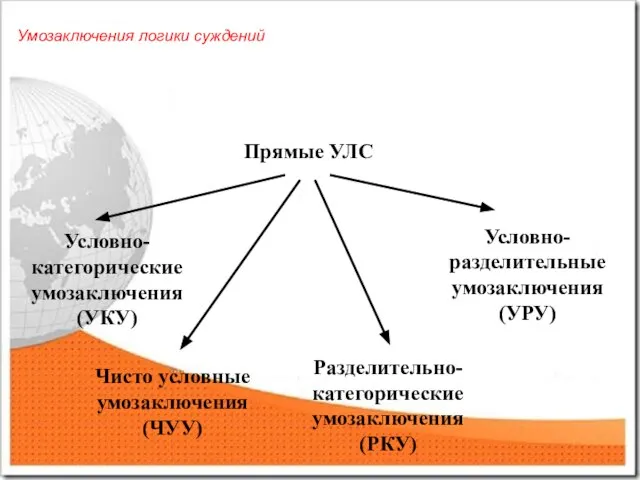
Прямые УЛС
Чисто условные умозаключения (ЧУУ)
Разделительно-категорические умозаключения (РКУ)
Условно-разделительные умозаключения (УРУ)
Условно-категорические умозаключения (УКУ)
Умозаключения логики суждений

Условно-категорическими называются умозаключения, в которых одна посылка – условное суждение,
а вторая посылка и заключение – импликанты этого суждения или их отрицания. Условно-категорическими называются умозаключения, в которых одна посылка – условное суждение,
а вторая посылка и заключение – импликанты этого суждения или их отрицания.
А→В
А – основание,
В – следствие,
А и В – импликанты.
А→В, А├ В
Умозаключения, совершаемые по схеме А→В, А├ В назовем умозаключениями
от утверждения основания к утверждению следствия
modus ponendo ponens (modus ponens)
А→В, В├ А
Умозаключения, совершаемые по схеме А→В, В├ А назовем умозаключениями
от отрицания следствия к отрицанию основания.
modus tollendo tollens (modus tollens)

Чисто условными называются умозаключения, в которых обе посылки и заключение представляют собой условные суждения.
А→В, B → C├ A →C
Пример:
Если студент хорошо занимается в течение семестра, то он хорошо сдает сессию.
Если студент хорошо сдает сессию, то он получает стипендию.
Следовательно:
если студент хорошо занимается во время семестра, то он получает стипендию.

Разделительно-категорическими умозаключениями
называются умозаключения, в которых одна посылка – разделительное суждение, а другая посылка и заключение – альтернативы этого суждения.
А, В – альтернативы суждения
AVB
Пример:
«Либо мы победим, либо все пойдет ко всем чертям! Но мы победим!»