Презентация на тему Динамика Масса и импульс тела Силы

Масса и импульс тела. Сила
Из опыта известно, что при одинаковых воздействиях различные тела приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы).
Опыт показывает, что любое тело противится попыткам изменить его состояние движения. Это свойство называют инертностью. Мерой инертности служит масса. Определение массы производят путем сравнения с эталоном. Масса тела m  скалярная физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства.
В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 1012 их значения).

Чтобы описывать воздействия, упоминаемые в первом законе Ньютона, вводят понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т. е. изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения.

Итак, сила  это векторная величина, являющаяся мерой механического действия на рассматриваемое тело со стороны других тел. Механическое взаимодействие может осуществляться как между контактирующими телами (например, при трении, при давлении тел друг на друга), так и между удаленными телами (через поля – гравитационные, электромагнитные и т.п.).

Все силы можно разделить на два основных типа:
силы, действующие при непосредственном соприкосновении
силы, которые действуют независимо от того, соприкасаются тела или нет, т. е. силы, которые могут действовать на расстоянии.
Для того чтобы одно тело могло действовать на другое при непосредственном соприкосновении, первое должно быть в особом состоянии: чтобы рука действовала на мяч, мышцы руки должны быть сокращены; чтобы действовать на пробку игрушечного пистолета, воздух или пружина должны быть сжаты, и т. д. Сжатия, растяжения, изгибы и т. п.— это изменения формы или объема тел по сравнению с их исходным состоянием. Такие изменения называют деформациями и при наличии таких изменений говорят, что тело деформировано. Мышцы, пружины, газ и т. п. должны находиться в деформированном состоянии, чтобы действовать на соприкасающиеся с ними тела с некоторой силой. Эти силы в большинстве случаев действуют только до тех пор, пока тела деформированы, и исчезают вместе с исчезновением деформаций. Такие силы называют упругими. Кроме упругих сил, при непосредственном соприкосновении могут возникать еще и силы трения.

Для сил, действующих на расстоянии, нет такой простой картины взаимодействия тел, как для упругих сил. Важнейший пример сил, действующих на расстоянии,— силы всемирного тяготения и, как частный случай, сила тяжести (сила земного притяжения). Падение тела, т. е. наличие ускорения, направленного вниз, у тела, поднятого над Землей и предоставленного самому себе, показывает, что со стороны Земли на него действует сила, хотя во время падения тело и не соприкасается с Землей.
Силы всемирного тяготения, действующие между предметами нашей обыденной жизни, ничтожны по сравнению с остальными силами, действующими между ними. Например, резиновая нить длиной в 1 м и поперечником в 1 мм, растянутая всего лишь на 1 мм, действует с силой упругости, в миллионы раз превосходящей силу взаимного тяготения между двумя килограммовыми гирями, стоящими на расстоянии 1 м друг от друга. Но если одно (или оба) из притягивающих тел — это огромное небесное тело, силы всемирного тяготения также делаются огромными. Так, Земля притягивает килограммовую гирю в 1000 раз сильнее, чем притягиваются гири в приведенном примере, а Солнце притягивает Землю в 4*1021 раз сильнее, чем Земля притягивает гирю.

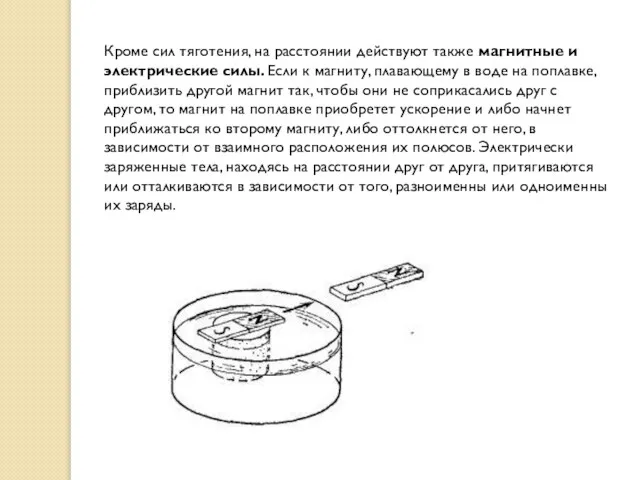
Кроме сил тяготения, на расстоянии действуют также магнитные и электрические силы. Если к магниту, плавающему в воде на поплавке, приблизить другой магнит так, чтобы они не соприкасались друг с другом, то магнит на поплавке приобретет ускорение и либо начнет приближаться ко второму магниту, либо оттолкнется от него, в зависимости от взаимного расположения их полюсов. Электрически заряженные тела, находясь на расстоянии друг от друга, притягиваются или отталкиваются в зависимости от того, разноименны или одноименны их заряды.

Если на рассматриваемое тело действует несколько сил, то его поступательное движение будет таким же, как если бы на тело действовала результирующая сила, равная векторной сумме отдельных сил:
Последнее выражение определяет принцип суперпозиции для сил.
Группу рассматриваемых тел называют системой тел. Силы взаимодействия между телами, входящими в систему, называют внутренними. Силы, действующие на тела, входящие в систему, со стороны тел, не входящих в систему, называют внешними.
Систему называют замкнутой (изолированной), если на нее не действуют внешние силы.
Сила не нуждается в ругательствах.
Достоевский Ф. М.
Сила всегда привлекает людей с низкими моральными качествами.
А.Эйнштейн

Согласно многочисленным опытам можно отметить следующие закономерности. Под действием силы материальная точка изменяет свою скорость не мгновенно, а постепенно, т.е. приобретает конечное по величине ускорение, которое тем меньше, чем больше масса материальной точки.
Если два тела с разными массами m1 и m2 испытывают одинаковые воздействия (F1= F2), то тела движутся с ускорениями, обратно пропорциональными их массам:
Таким образом, сравнение масс двух тел, на которые действует одна та же сила, сводится к сравнению ускорений этих тел.
Взяв некоторое тело за эталон массы, можно сравнивать массу любого тела с этим эталоном. В физике в качестве основной единицы массы принят килограмм. Килограмм есть масса эталонной гири из платиноиридиевого сплава, хранящейся в Севре (Франция) в Международном бюро мер и весов.

В классической механике выделяют два свойства массы:
масса – величина аддитивная, т.е. масса тела равна сумме масс его составных частей;
масса – величина постоянная и не зависит от характера движения тела.
В релятивистской механике масса m зависит от скорости v согласно формуле:
где c  скорость света в вакууме, m0  постоянная для данной частицы величина, называемая ее массой покоя.
Масса покоя совпадает с массой, рассматриваемой в классической механике.

Импульсом или количеством движения называют произведение массы тела на его скорость:
Импульсом системы материальных точек называют векторную сумму импульсов отдельных материальных точек, из которых эта система состоит:

Второй закон Ньютона
Второй закон Ньютона  основной закон динамики поступательного движения. Он отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело силе:
Это уравнение называют уравнением движения тела.
Заменив импульс произведением mv и учитывая, что в классической механике масса остается постоянной, можно представить gjcktlytt соотношение в виде:
Таким образом, мы пришли к другой формулировке второго закона Ньютона: произведение массы тела на его ускорение равно действующей на тело силе.

Единица силы в СИ  ньютон (Н): 1 Н  сила, которая массе в 1 кг сообщает ускорение 1 м/с2 в направлении действия силы: 1 Н = 1 кгм/с2.
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго.
Действительно, в случае равенства нулю равнодействующей силы (при отсутствии воздействия на тело со стороны других тел) ускорение также равно нулю. Однако первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно он утверждает существование инерциальных систем отсчета.
В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было.
В своих трудах «Математические начала натуральной философии», Исаак Ньютон приводит следующую формулировку своего закона:
“Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует”.

Третий закон Ньютона
Механическое воздействие тел друг на друга носит характер их взаимодействия: если тело 1 действует на тело 2 с некоторой силой , то и тело 2 в свою очередь действует на тело 1 с такой же силой силой . Третий закон Ньютона утверждает, что силы взаимодействия двух материальных точек равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей эти точки:
При использовании законов динамики иногда допускают следующую ошибку: так как действующая сила всегда вызывает равную по модулю и противоположную по направлению силу противодействия, то, следовательно, их равнодействующая должна быть равна нулю и тела вообще не могут приобрести ускорения.
На самом деле третий закон Ньютона говорит о равенстве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение.

Исаак Ньютон (1643 — 1727 )
Английский математик, астроном, физик, механик, заложивший основы классической механики, он объяснил движение небесных тел – планет вокруг Солнца и Луны вокруг Земли. Самым известным его открытием был закон всемирного тяготения.
Исаак Ньютон родился 4 января 1643 года в небольшой деревушке Вулсторп в графстве Линкольншир. Отец его умер еще до рождения сына, а мать, выйдя замуж во второй раз, оставила Ньютона на попечении бабушки. Он рос необщительным мальчиком, поначалу в школе учился очень плохо и часто становился объектом для насмешек одноклассников. Но упорство в учении позволило ему вскоре стать одним из успевающих учеников, и отношение к нему изменилось.
Больше всего Ньютона интересовала техника и математика. В 1660 году Ньютон поступил в Кембридж, который окончил в 1665 году со званием магистра искусств. Он стал всерьез заниматься наукой.
«Фантазия усиливается пребыванием на свежем воздухе, постом, умеренным потреблением вина, но портится от пьянства, разврата и слишком усердного учения».
Исаак Ньютон

В 1665-67 гг., во время эпидемии чумы, он жил в своей родной деревне Вулсторп. Эти годы вынужденного затворничества оказались наиболее продуктивными в его научном творчестве.
В это время у Ньютона сложились идеи, которые привели его к созданию дифференциального и интегрального исчислений, изобретению зеркального телескопа (собственноручно изготовленного им в 1668 г.), открытию закона всемирного тяготения. Здесь он провёл опыты по разложению (дисперсии) света.
В 1687 г. он опубликовал свой грандиозный труд "Математические начала натуральной философии" ("Начала").
Открытые Ньютоном основы механики всех физических тел и явлений – от небесных тел до распространения звука - определили развитие физики как науки на много веков вперед. Научное творчество Ньютона сыграло исключительно важную роль в истории развития физики. В его честь названа единица силы в Международной системе единиц – ньютон. Сам Ньютон достаточно скромно отзывался о своих открытиях, считая их подготовленными его предшественниками. Широко известна его фраза: «Если я видел дальше других, то потому, что стоял на плечах гигантов».

Эпитафия
Ньютон умер в 1727 г. в Кенсингтоне и был похоронен в английском национальном пантеоне - Вестминстерском аббатстве.
На его могиле высечено:
"Здесь покоится Сэр Исаак Ньютон
Который почти божественной силой своего ума
Впервые объяснил
С помощью своего математического метода
Движения и формы планет,
Пути комет, приливы и отливы океана.
Он первый исследовал разнообразие световых лучей
И проистекающие отсюда особенности цветов,
Каких до того времени никто даже не подозревал.
Прилежный, проницательный и верный истолкователь
Природы, древностей и священного писания,
Он прославил в своем учении Всемогущего Творца.
Требуемую Евангелием простоту он доказал своей жизнью.
Пусть смертные радуются, что в их среде
Жило такое украшение человеческого рода.
Родился 25 декабря 1642 г.
Умер 20 марта 1727 года

Упругие силы
Абсолютно твердое тело  это такое тело, которое ни при каких условиях не может деформироваться. В абсолютно твердом теле при всех условиях расстояние между двумя произвольными точками остается неизменным. Все реальные тела при определенных условиях деформируются, т.е. тем или иным образом изменяют свою форму и размеры.
В случае твердых тел различают два предельных случая: упругие деформации и пластические деформации.
Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными).
Характер деформации (упругая или пластическая) зависит как от материала тела, так и от величины внешнего воздействия. Мы ограничимся изучением только упругих деформаций изотропных тел. Изотропными называются тела, свойства которых одинаковы по всем направлениям.

Рассмотрим однородный стержень длиной l0 и площадью поперечного сечения S и приложим к его основаниям растягивающие или сжимающие силы F, в результате чего длина стержня меняется на величину l. Естественно, что при растяжении l положительно, а при сжатии  отрицательно.
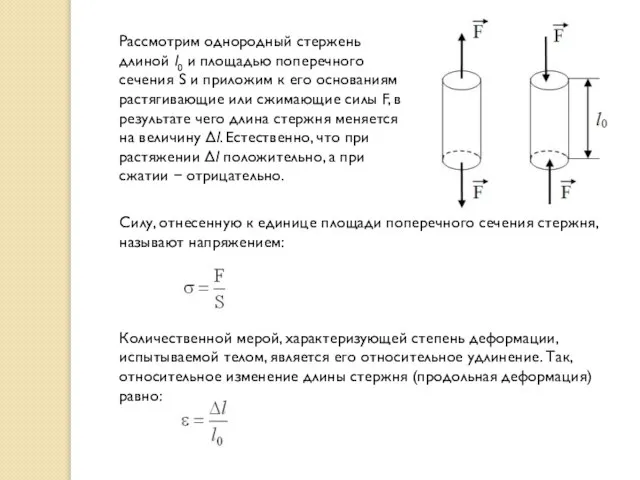
Силу, отнесенную к единице площади поперечного сечения стержня, называют напряжением:
Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительное удлинение. Так, относительное изменение длины стержня (продольная деформация) равно:

Английский физик Р. Гук (16351703) экспериментально установил, что для малых деформаций относительное удлинение  и напряжение  прямо пропорциональны друг другу(закон Гука):
где коэффициент пропорциональности Е называется модулем Юнга.
Из последнего выражения видно, что модуль Юнга (модуль упругости) численно равен напряжению, вызывающему относительное удлинение, равное единице. Поэтому модуль Юнга часто определяют как напряжение, которое необходимо приложить к стержню, чтобы его длина удвоилась (если бы при такой деформации закон Гука оставался еще верным).
Недостаток этого определения состоит в том, что при таких больших деформациях закон Гука почти для всех тел становится недействительным: тело либо разрушается, либо нарушается пропорциональность между деформацией и приложенным напряжением.

Роберт Гук (1635- 1703)-
английский физик, астроном, ботаник и изобретатель, один из создателей и деятельный член Лондонского королевского общества, его секретарь в 1677-83 гг., профессор Лондонского университета.
Р. Гук, разносторонний ученый и экспериментатор, сделал ряд крупнейших физических открытий (закон деформации упругого тела, теория упругости, волновая теория света и др.). Заинтересовавшись оптической новинкой XVII в. – микроскопом – он реконструировал этот прибор. Микроскопические наблюдения исследователя изложены им в труде "Микрография, или некоторые физиологические описания мельчайших тел, осуществленные посредством увеличительных стекол" (1665 г.). Рассматривая самые разнообразные объекты из мертвой и живой природы, Р. Гук, в частности, открывает клеточное строение растений; он является и автором термина "клетка", вошедшего со временем в научный обиход.

Томас Юнг (1773 - 1829) - английский ученый, один из создателей волновой оптики и теории упругости.
С ранних лет обнаружил необыкновенные
способности
и феноменальную память. В 2 года научился бегло
читать, в 4 знал на память много сочинений английских поэтов, в 8-9 лет овладел токарным ремеслом и мастерил различные физические приборы, к 14 годам познакомился с дифференциальным исчислением (по Ньютону), изучил много языков (греческий, латынь, французский, итальянский, арабский и др.).
Его работы относятся к оптике, акустике, теплоте, механике, математике, астрономии, геофизике, филологии, зоологии. Объяснил явление аккомодации глаза изменением кривизны хрусталика. Впервые указал на усиление и ослабление звука при наложении звуковых волн (интерференция звука) и предложил принцип суперпозиции волн.
В теории упругости Юнгу принадлежат исследования деформации сдвига, он впервые ввел характеристику упругости - модуля растяжения (модуль Юнга).

Закон Гука может быть записан также в виде
где k  коэффициент упругости (жесткости).
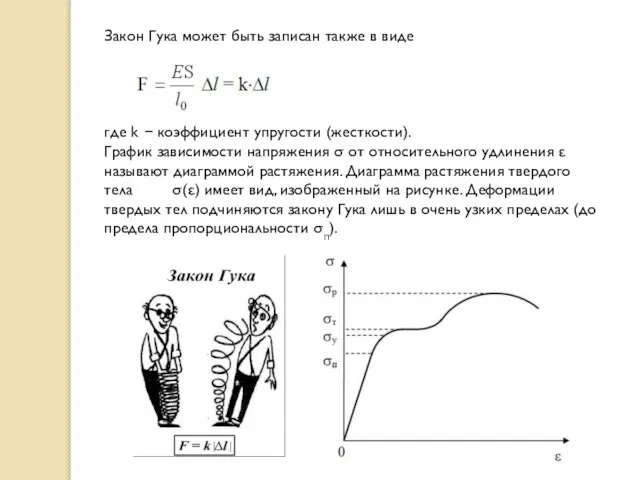
График зависимости напряжения  от относительного удлинения  называют диаграммой растяжения. Диаграмма растяжения твердого тела () имеет вид, изображенный на рисунке. Деформации твердых тел подчиняются закону Гука лишь в очень узких пределах (до предела пропорциональности п).

При увеличении напряжения зависимость () становится нелинейной, хотя деформация еще упругая вплоть до предела упругости (у) (т.е. остаточные деформации не возникают).
При дальнейшем увеличении напряжений в теле возникают остаточные деформации. Напряжение, при котором остаточная деформация достигает  0,2 %, называется пределом текучести (т). При этом деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций).
Материалы, для которых область текучести значительна, называются вязкими, а для которых область текучести практически отсутствует  хрупкими.
Дальнейший рост напряжения приводит к разрушению тела. Максимальное напряжение, предшествующее разрушению тела, называется пределом прочности (р).
Одно и то же твердое тело может при сильном кратковременном воздействии вести себя как хрупкое, а при слабом длительном – как вязкое.

Задача 1.
Определить жесткость пружины, если под действием силы 80 Н она удлинилась на 5 см.
Решение.
Задача 2.
Две пружины, скрепленные одними концами, растягиваются за свободные концы руками. Пружина с жесткостью 100 Н/м удлинилась на 5 см. Какова жесткость второй пружины, если она удлинилась на 3 см.
Решение.
Надо иметь в виду, что по третьему закону Ньютона на пружины действуют равные силы. Запишем равенство их абсолютных величин, а затем преобразуем его.

Силы трения
Силы трения возникают как при относительном
перемещении соприкасающихся тел или их частей,
так и при их относительном покое.
Трение называют внешним, если оно действует между различными соприкасающимися телами (например, трение между бруском и наклонной плоскостью, на которой он лежит или с которой соскальзывает).
Если же трение проявляется между различными частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых непрерывно меняются от слоя к слою, то трение называют внутренним.
Трение между поверхностями двух соприкасающихся твердых тел при отсутствии между ними жидкой или газообразной прослойки (смазки) называют сухим.
Трение между поверхностью твердого тела и окружающей его жидкой или газообразной средой, в которой оно движется, а также трение между различными слоями такой среды, называют вязким.

В случае сухого трения силы трения существуют как при относительном движении соприкасающихся тел, так и при их относительном покое (силы трения покоя), а жидкое трение возможно лишь при относительном движении тел или частей тела. Применительно к сухому трению, когда соприкасающиеся тела движутся друг относительно друга, различают трение скольжения и трение качения.
С трением мы сталкиваемся на каждом шагу, но без трения мы не сделали бы и шага. Невозможно представить себе мир без сил трения. В отсутствие трения многие кратковременные движения продолжались бы бесконечно. Земля сотрясалась бы от непрерывных землетрясений, так как тектонические плиты постоянно сталкивались между собой. Все ледники сразу же скатились бы с гор, а по поверхности земли носилась бы пыль от прошлогоднего ветра…
С другой стороны, трение между деталями машин приводит к их износу и дополнительным расходам. Приблизительные оценки показывают, что научные исследования в трибологии – науки о трении – могли бы сберечь около от 2 до 10% национального валового продукта.

Два самых главных изобретения человека - колесо и добывание огня - связаны с силой трения. Изобретение колеса позволило значительно уменьшить силу, препятствующую движению, а добывание огня поставило силу трения на службу человеку. Однако до сих пор учёные далеки от полного понимания физических основ силы трения. И вовсе не потому, что людей с некоторых пор перестало интересовать это явление.
Первая формулировка законов трения принадлежит великому Леонардо да Винчи, который утверждал, что сила трения, возникающая при контакте тела с поверхностью другого тела, пропорциональна силе прижатия, направлена против направления движения и не зависит от площади контакта.
Этот закон был заново открыт через 180 лет Г. Амонтоном, а затем уточнён в работах Ш. Кулона (1781). Амонтон и Кулон ввели понятие коэффициента трения как отношения силы трения к нагрузке, придав ему значение физической константы, полностью определяющей силу трения для любой пары контактирующих материалов.
где постоянную  называют коэффициентом трения (соответственно покоя или скольжения). Она зависит от свойств соприкасающихся поверхностей.

Леонардо да Винчи
Г.Амонтон
Ш.О. Кулон
Не подмажешь, не поедешь.
Пошло дело как по маслу.
Что кругло – легко катится.
Из навощенной нити сеть не сплетешь.
Угря в руках не удержишь.
Народная мудрость…

Итак, трение – один из видов взаимодействия тел. Оно возникает при соприкосновении двух тел. Трение, как и все другие виды взаимодействия, подчиняется третьему закону Ньютона: если на одно из тел действует сила трения, то такая же по модулю, но направленная в противоположную сторону сила действует и на второе тело.
Силы трения, как и упругие силы, имеют электромагнитную природу. Они возникают вследствие взаимодействия между атомами и молекулами соприкасающихся тел.
Трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону

Сила трения покоя не может превышать некоторого максимального значения Fmax. Если внешняя сила больше Fmax, то возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения
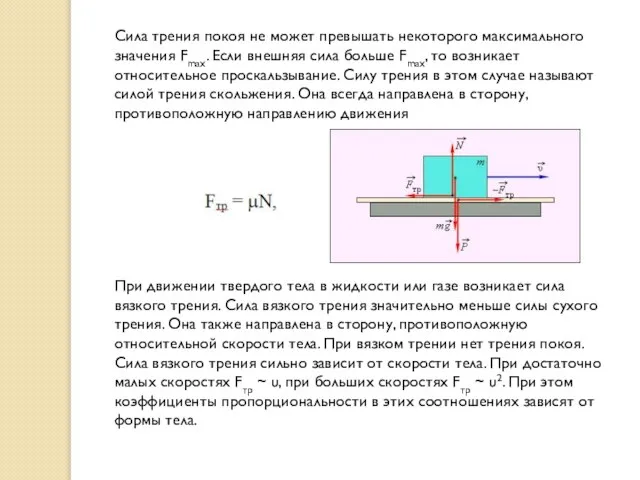
При движении твердого тела в жидкости или газе возникает силa вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя.
Сила вязкого трения сильно зависит от скорости тела. При достаточно малых скоростях Fтр ~ υ, при больших скоростях Fтр ~ υ2. При этом коэффициенты пропорциональности в этих соотношениях зависят от формы тела.

Всегда ли справедлив классический закон трения?
Уже в XIX веке стало ясно, что закон Амонтона-Кулона не всегда правильно описывает силу трения, а коэффициенты трения отнюдь не являются универсальными характеристиками. Прежде всего, было отмечено, что коэффициенты трения зависят не только от того, какие материалы контактируют, но и от того, насколько гладко обработаны контактирующие поверхности. Выяснилось, например, что коэффициенты трения в вакууме всегда больше, чем при нормальных условиях.
Комментируя эти расхождения, лауреат Нобелевской премии по физике Р.Фейнман в своих лекциях писал:
- …Таблицы, в которых перечислены коэффициенты трения "стали по стали", "меди по меди" и прочее, всё это сплошное надувательство, ибо в них этими мелочами пренебрегают, а ведь они-то и определяют значение μ . Трение "меди о медь" и т.д. – это на самом деле трение "о загрязнения, приставшие к меди".

Можно, конечно, пойти по другому пути и, изучая трение «меди по меди», измерять силы при движении идеально отполированных и дегазированных поверхностей в вакууме. Но тогда два таких куска меди просто слипнутся, и коэффициент трения покоя начнёт расти со временем, прошедшем с начала контакта поверхностей. По тем же причинам коэффициент трения скольжения будет зависеть от скорости (расти с её уменьшением). Значит, точно определить силу трения для чистых металлов тоже невозможно.
Тем не менее, для сухих стандартных поверхностей классический закон трения почти точен, хотя причина такого вида закона до самого последнего времени оставалась непонятной. Ведь теоретически оценить коэффициент трения между двумя поверхностями никто так и не смог.
Сложность изучения трения заключается в том, что место, где этот процесс происходит, скрыт от исследователя со всех сторон. Несмотря на это, учёные уже давно пришли к заключению, что сила трения связана с тем, что на микроскопическом уровне (т.е., если посмотреть в микроскоп) соприкасающиеся поверхности очень шероховатые даже, если они были отполированы.

Прежде думали, что механизм трения несложен: поверхность покрыта неровностями, и трение есть результат следующих друг за другом циклов «подъём-спуск» скользящих частей. Но это неправильно, ведь тогда не было бы потерь энергии, а при трении расходуется энергия.
Более близкой к действительности можно считать следующую модель трения. При скольжении трущихся поверхностей их микронеровности соприкасаются, и в точках соприкосновения противостоящие друг другу атомы притягиваются друг к другу, как бы, "сцепляются". При дальнейшем относительном движении тел эти сцепки рвутся, и возникают колебания атомов, подобные тем, какие происходят при отпускании растянутой пружины. Со временем эти колебания затухают, а их энергия превращается в тепло, растекающееся по обоим телам. В случае скольжения мягких тел возможно также разрушение микронеровностей, так называемое "пропахивание", в этом случае механическая энергия расходуется на разрушение межмолекулярных или межатомных связей.

Таким образом, если мы хотим изучать трение нам надо ухитриться двигать песчинку, состоящую из несколько атомов вдоль поверхности на очень маленьком расстоянии от неё, измеряя при этом силы, действующие на эту песчинку со стороны поверхности. Это стало возможным только после изобретения атомно-силовой микроскопии. Создание атомно-силового микроскопа (АСМ), способного чувствовать силы притяжения и отталкивания, возникающие между отдельными атомами, дало возможность, наконец, «пощупать», что такое силы трения, открыв новую область науки о трении – нанотрибологию.
Трение играет большую роль в природе и технике. Во многих случаях силы трения оказываются полезными. Так, автомобиль приводится в движение силами трения, действующими между шинами колес и полотном дороги. Силы трения между поверхностью дороги и подошвами пешеходов способствуют перемещению пешеходов. Силы трения, возникающие между приводным ремнем и шкивами, осуществляют передачу движения от одного маховика к другому. Благодаря трению удерживается забитый в стену гвоздь и т. д.

В некоторых случаях силы трения оказывают вредное действие. Таковы, например, силы трения, возникающие между деталями машин. Они приводят к преждевременному износу машин, и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно меньшим внутренним трением жидкости. Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники и т.д.).

Коэффициент трения скольжения можно найти с помощью наклонной плоскости.
Тело на наклонной плоскости приходит в движение только когда тангенциальная составляющая силы тяжести больше силы трения , т.е. в предельном случае (перед началом скольжения тела):
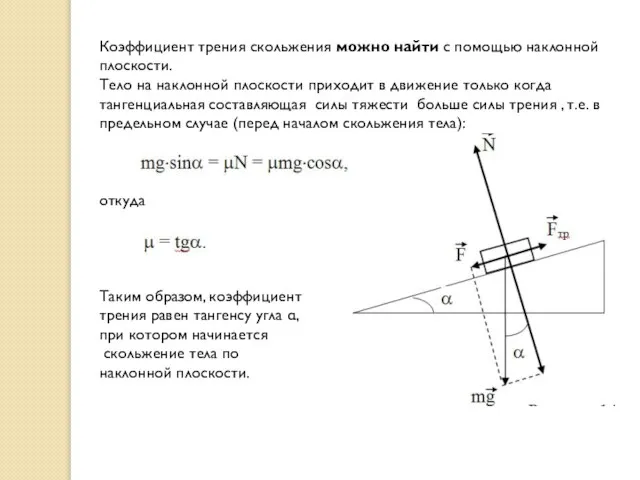
откуда
Таким образом, коэффициент
трения равен тангенсу угла ,
при котором начинается
скольжение тела по
наклонной плоскости.

Задача 1. Тело массой 4,9 кг лежит на горизонтальной плоскости. Какую силу надо приложить к телу в горизонтальном направлении, чтобы сообщить ему ускорение 0,5 м/с2 при коэффициенте трения 0,1?
Решение.
Записываем в векторной форме второй закон Ньютона:
В проекциях на оси:
После подстановок:

Задача 2.
На горизонтальном столе лежит деревянный брусок массой 500 г, который приводится в движение грузом массой 300 г, подвешенным на вертикальном конце нити, перекинутой через блок, закрепленный на конце стола. Коэффициент трения при движении бруска равен 0,2. С каким ускорением будет двигаться брусок?
Решение.
Проекции сил и соответствующих ускорений на оси:
После подстановок и преобразований имеем:
иилили

Задача 3.
На горизонтальную плоскость поставили тело массой 2 кг и приложили к нему силу F=5 Н, направленную горизонтально. Найти силу трения при коэффициенте трения µ=0,2 и µ=0,4
Решение.
Обратим внимание, что в данной задаче неизвестно, движется тело или нет. Поэтому неизвестно, является ли сила трения силой трения покоя или скольжения. Предположим, что тело движется. Тогда мы имеем место с силой трения скольжения.
Запишем второй закон Ньютона в проекциях на оси:
После простых преобразований получим
(при учете, разумеется, что Fmр = µN )

При µ=0,2 подстановка дает:
При µ=0,4 имеем:
Ускорение отрицательно, следовательно наше предположение о том, что тело будет двигаться, неверно (отрицательная величина указывает на равнозамедленное движение, но по условию задачи изначально тело покоилось, а не двигалось!)
Следовательно, сила трения в действительности является силой трения покоя и её нельзя рассчитывать по формуле
Амонтона-Кулона.
В этом случае :
Ускорение положительно, следовательно наше предположение
о том, что тело будет двигаться, верно, следовательно, сила
трения действительно является силой трения скольжения.
В этом случае: