Презентация на тему Гармонические колебания

Давайте вспомним
Колебания – …
процесс, который частично или полностью повторяется через некоторый промежуток времени.
Например, …

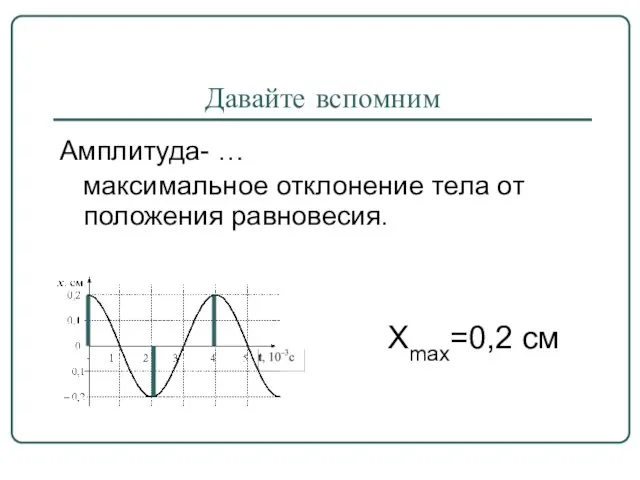
Давайте вспомним
Амплитуда- …
максимальное отклонение тела от положения равновесия.
Хmax=0,2 см

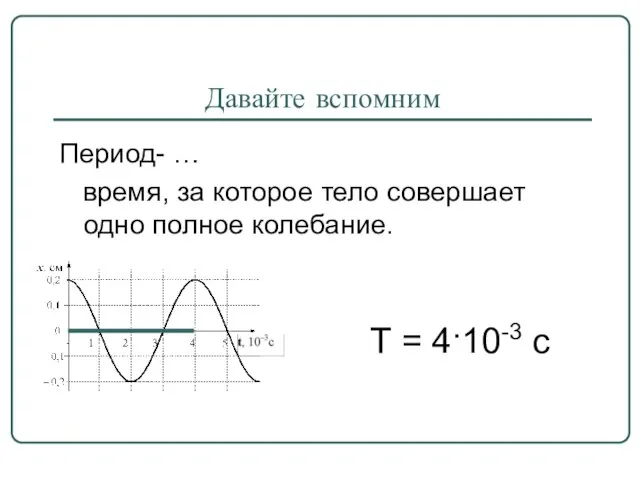
Давайте вспомним
Период- …
время, за которое тело совершает одно полное колебание.
Т = 4·10-3 с

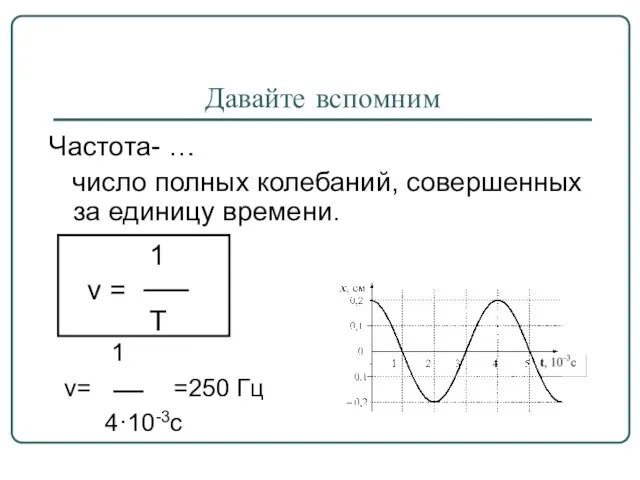
Давайте вспомним
Частота- …
число полных колебаний, совершенных за единицу времени.
1
ν= =250 Гц
4·10-3с

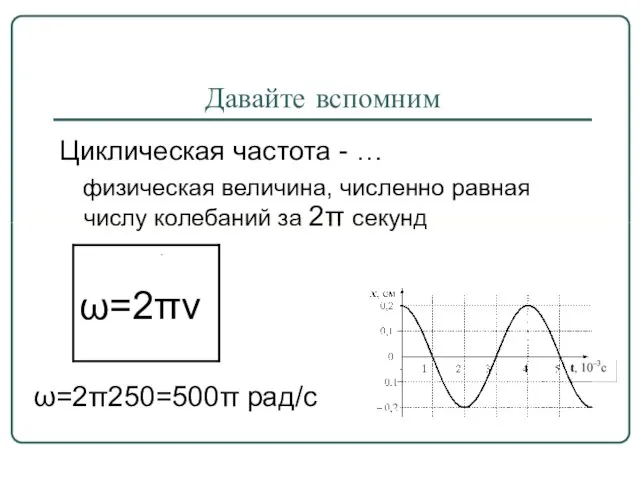
Давайте вспомним
Циклическая частота - …
физическая величина, численно равная числу колебаний за 2π секунд
ω=2π250=500π рад/с

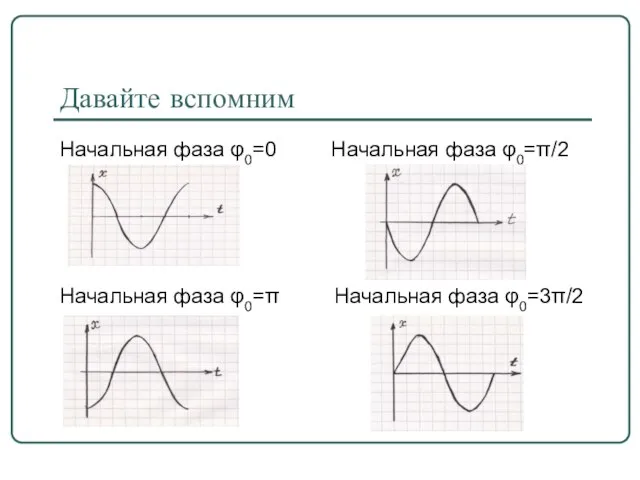
Давайте вспомним
Начальная фаза φ0=0
Начальная фаза φ0=π/2
Начальная фаза φ0=π
Начальная фаза φ0=3π/2

Уравнение гармонических колебаний
Гармонические колебания – это колебания, происходящие по закону синуса или косинуса
φ = ωt + φ0 – фаза колебаний в данный момент времени
ω – циклическая частота
ω=2πν
φ0 – начальная фаза колебаний
Xm – амплитуда колебаний
x = xm cos (ωt + φ0)

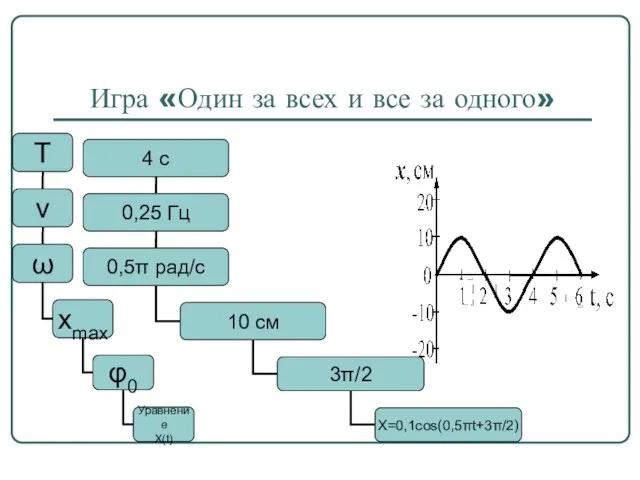
Игра «Один за всех и все за одного»

Уравнение гармонических колебаний
Гармонические колебания – это колебания, происходящие по закону синуса или косинуса
φ = ωt + φ0 – фаза колебаний в данный момент времени
ω – циклическая частота
ω=2πν
φ0 – начальная фаза колебаний
Xm – амплитуда колебаний
x = xm cos (ωt + φ0)

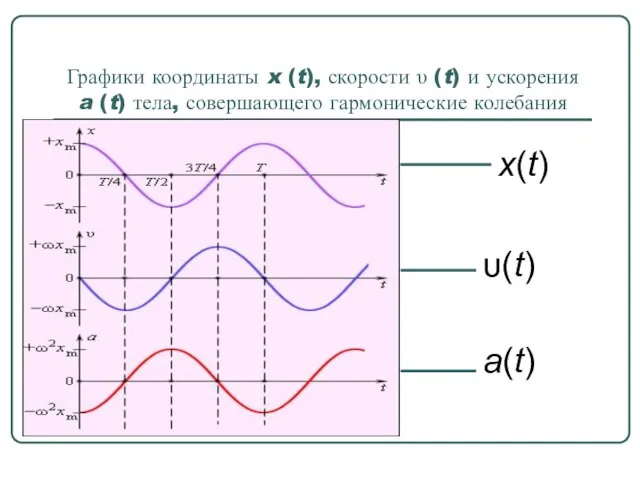
Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания
a(t)
υ(t)
x(t)