Презентация на тему ГИА 2017 Модуль «Геометрия» № 11

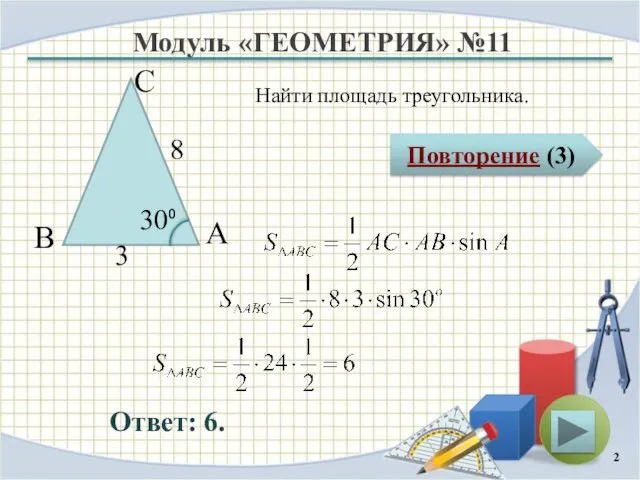
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: 6.
Найти площадь треугольника.
В
С
А
8
3
30⁰

Повторение
Площадь треугольника равна половине произведения двух сторон на синус угла между ними

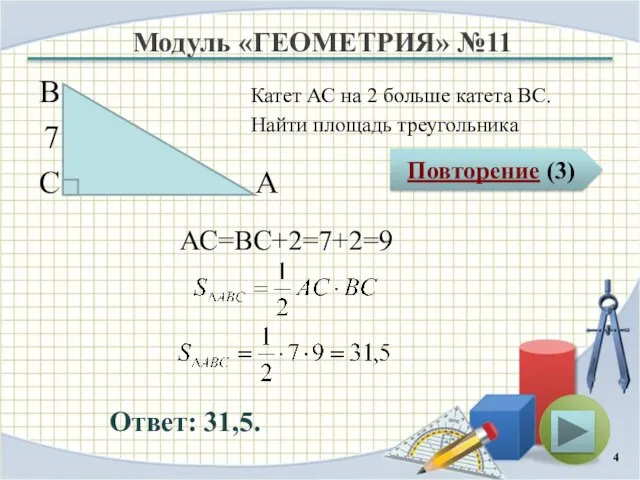
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: 31,5.
Катет АС на 2 больше катета ВС.
Найти площадь треугольника
В
С
А
7
АС=ВС+2=7+2=9

Повторение
Площадь прямоугольного треугольника равна половине произведения катетов

Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: .
Найти площадь треугольника
В
А
С
4

Повторение
Площадь треугольника равна половине произведения двух сторон на синус угла между ними
Сумма квадратов синуса и косинуса одного и того же угла равна единице

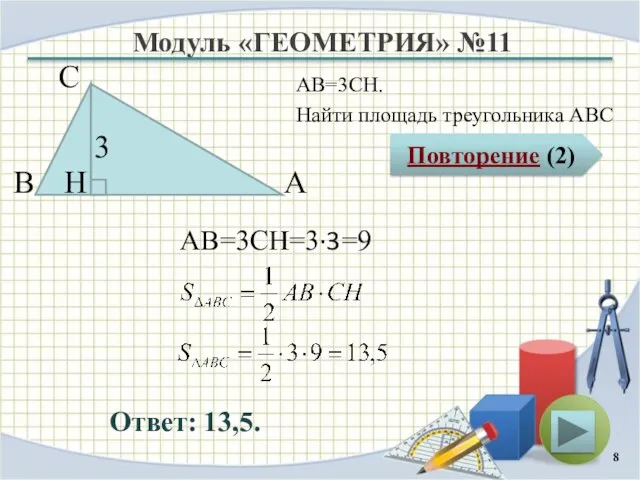
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 13,5.
АВ=3CH.
Найти площадь треугольника АВС
В
С
А
3
H
АВ=3CH=3∙3=9

Повторение
Высота треугольника – это отрезок, проведенный из вершины к противоположной стороне под прямым углом
Площадь треугольника равна половине произведения основания на высоту

Модуль «ГЕОМЕТРИЯ» №11
Повторение (1)
Ответ:1,5 .
P∆ABC =6. Найти S∆ABC
В
С
А
O

Повторение
Если в треугольник вписана окружность, то площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности
Вписанной в треугольник окружностью называется окружность, которая касается всех сторон треугольника

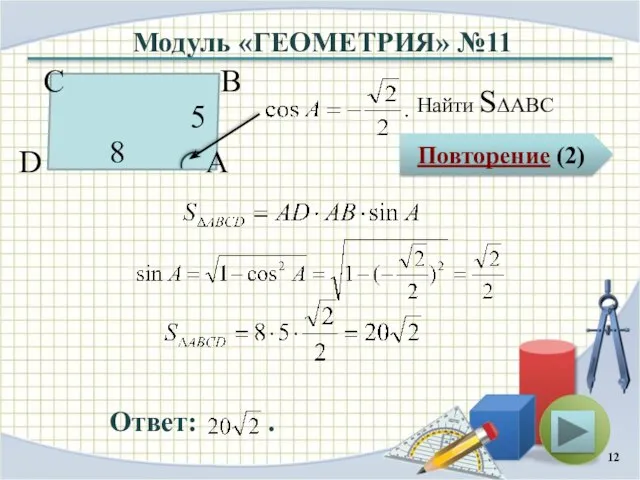
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: .
Найти S∆ABC
В
А
D
С
8
5

Повторение
Площадь параллелограмма равна произведению двух сторон на синус угла между ними
Сумма квадратов синуса и косинуса одного и того же угла равна единице

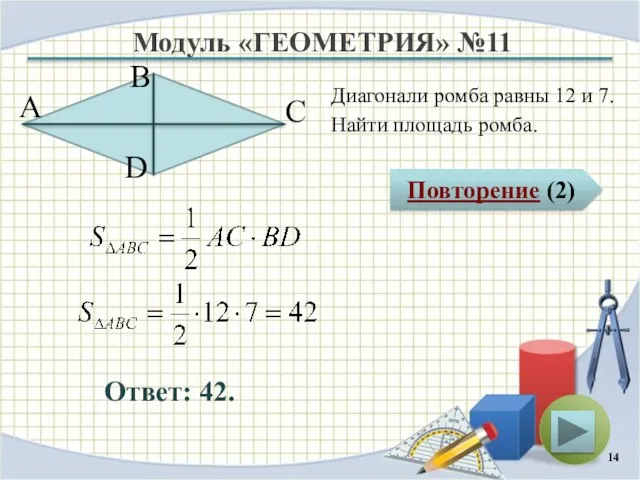
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 42.
Диагонали ромба равны 12 и 7.
Найти площадь ромба.
В
А
D
С

Повторение
Площадь ромба равна половине произведения его диагоналей
Ромб – это параллелограмм с равными сторонами

Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 73,5.
ABCD – трапеция. ВС в 2 раза меньше AD. Найти площадь трапеции
В
А
D
С
14
H
ВС=14:2=7
BC=DH=7

Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Трапеция – это четырехугольник, две стороны которого параллельны

Модуль «ГЕОМЕТРИЯ» №11
Повторение (5)
Ответ: .
АС=10.
Найти площадь прямоугольника
В
А
D
С
60⁰
О
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰
⇒
АВ=5
По теореме Пифагора в ∆АВD

Повторение
Диагонали прямоугольника равны и делятся точкой пересечения пополам
В равнобедренном треугольнике углы при основании равны
Если угол разбит на части, то его градусная мера равна сумме его частей
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению соседних сторон

Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: .
ABCD – равнобедренная трапеция MK=8, боковая сторона равна 5.
Найти площадь трапеции.
В
А
D
С
8
135⁰
H
К
М
⇒
По теореме Пифагора в ∆АВH, где AH=BH=х
∠АВH=90⁰=135⁰-90⁰=45⁰
⇒
∠ВАH= ∠АВC=45⁰
⇒

Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Средняя линия трапеции равна полусумме оснований
Если в прямоугольном треугольнике острый угол равен 45⁰, то и другой острый угол равен 45⁰
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 168.
P∆ABC =98. Найти S∆ABC
В
С
А
25
H
АВ=P∆ABC –2ВС=98–2∙25=48
Т.к. ∆АВС равнобедренный, то АH=HB=48:2=24
По теореме Пифагора в ∆АСH

Повторение
Периметр треугольника – это сумма длин сторон треугольника
Высота в равнобедренном треугольнике, проведенная к основанию является медианой
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 9.
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна медиане, проведенной из того же угла, АВ=6. Найти S∆ABC
В
С
А
H
Если высота треугольника равна медиане, то ∆АВС – равнобедренный с основанием АВ
⇒
∠А=∠В=45⁰
∆HBC прямоугольный и равнобедренный, так как∠В=45⁰
⇒
CH=HВ=AB:2=3

Повторение
Если высота треугольника является и медианой, то такой треугольник равнобедренный
Если прямоугольный треугольник равнобедренный, то его острые углы равны 45⁰
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: .
Найти S∆ABC
В
С
А
6
H
⇒
⇒
Т.к.∆АBC равнобедренный, то AH – медиана
⇒
BC=2BH=
По теореме Пифагора в ∆АВH

Повторение
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе
Высота прямоугольного треугольника, проведенная к основанию, является медианой
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь треугольника равна половине произведения основания на высоту

Модуль «ГЕОМЕТРИЯ» №11
Повторение (4)
Ответ: 90.
Четырехугольник АВСD описан около четырехугольника, радиуса 4,5. Найти S∆ABCD.
В
А
D
С
5
15
4,5
О
Соединим центр окружности с вершинами четырехугольника
Получим треугольники, высоты которых равны радиусу окружности
AB+DC=AD+BC
⇒
S∆AОB +S∆BOC =S∆COD +S∆AOD
SABCD =2(S∆AОB +S∆BOC)
⇒

Повторение
Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны
Если фигура разбита на части, то площадь фигуры равна сумме площадей ее частей
Радиус, проведенный в точку касания перпендикулярен касательной
Площадь треугольника равна половине произведения основания на высоту

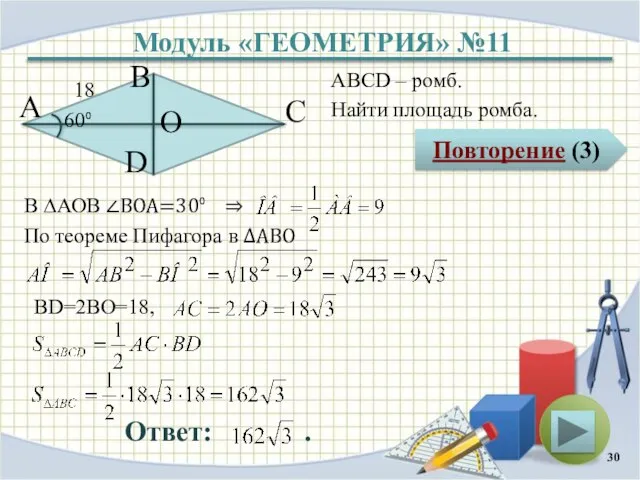
Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: .
ABCD – ромб.
Найти площадь ромба.
В
А
D
С
60⁰
18
O
В ∆АОB ∠ВОА=30⁰
⇒
По теореме Пифагора в ∆АВО
BD=2BO=18,

Повторение
Диагонали ромба перпендикулярны и делят углы ромба пополам
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь ромба равна половине произведения его диагоналей

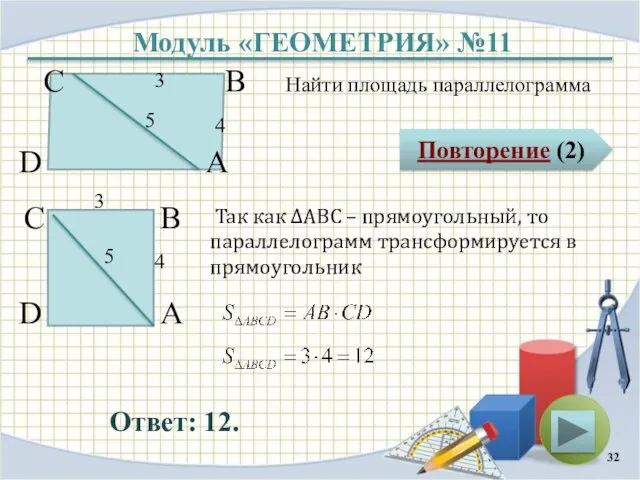
Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 12.
Найти площадь параллелограмма
В
А
D
С
5
4
3
В
А
D
С
5
4
3
Так как ∆АВС – прямоугольный, то параллелограмм трансформируется в прямоугольник

Повторение
Треугольник, в котором стороны равны 3,4,5 называется Пифагоровым (т.е. треугольник является прямоугольным)
Площадь прямоугольника равна произведению его измерений

Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: 192π .
Дуга сектора равна 8π. Найти площадь сектора.
30⁰
O
А
В
Сокр.=360⁰:30⁰∙ 8π=96π
Сокр.=2πr
⇒

Повторение
Длина окружности равна удвоенному произведению числа π на радиус окружности
Площадь кругового сектора
вычисляется по формуле

Модуль «ГЕОМЕТРИЯ» №11
Повторение (2)
Ответ: .
Найти площадь кольца
3
5
⇒

Повторение
Площадь круга равна произведению числа π на квадрат радиуса круга
Если фигура разделена на части, то его площадь равна сумме площадей его частей

Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: .
Найти площадь круга, вписанного в равносторонний треугольник
В
С
А
⇒
⇒

Повторение
Сторона правильного треугольника, в который вписана окружность, равна
Радиусы вписанной и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна произведению числа π на квадрат радиуса круга

Модуль «ГЕОМЕТРИЯ» №11
Повторение (3)
Ответ: .
Найти площадь круга, вписанного в квадрат со стороной 18.
18
⇒
⇒

Повторение
Сторона правильного четырехугольника, в который вписана окружность, равна
Радиусы вписанной и описанной окружности около правильного многоугольника связаны
формулой
Площадь круга равна произведению числа π на квадрат радиуса круга