Презентация на тему График с точкой разрыва

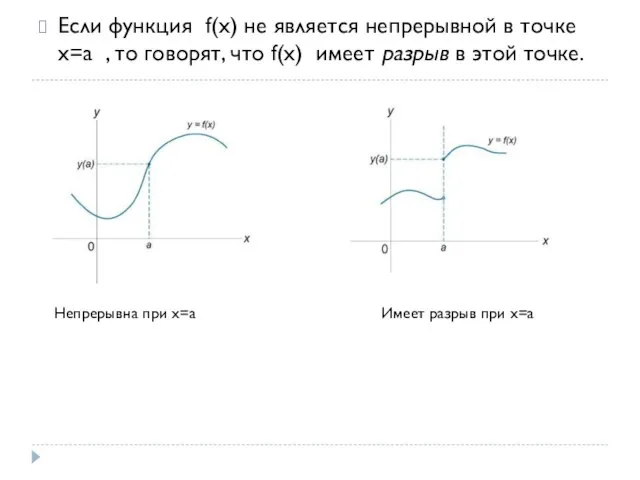
Если функция f(x) не является непрерывной в точке x=a , то говорят, что f(x) имеет разрыв в этой точке.
Непрерывна при x=a
Имеет разрыв при x=a

Определение: функция непрерывна в точке k , если предел функции в данной точке равен значению функции в этой точке:
Определение детализируется в следующих условиях:
1) Функция должна быть определена в точке k, то есть должно существовать значение f(k).
2) Должен существовать общий предел функции . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов: .
3) Предел функции в данной точке должен быть равен значению функции в этой точке:

Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
x0
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Данные точки в свою очередь подразделяются на две большие группы: разрывы первого рода и разрывы второго рода.

Пример. Функция f(x) =– имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
1
X
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

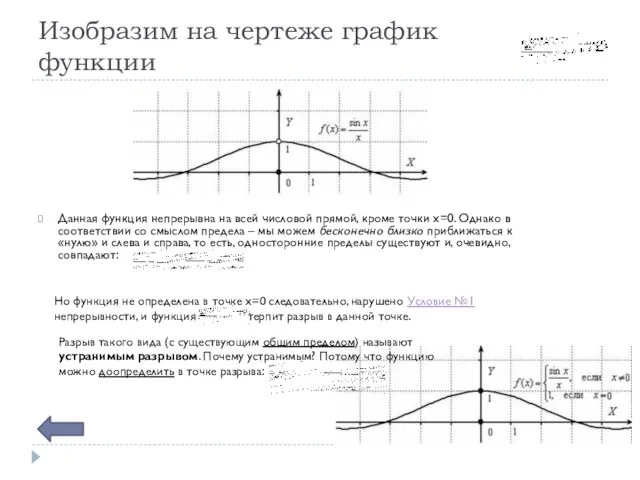
Изобразим на чертеже график функции
Данная функция непрерывна на всей числовой прямой, кроме точки x=0. Однако в соответствии со смыслом предела – мы можем бесконечно близко приближаться к «нулю» и слева и справа, то есть, односторонние пределы существуют и, очевидно, совпадают:
Но функция не определена в точке x=0 следовательно, нарушено Условие №1 непрерывности, и функция терпит разрыв в данной точке.
Разрыв такого вида (с существующим общим пределом) называют устранимым разрывом. Почему устранимым? Потому что функцию можно доопределить в точке разрыва:

Пример.
Найти точки разрыва функции
Решение.
Функция определена и непрерывна при всех x , за исключением точки , где существует разрыв. Исследуем точку разрыва.
Так как значения односторонних пределов конечны, то, следовательно, в точке существует разрыв первого рода. График функции схематически показан на рисунке