Презентация на тему Кинематика Относительность движения

Относительные величины
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.

Пример
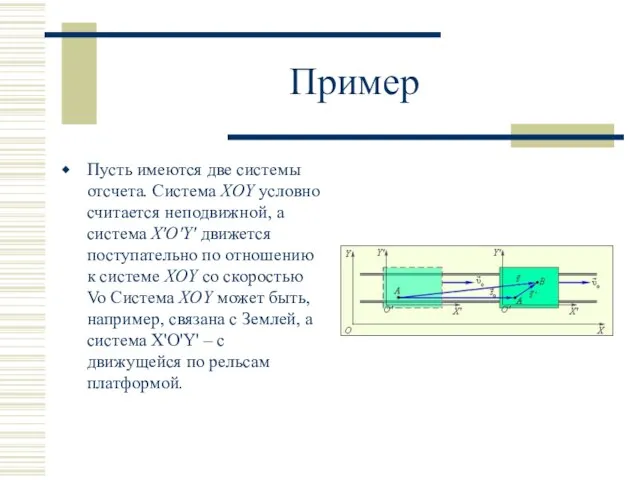
Пусть имеются две системы отсчета. Система XOY условно считается неподвижной, а система X'O'Y' движется поступательно по отношению к системе XOY со скоростью Vo Система XOY может быть, например, связана с Землей, а система X'O'Y' – с движущейся по рельсам платформой.

Перемещение
Пусть человек перешел по платформе за некоторое время из точки A в точку B. Тогда его перемещение относительно платформы соответствует вектору S’, а перемещение платформы относительно Земли соответствует вектору So. Перемещение человека относительно Земли будет соответствовать вектору представляющему собой сумму векторов S’ и So.

Поступательное движение
В случае, когда одна из систем отсчета движется относительно другой поступательно с постоянной скоростью это выражение принимает вид:
S=Vo*Δt+S’

Вектор скорости
Если рассмотреть перемещение за малый промежуток времени ∆t, то, разделив обе части этого уравнения на ∆t и затем перейдя к пределу при ∆t стремящемся к нулю, получим:
V=Vo+V’
где V – скорость тела в неподвижной с/о XOY, V’ – скорость тела в подвижной с/о X'O'Y'.

Абсолютная, относительная и переносная скорости
Обычно скорости V, V’ и Vo называют абсолютной, относительной и переносной скоростями соответственно.