Содержание
- 2. Цели урока: Повторить определение арифметического квадратного корня. Ввести и доказать теорему о квадратном корне из произведения.
- 3. Квадратный корень из произведения План урока: Актуализация знаний. Изучение нового материала. Закрепление формулы на примерах. Самостоятельная
- 4. Здравствуйте, ребята! Повторим : 2. Что называется арифметическим квадратным корнем из числа 3. При каком значении
- 5. Найдите: 1) 2) 3) 7 или или 7
- 6. Сегодня мы познакомимся с одним из свойств арифметического квадратного корня. Введем и докажем теорему о квадратном
- 7. Рассмотрим арифметический корень Найдите значение выражения: Значит, Итак, корень из произведения двух чисел равен произведению корней
- 8. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Если то Теорема
- 9. Квадратный корень из произведения Доказательство: значит, - имеют смысл. 4. Вывод: (т.к. произведение двух неотрицательных чисел
- 10. Мы рассмотрели доказательство теоремы об извлечении квадратного корня из произведения. Перейдём к практической работе. Сейчас я
- 11. Вычислите значение квадратного корня, используя теорему о корне из произведения: Решаем примеры:
- 12. Решаем примеры: 2. Найдите значение выражения:
- 13. Быстрый счёт А я догадался, как можно использовать эту формулу для быстрых вычислений. Смотри и учись.
- 14. Вариант 1 Вариант 2 Предлагаю вам примеры для самостоятельного решения:
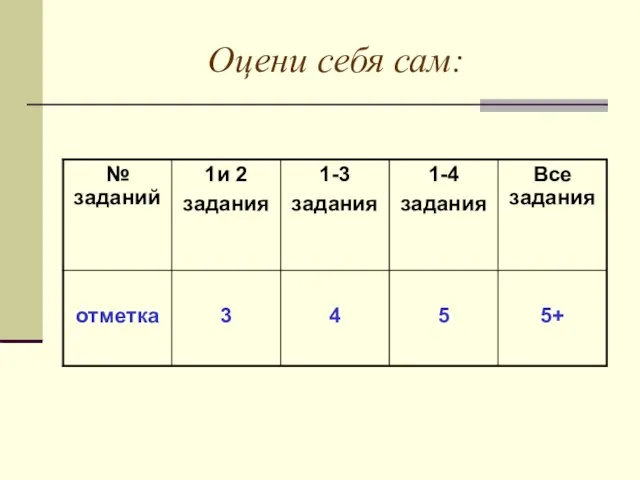
- 15. Оцени себя сам:
- 16. Подведем итоги С какой теоремой мы сегодня познакомились? Сформулируйте правило извлечения квадратного корня из произведения? Когда
- 17. Задание на дом: № 359(а,б), 361(а,б), 363(а,б), 365(а,в).
- 19. Скачать презентацию















 Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит
Ты, человек, любя природу,Хоть иногда её жалей:В увеселительных походахНе растопчи её полей.В вокзальной сутолоке векаТы оценит NXP semiconductors, Москва. Краткий обзор
NXP semiconductors, Москва. Краткий обзор Однофазный TIG-инвертор
Однофазный TIG-инвертор Індекси цін у будівництві
Індекси цін у будівництві Банки и банковская система РФ. Тест
Банки и банковская система РФ. Тест Прикладной Тайм-менеджмент для программистов
Прикладной Тайм-менеджмент для программистов ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет
ГПОУ Горловский автотранспортный техникум. ГОУВПО Донецкий национальный технический университет Кабинет министров
Кабинет министров Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: +
Республиканский научно-исследовательский институт интеллектуальной собственности ул. Б.Якиманка, д. 38, г. Москва, 119049 тел./факс: + Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки
Доброволец на ЧС. Особенности психологической устойчивости личного состава. Способы подготовки Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Перпендикуляр и наклонные
Перпендикуляр и наклонные Однородные члены предложения
Однородные члены предложения Предмет, метод, источники и принципы Трудового права
Предмет, метод, источники и принципы Трудового права Поэты Ставрополья о родном крае и о природе родного края
Поэты Ставрополья о родном крае и о природе родного края Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр
Педагогический совет «Поиск путей совершенствования образовательной среды школы при введении федерального государственного обр Обзор на персонажа
Обзор на персонажа ВКР: Действительный цикл машины МВВ6 - 1 -2
ВКР: Действительный цикл машины МВВ6 - 1 -2 15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом).
15 февраля 1861 года родился швейцарский физик-метролог Шарль Эдуард Гильом (Гийом). Правила наложения жгутов повязок и шин
Правила наложения жгутов повязок и шин Вальдорфская система образования
Вальдорфская система образования Social Ecology Sustainable Development
Social Ecology Sustainable Development  Ваш профессиональный маршрут
Ваш профессиональный маршрут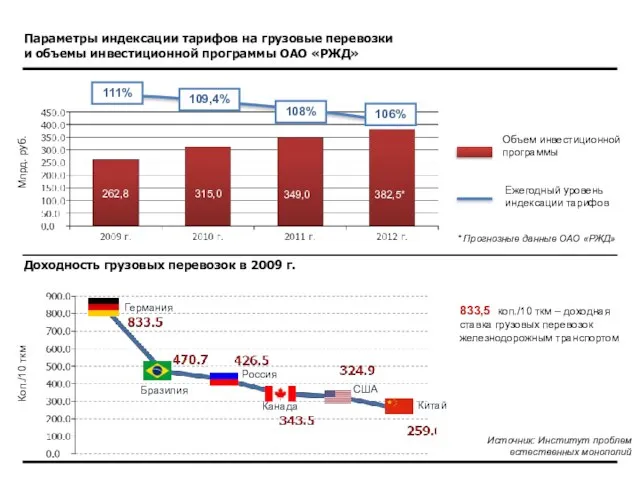 Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД»
Параметры индексации тарифов на грузовые перевозки и объемы инвестиционной программы ОАО «РЖД» Концепция воспитательной системы
Концепция воспитательной системы Технология создания и редактирования изображений в векторном редакторе
Технология создания и редактирования изображений в векторном редакторе Презентация на тему Использования краеведческого материала в образовательном процессе
Презентация на тему Использования краеведческого материала в образовательном процессе