Содержание
- 2. Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой
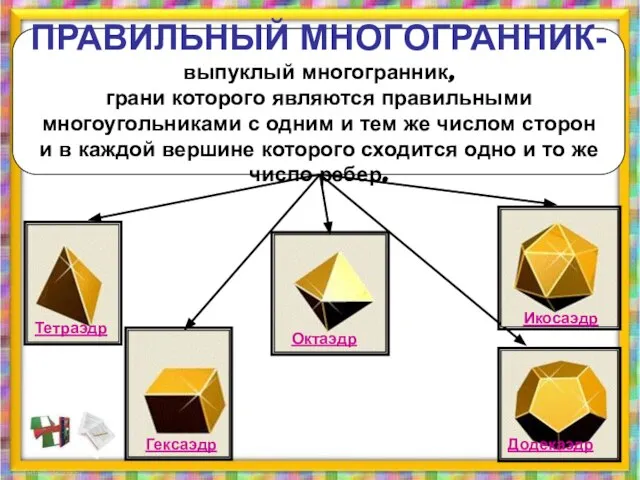
- 3. ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон
- 4. «эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «додека»
- 5. Тетраэдр – представитель правильных выпуклых многогранников. Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой
- 6. Куб или гексаэдр – представитель правильных выпуклых многогранников. Куб имеет шесть квадратных граней, сходящихся в каждой
- 7. Октаэдр – представитель семейства правильных выпуклых многогранников. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине
- 8. Додекаэдр – представитель семейства правильных выпуклых многогранников. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по
- 9. Икосаэдр – представитель семейства правильных выпуклых многогранников. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в
- 10. Платон
- 11. огонь вода воздух земля вселенная тетраэдр икосаэдр октаэдр гексаэдр додекаэдр
- 12. Модель Солнечной системы Кеплера.
- 13. "Космический кубок" И.Кеплера
- 15. Икосаидро-додекаидровая структура Земли.
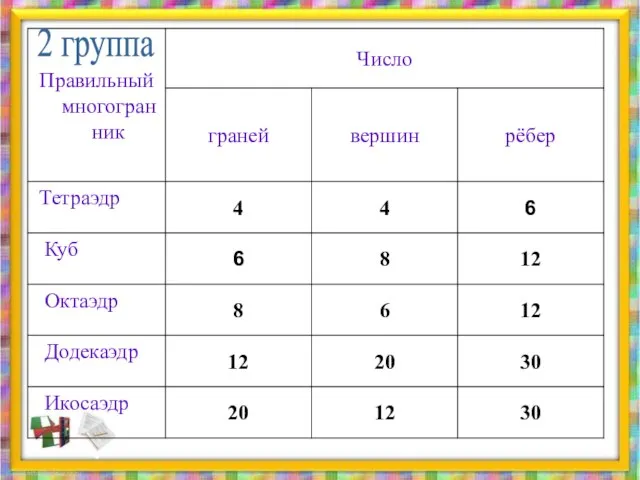
- 16. 1 группа- доказать, что правильных многогранников существует ровно 5. 2 группа- используя модели многогранников, заполнить данную
- 17. Вывод: Существует лишь пять выпуклых правильных многогранников – тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб
- 18. 2 группа
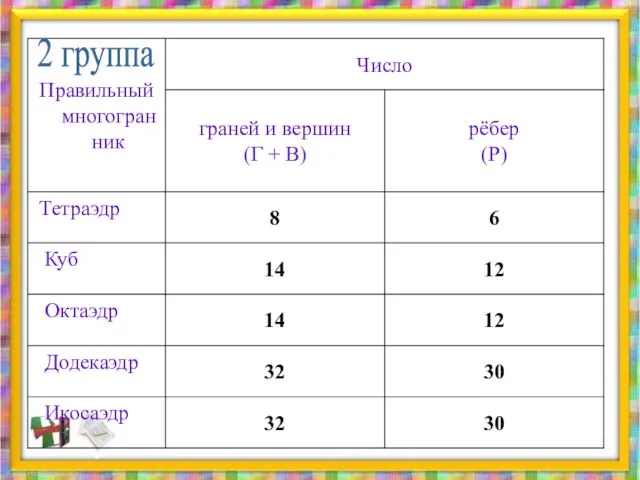
- 19. 2 группа
- 20. Теорема Эйлера Число вершин плюс число граней минус число рёбер равно двум. В + Г –
- 21. Леонард Эйлер (1707 – 1783 гг.) немецкий математик и физик
- 22. 3 группа
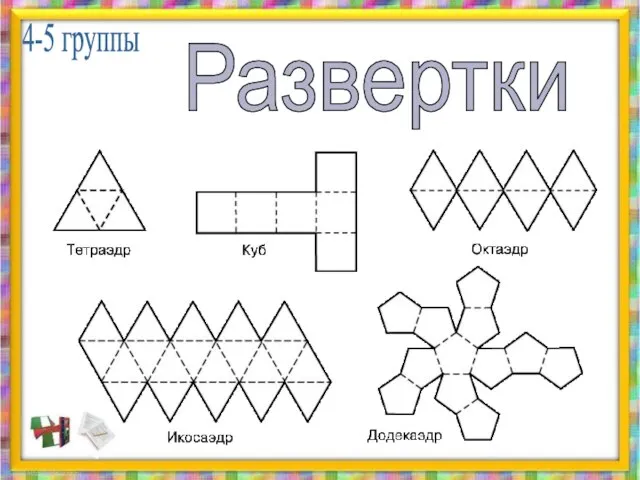
- 23. 4-5 группы Развертки
- 24. Архимедовыми телами называются полуправильные однородные выпуклые многогранники, то есть выпуклые многогранники, все многогранные углы которых равны,
- 25. Архимедовы тела
- 26. Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый
- 27. Малый звездчатый додекаэдр Большой звездчатый додекаэдр Большой икосаэдр Большой додекаэдр
- 28. Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины
- 29. Химия
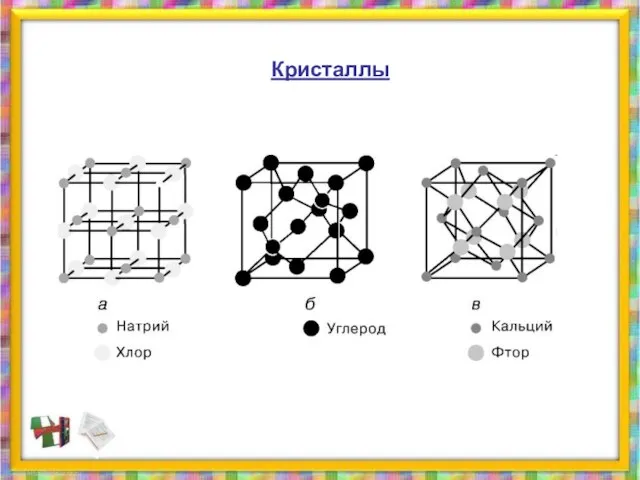
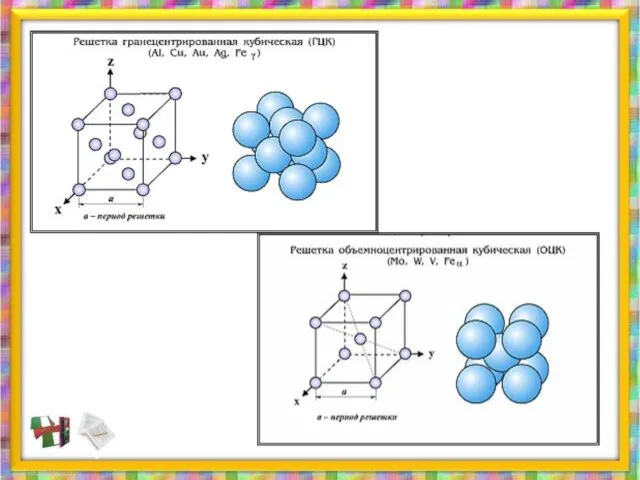
- 30. Кристаллы
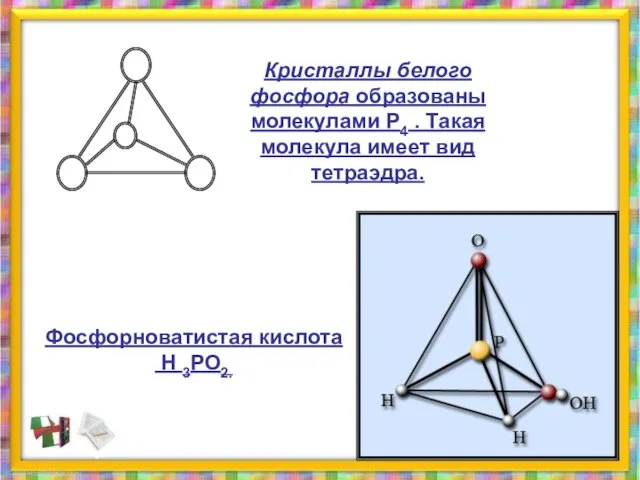
- 31. Кристаллы белого фосфора образованы молекулами Р4 . Такая молекула имеет вид тетраэдра. Фосфорноватистая кислота Н 3РО2.
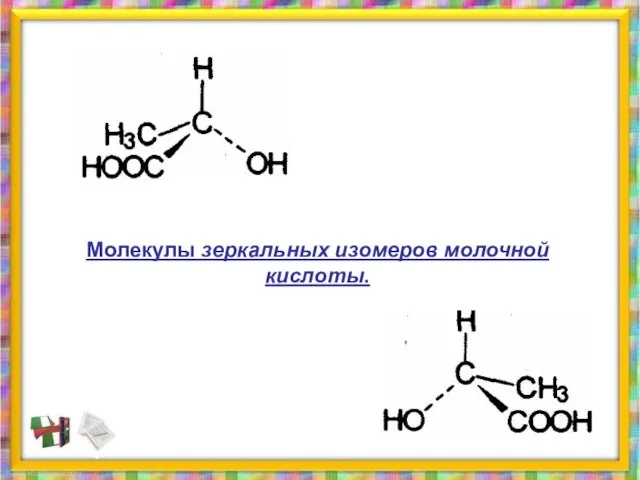
- 32. Молекулы зеркальных изомеров молочной кислоты.
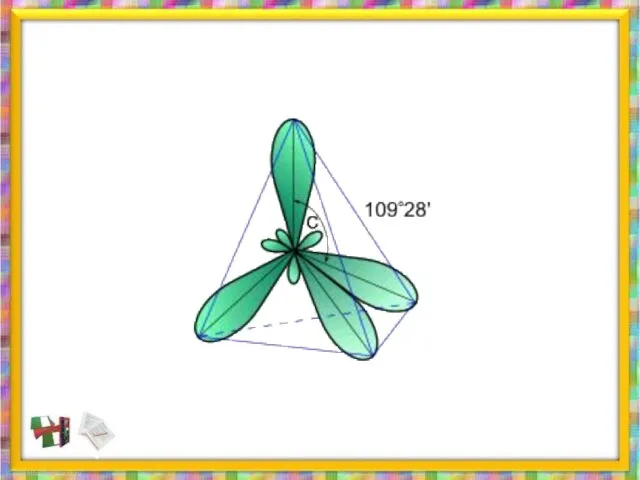
- 34. Строение молекулы метана .
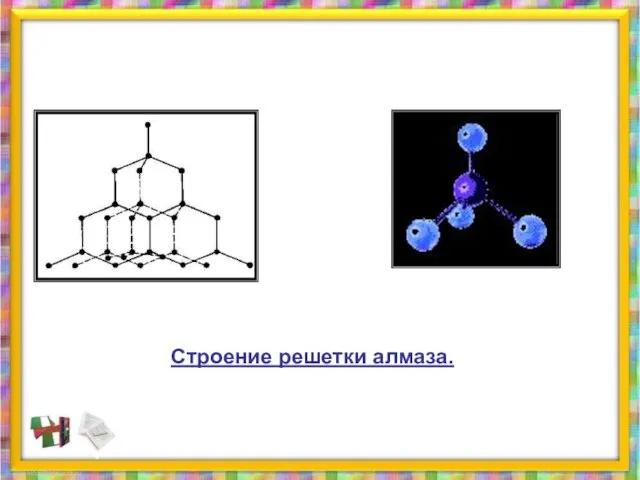
- 35. Строение решетки алмаза.
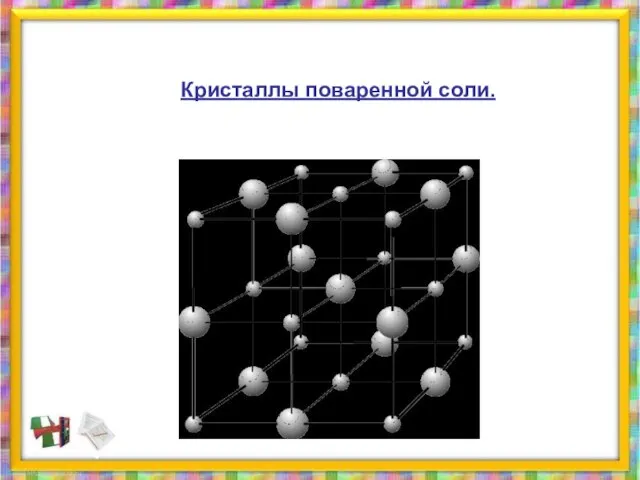
- 36. Кристаллы поваренной соли.
- 38. Биология
- 39. Вирус полиомиелита имеет форму додекаэдра.
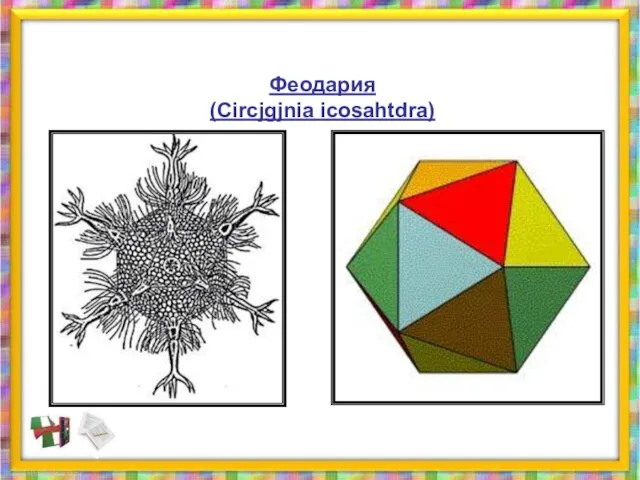
- 40. Феодария (Circjgjnia icosahtdra)
- 41. Искусство «Тайняя вечеря» С.Дали
- 42. ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»
- 44. Украшения
- 45. Правильная форма алмаза.
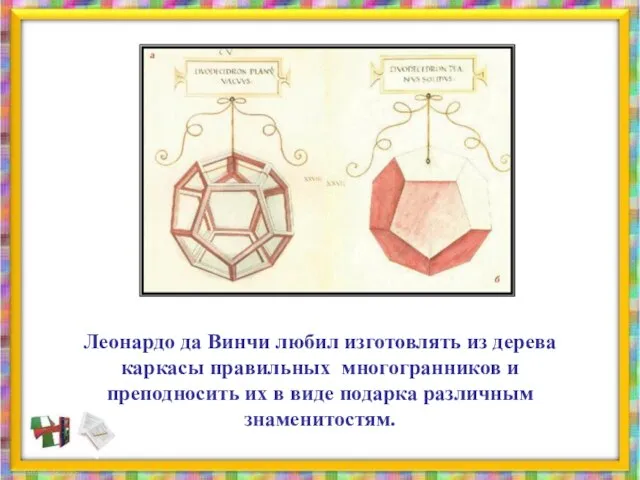
- 46. Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка
- 48. Скачать презентацию
































 Зольные отвалы - источник сырья для производства зольного сухих смесей легких бетонов нового поколения
Зольные отвалы - источник сырья для производства зольного сухих смесей легких бетонов нового поколения Что такое погода (3 класс)
Что такое погода (3 класс) Строение Земли
Строение Земли Путешествие в страну математики
Путешествие в страну математики Докладчик: Дворниченко П.И. – - главный специалист-эксперт по техническому регулированию и промышленной безопасности
Докладчик: Дворниченко П.И. – - главный специалист-эксперт по техническому регулированию и промышленной безопасности
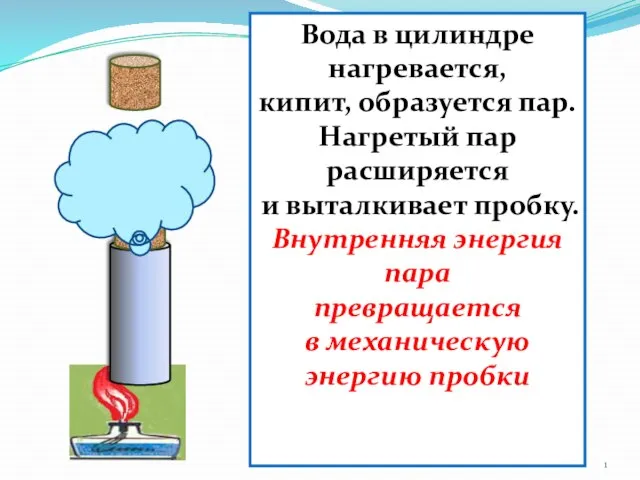 Презентация на тему Тепловые двигатели ДВС
Презентация на тему Тепловые двигатели ДВС  Живопись. Виды, жанры
Живопись. Виды, жанры Рисуем портрет мамы
Рисуем портрет мамы Образовательная технология «Достижения прогнозируемых результатов»
Образовательная технология «Достижения прогнозируемых результатов» Дымовой тест БСП
Дымовой тест БСП Адресаты любовной лирики Лермонтова
Адресаты любовной лирики Лермонтова Confidence intervals
Confidence intervals ПРАКТИКА 6 - копия
ПРАКТИКА 6 - копия Программа повышения конкурентоспособности продукции ОАО Брестское мороженное
Программа повышения конкурентоспособности продукции ОАО Брестское мороженное Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз
Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз «Знакомство с цифрой 8»
«Знакомство с цифрой 8» Наш город – Саранск
Наш город – Саранск Создание рабочих мест
Создание рабочих мест Разработка шагового электропривода на базе одноименно – полюсного индукторного двигателя
Разработка шагового электропривода на базе одноименно – полюсного индукторного двигателя Economic importance of soil
Economic importance of soil Покрытосеменные растения (7 класс)
Покрытосеменные растения (7 класс)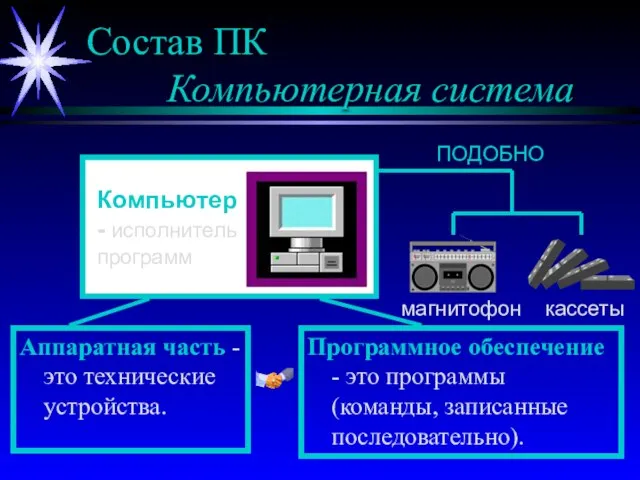 Состав ПК Компьютерная система
Состав ПК Компьютерная система Зрительное ВОСПРИЯТИЕ
Зрительное ВОСПРИЯТИЕ Презентация на тему Как различать причастия и отглагольные прилагательные
Презентация на тему Как различать причастия и отглагольные прилагательные  Интернет в школе- окно в мир… знаний …?
Интернет в школе- окно в мир… знаний …? Компьютерные методы в географических исследованиях
Компьютерные методы в географических исследованиях  Реконструкция набережной Тюмень
Реконструкция набережной Тюмень