Содержание
- 2. Цель урока: обобщить материал по свойствам логарифмов, логарифмической функции; рассмотреть основные методы решения логарифмических уравнений; развивать
- 3. Вспомни и продолжи свойство!
- 4. Вычислите значения выражения
- 5. Вычислить значение выражения
- 6. Определение: Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.
- 9. Решение простейшего логарифмического уравнения основано на применении определения логарифма и решении равносильного уравнения Пример
- 10. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их: если loga f(х)
- 12. Если в уравнении содержатся логарифмы с разными основаниями, то прежде всего следует свести все логарифмы к
- 13. Если в показатели степени содержится логарифм, то обе части уравнения логарифмируют по тому основанию, которое содержится
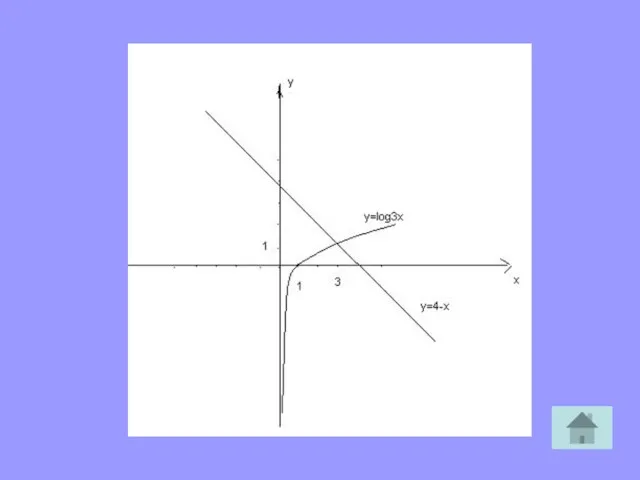
- 14. Для решения ЛУ графическим методом надо построить в одной и той же системе координат графики функций,
- 17. Скачать презентацию






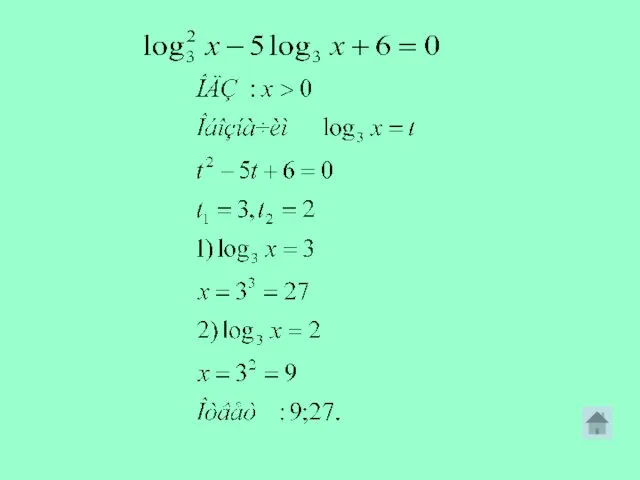






 Как писать статью?
Как писать статью? Презентация на тему АНГЛИЯ ПРИ ТЮДОРАХ
Презентация на тему АНГЛИЯ ПРИ ТЮДОРАХ  Направляется Ф. И. О. _____________________________________________________ _____________________________________________________ Возраст на момент заполнения.
Направляется Ф. И. О. _____________________________________________________ _____________________________________________________ Возраст на момент заполнения. Олимпийское движение
Олимпийское движение VI конференция «Поисковая оптимизация и продвижение сайтов в Интернете» «Динамика уровня цен на ссылки в РУнете по данным CLX.RU за ф
VI конференция «Поисковая оптимизация и продвижение сайтов в Интернете» «Динамика уровня цен на ссылки в РУнете по данным CLX.RU за ф Формирование информационно - коммуникационной компетентности участников образовательного процесса как условие получения соврем
Формирование информационно - коммуникационной компетентности участников образовательного процесса как условие получения соврем По знаменитым местам мира (3 класс)
По знаменитым местам мира (3 класс) Цветовые контрасты 2
Цветовые контрасты 2 Компьютер и здоровье школьников
Компьютер и здоровье школьников Страхование
Страхование Когда сети становятся умными Клаес Ритофт Старший вице-президент АББ
Когда сети становятся умными Клаес Ритофт Старший вице-президент АББ Есть ли жизнь на Марсе?
Есть ли жизнь на Марсе? Information Systems Design
Information Systems Design  Jaguar Cars Ltd
Jaguar Cars Ltd Сущность, структура и динамика международного движения капитала
Сущность, структура и динамика международного движения капитала  Эпитет как выразительно-изобразительное средство в баснях И.А. Крылова
Эпитет как выразительно-изобразительное средство в баснях И.А. Крылова Проект ЦО № 1436.«Плавучая сервисная платформа»
Проект ЦО № 1436.«Плавучая сервисная платформа» Презентация на тему Курская битва
Презентация на тему Курская битва  Трансфертные цены: Трудности перевода 07 ноября 2011 г.
Трансфертные цены: Трудности перевода 07 ноября 2011 г. Не забудь покормить собаку. Ты помнишь, что уже говорил нам об этом? Мы забыли купить хлеба. Мы забыли, что уже купили хлеб. Они помня
Не забудь покормить собаку. Ты помнишь, что уже говорил нам об этом? Мы забыли купить хлеба. Мы забыли, что уже купили хлеб. Они помня Элементы статистики и теории вероятностей в курсе математики основной школы
Элементы статистики и теории вероятностей в курсе математики основной школы Теории возникновения жизни на Земле
Теории возникновения жизни на Земле С праздником САТ и АТП
С праздником САТ и АТП урок 2 презентация к уроку
урок 2 презентация к уроку Мезенская роспись
Мезенская роспись Научно-исследовательская работа студентов (НИРС)
Научно-исследовательская работа студентов (НИРС) Слуховые аппараты и их устройство
Слуховые аппараты и их устройство Unit 11-5. Презентация
Unit 11-5. Презентация