Презентация Сфера и шар.

СОДЕРЖАНИЕ
1.Сказка о возникновении шара.
2.Из истории возникновения.
3.Определение.
4.Общие понятия.
5.Касательная плоскость к сфере.
6.Сечение шара плоскостью.
7.Задача на тему шар.

Сказка о возникновении шара.
Однажды , оставшись один дома, красавец Полукруг долго принаряживался и жеманился перед небольшим в оловянных рамках зеркалом и не мог налюбоваться собою.
«Что людям вздумалось расславлять , будто я хорош?- говорил он. – Лгут люди , я совсем не хорош. Почему девушки провозгласили , что лучшего парня и не было еще никогда и не будет никогда на селе Хатанга?».
Полукруг знал и слышал все, что про него говорили , и был капризным, как красавец . Он мог целый день любоваться собой перед зеркалом , рассматривая себя со всех сторон . И вдруг случилось чудо, когда Полукруг повернулся перед зеркалом вокруг себя, он увидел в зеркале собственное отражение в форме Шара.

ИЗ ИСТОРИИ ВОЗНИКНОВЕНИЯ
Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш.
В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы.
Сфера всегда широко применялось в различных областях науки и техники.

ОПРЕДЕЛЕНИЕ
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.
Тело, ограниченное сферой, называется шаром.

Общие понятия
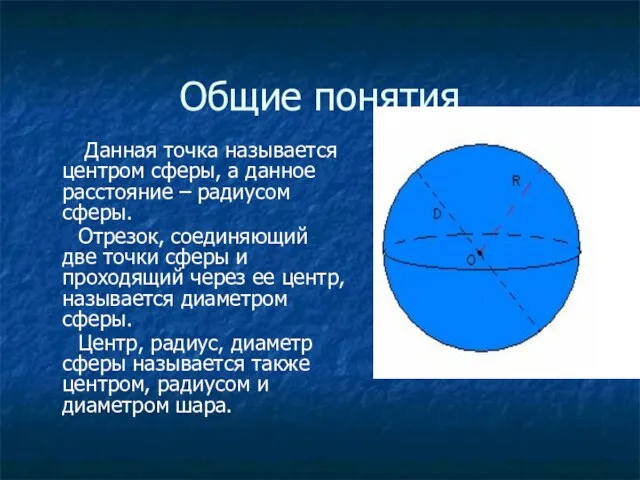
Данная точка называется центром сферы, а данное расстояние – радиусом сферы.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы.
Центр, радиус, диаметр сферы называется также центром, радиусом и диаметром шара.

Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

СЕЧЕНИЕ ШАРА ПЛОСКОСТЬЮ.
Любое сечение шара плоскостью есть круг. Центр этого круга – основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Сечение, проходящее через центр шара, - большой круг. (диаметральное сечение).

ЗАДАЧА НА ТЕМУ ШАР (Д/З).
На поверхности шара даны три точки. Прямолинейные расстояния между ними 6 см, 8 см, 10 см. Радиус шара 13 см. Найдите расстояние от центра до плоскости, проходящей через эти точки.
1. 7см 2. 15см 3. 12см 4. 20см
Инструктаж.
1. Выполним рисунок шара, на его поверхности возьмем три точки.
2. Через три точки проведем плоскость, которая пересечет поверхность шара по окружности, описанной около треугольника со сторонами 6см, 8см, 10см.
3. Радиус описанной окружности найдем по формуле R=abc/s
4. Площадь S найдем по формуле Герона: S=√p(p-a)(p-b)(p-c).
5. По теореме Пифагора находим искомое расстояние:
Х=√ŗ²-R².