Prezentatsia_SARU_lektsia_TAU__1

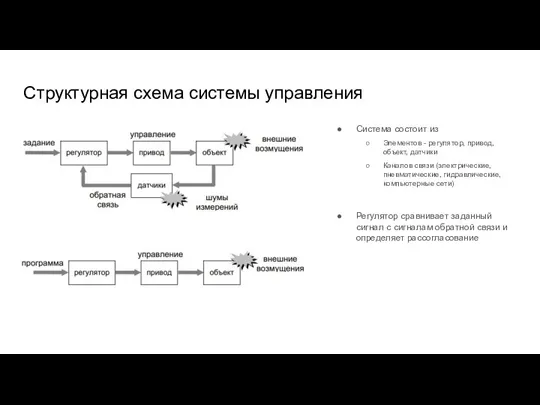
Структурная схема системы управления
Система состоит из
Элементов - регулятор, привод, объект, датчики
Каналов связи (электрические, пневматические, гидравлические, компьютерные сети)
Регулятор сравнивает заданный сигнал с сигналам обратной связи и определяет рассогласование

Задачи управления
Автоматические системы управления применяются для решения трех типов задач:
стабилизация, то есть поддержание заданного режима работы, который не меняется длительное время (задающий сигнал – постоянная, часто нуль)
программное управление – управление по заранее известной программе (задающий сигнал меняется, но заранее известен)
слежение за неизвестным задающим сигналом

Классификация систем управления
По количеству входов и выходов:
одномерные системы (имеющие один вход и один выход)
многомерные системы (имеющие несколько входов и/или выходов)
По характеру сигналов:
непрерывные (все сигналы - функции непрерывного времени, определенные на некотором интервале)
дискретные (используются дискретные сигналы (последовательности чисел), определенные только в отдельные моменты времени
непрерывно-дискретные
Стационарные системы - это системы, в которых все параметры остаются постоянными
Нестационарные системы - это системы, параметры объекта или регулятора изменяются со временем
Детерминированные системы - системы, в которых все параметры объекта (как и внешние воздействия) заданы точно
Стохастические системы - системы, в которых действуют случайные возмущения или параметры объекта могут изменяться случайным образом

Связь входа и выхода
Входы - это возможные воздействия на объект.
Выходы - это сигналы, которые можно измерить.
Правило преобразования входа x в выход y называется оператором U.
Операторная форма записи: y = U[x]
Оператор интегрирования
Оператор дифференцирования
Сокращенная форма записи оператора (p -оператор)
y(t) = p x(t)
Например оператор дифференцирования
p x(t) = dx(t) / dt
Операторы бывают: линейные и нелнейные
Свойства линейных операторов:
умножение на константу: U[a*x] = a * U[x]
принцип суперпозиции: U[x1+x2] = U[x1] + U[x2]
Все реальные системы – нелинейные, поэтому проводят линеаразацию нелинейной модели объекта, т.е. строят приближенную линейную модель.

Линеаризация нелинейной системы
Пример.
Бак с водой. В нижней части просверлено отверстие, через которое вытекает вода.
S - площадь сечения бака
S0 – площадь сечения отверстия
Нужно построить модель, которая связывает уровень воды в баке h (в метрах) и расход вытекающей воды q (в м3/с)
Закон Бернулли: ρ * g * h = ρ * v2 / 2
Скорость: v = sqrt(2 * g * h)
Расход q = S0 * v
Получаем модель
q = a * sqrt(h),
где a = S0 * sqrt(2 * g).
Это статическая модель, потому что она не содержит производных, характеризующих изменение сигналов во времени. Статическая модель описывает установившееся состояние (статический режим), т.е. когда в баке поддерживается постоянны уровень воды и потока вытекающей воды тоже постоянный.
В реальности полученная модель – нелинейная, потому что содержит sqrt(h). Линеаризовать модель – значит приближенно заменить линейным уравнением вида
q = k * h
где k – коэффициент, которые выбирается в зависимости от условий.

… продолжение примера

Модели линейных объектов
Модель объекта, составленная на основании физических законов, чаще всего представляется системой дифференциальных уравнений 1-го и 2-го порядка.
Уравнение «вход-выход» показывает зависимость выходного параметра (сигнал) от входного (воздействия).
Порядок модели определяется порядком дифференциального уравнения.
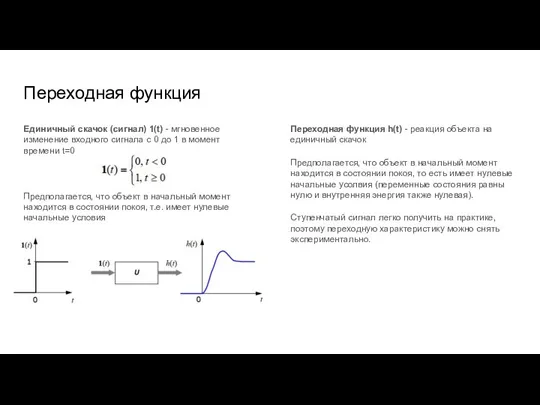
Чтобы легче исследовать модель объекта, желательно привести ее к стандартному виду, для которого уже есть готовые решения. Таким «стандартом» в теории автоматического управления считается система дифференциальных уравнения первого порядка (нормальная форма Коши)

Переходная функция
Единичный скачок (сигнал) 1(t) - мгновенное изменение входного сигнала с 0 до 1 в момент времени t=0
Предполагается, что объект в начальный момент находится в состоянии покоя, т.е. имеет нулевые начальные условия
Переходная функция h(t) - реакция объекта на единичный скачок
Предполагается, что объект в начальный момент находится в состоянии покоя, то есть имеет нулевые начальные усолвия (переменные состояния равны нулю и внутренняя энергия также нулевая).
Ступенчатый сигнал легко получить на практике, поэтому переходную характеристику можно снять экспериментально.

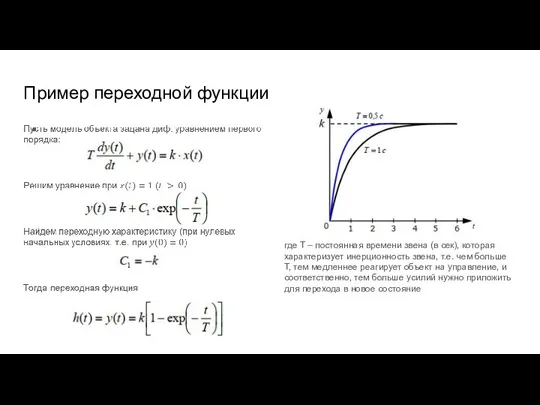
Пример переходной функции
где Т – постоянная времени звена (в сек), которая характеризует инерционность звена, т.е. чем больше Т, тем медленнее реагирует объект на управление, и соответственно, тем больше усилий нужно приложить для перехода в новое состояние

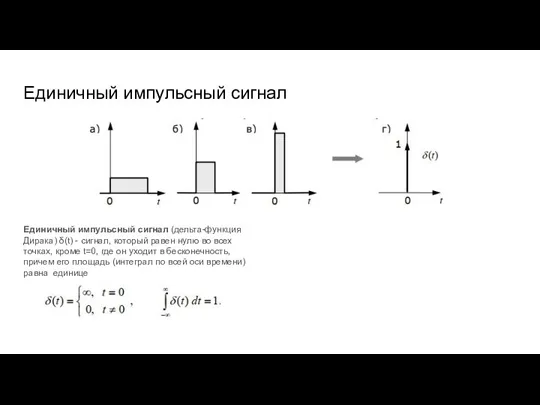
Единичный импульсный сигнал
Единичный импульсный сигнал (дельта-функция Дирака) δ(t) - сигнал, который равен нулю во всех точках, кроме t=0, где он уходит в бесконечность, причем его площадь (интеграл по всей оси времени) равна единице

Импульсная характеристика (весовая функция)
Импульсная характеристика w(t) - реакция объекта на единичный импульсный сигнал
Импульсная характеристика (как и переходная) определяется при нулевых начальных условиях, т.е. объект должен находится в состоянии покоя
Импульсная характеристика дает неполную информацию об объекте, так как не учитывает ненулевые начальные условия
В отличие от ступенчатого сигнала, мгновенный импульс бесконечной величины невозможно получить на реальном устройстве, поэтому снять импульсную характеристику системы не получится

Импульсная характеристика (весовая функция)
Пусть ширина прямоугольного импульса равна ε, а высота равна 1/ε, то такой импульс можно представить в виде разности двух ступенчатых сигналов
Так как для линейных систем справедлив принцип суперпозиции
При ε → 0 импульсная хар-ка равна производной от переходной функции
Переходная функция - это интеграл от импульсной хар-ки в интервале от 0 до t

Пример. Импульсная характеристика
Ранее рассмотренная переходная функция для модели, заданной диф. уравнением 1 порядка
Дифференцируя переходную хар-ку звена 1 порядка, получаем импульсную хар-ку

Передаточная функция
Пусть модель задана линейным диф. уравнением 2-го порядка
Введем оператор дифференцирования
С учетом оператора дифференцирования модель объекта можно переписать:

Правильная передаточная функция - если степень ее числителя не больше, чем степень знаменателя.
Строго правильная передаточная функция - если степень ее числителя меньше, чем степень знаменателя.
Неправильная передаточная функция - если степень ее числителя больше, чем степень знаменателя.
Нули передаточной функции - корни ее числителя.
Полюса передаточной функции - корни ее знаменателя.

Преобразование Лапласа
Результатом обратного преобразования Лапласа является оригинал функции
Например

Свойства преобразования Лапласа
1. Принцип суперпозиции выполняется как для прямого, так и для обратного преобразования Лапласа
2. Изображение для производной функции f(t) равно
С помощью преобразования Лапласа можно сразу найти начальное и конечной значение функции-оригинала (при t = 0 и t →∞)

Передаточная функция после преобразования Лапласа

Пример

Пример (продолжение)

Преобразования Лапласа

Пример
Исходные данные:
Объект управления описывается уравнением:
На вход поступает сигнал x(t) = 1(t)
Найти: выходной сигнал y(t)
Решение:
Решим задачу с помощью передаточных функций и изображений сигналов по Лапласу.
X(s) = 1/s
После преобразования Лапласа уравнение объекта:
T*s*Y(s) + Y(s) = k * X(s)
W(s) = Y(s) / X(s) = k / (T*s + 1)
Y(s) = W s) * X(s) = k / (T*s^2 + s) = (k / s) - (k*T / (T*s + 1))
y(t) = k - k * exp(-t / T) при t > 0

Начальное и конечное значения функции y(t)
При ступенчатом входном сигнале 1(t)
X(s) = 1 / s
То есть

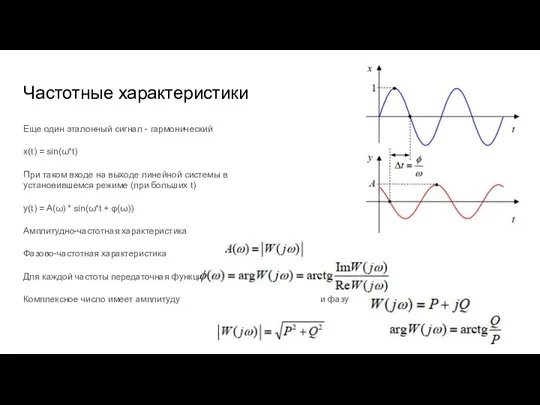
Частотные характеристики
Еще один эталонный сигнал - гармонический
x(t) = sin(ω*t)
При таком входе на выходе линейной системы в
установившемся режиме (при больших t)
y(t) = A(ω) * sin(ω*t + φ(ω))
Амплитудно-частотная характеристика
Фазово-частотная характеристика
Для каждой частоты передаточная функция - это комплексное число
Комплексное число имеет амплитуду и фазу

Основные типы звеньев
A(ω) - амплитудно-частотная характеристика АЧХ.
АЧХ - коэффициент усиления гармонического сигнала.
если A(ω) > 1, то сигнал усиливается
если A(ω) < 1, то сигнал ослабляется
φ(ω) - фазово-частотная характеристика ФЧХ
По форме АЧХ различают основные типы звеньев:
фильтр низких частот - пропускает НЧ сигналы примерно с одинаковым коэф. усиления, блокирует ВЧ шумы и помехи
фильтр высоких частот - пропускает ВЧ сигналы, блокирует НЧ сигналы
полосовое фильтр - пропускает только сигналы с частотам в полосе от w1 до w2
полосовой режекторный фильтр - блокирует только сигналы с частотами в полосе от w1 до w2, остальные пропускает

Логарифмические частотные характеристики
Вместо A(ω) было предложено использовать логарифмическую амплитудную частотную характеристику (ЛАЧХ):
график, на котором по оси абсцисс откладывается десятичный логарифм частоты lg(ω), а по оси ординат - величина Lm(ω) = 20*lg(A(ω)), измеряемая в децибелах (дБ)
При построении логарифмической фазово-частотной характеристики (ЛФЧХ) по оси обсции также откладывает логарифм частоты lg(ω)
Единица отсчета на логарифмической оси - декада - диапазон, на котором частота увеличивается в 10 рза (т.е. значение логарифма увеличивается на 1)
ЛАЧХ + ЛФЧХ = логарифмическая амплитудно-фазовая частотная характеристика ЛАФЧХ (диаграмма Боде)
Свойства логарифмических характеристик:
ЛАЧХ и ЛФЧХ для произведения W1(s)*W2(s) вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев:
20*lg A(ω) = 20*lg A1(ω) + 20*lg A2(ω)
φ(ω) = φ1(ω) +φ2(ω)
в области ВЧ и НЧ ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ±20 дБ/дек (децибел на декаду), ±40 дБ/дек и т.д.

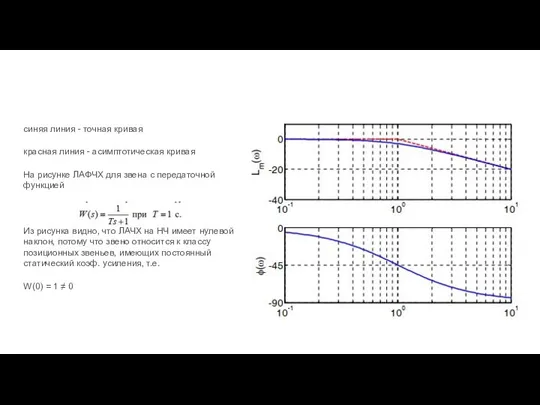
синяя линия - точная кривая
красная линия - асимптотическая кривая
На рисунке ЛАФЧХ для звена с передаточной функцией
Из рисунка видно, что ЛАЧХ на НЧ имеет нулевой наклон, потому что звено относится к классу позиционных звеньев, имеющих постоянный статический коэф. усиления, т.е.
W(0) = 1 ≠ 0

Если W(0) = 0, передаточная функция содержит множитель s^k (k > 0). В это случае наклон ЛАЧХ на НЧ будет равен k*20 дБ/дек
Если W(0) = ∞, звено содержит один или несколько интеграторов, т.е. в знаменателе есть сомножитель s^k. В это случае ЛАЧХ на НЧ имеет наклон (-k)*20 дБ/дек
Наклон ЛАЧХ на ВЧ определяется разностью степеней числителя и знаменателя передаточной функции. Если числитель имеет степень m, а знаменатель - степень n, то наклон асимптоты равен 20 * (m - n) дБ/дек.

Типовые динамические звенья. Усилитель
Звенья, имеющие конечный коэф. усиления постоянного сигнала, т.е. W(0) = k ≠ 0, называются позиционным.
Простейшее позиционное звено - идеальный (безынерционный) усилитель с передаточной функцией:
W(s) = k
Переходная характеристика h(t) = k (t > 0)
Импульсная характеристика w(t) = k * δ(t)
АЧХ A(ω) = k ФЧХ φ(ω) = 0

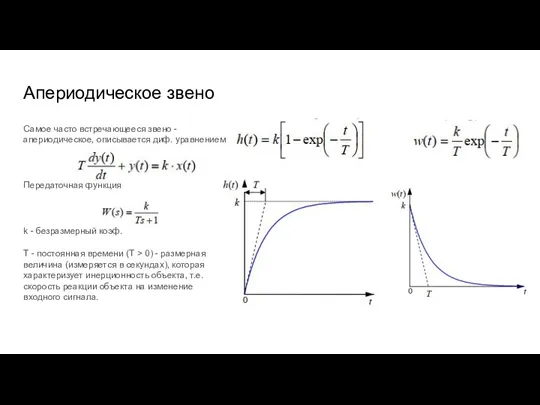
Апериодическое звено
Самое часто встречающееся звено - апериодическое, описывается диф. уравнением
Передаточная функция
k - безразмерный коэф.
Т - постоянная времени (Т > 0) - размерная величина (измеряется в секундах), которая характеризует инерционность объекта, т.е. скорость реакции объекта на изменение входного сигнала.

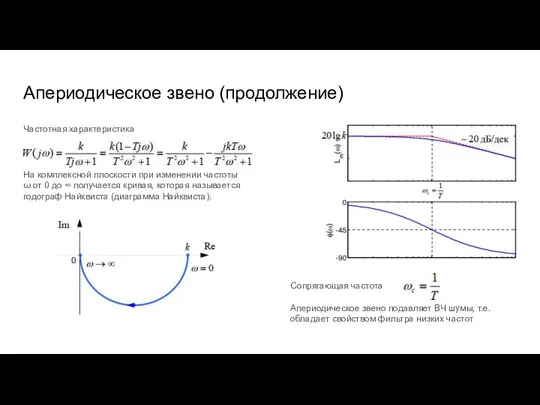
Апериодическое звено (продолжение)
Частотная характеристика
На комплексной плоскости при изменении частоты ω от 0 до ∞ получается кривая, которая называется годограф Найквиста (диаграмма Найквиста).
Сопрягающая частота
Апериодическое звено подавляет ВЧ шумы, т.е. обладает свойством фильтра низких частот

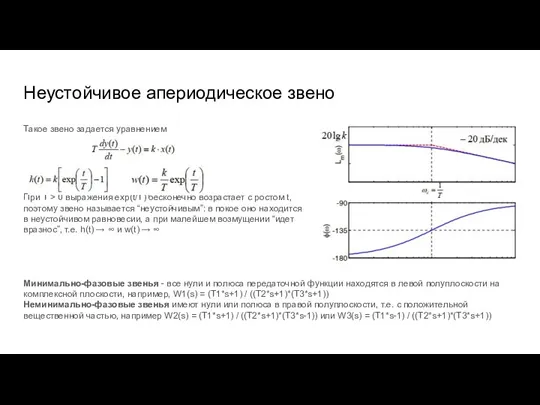
Неустойчивое апериодическое звено
Такое звено задается уравнением
При T > 0 выражения exp(t/T) бесконечно возрастает с ростом t, поэтому звено называется “неустойчивым”: в покое оно находится в неустойчивом равновесии, а при малейшем возмущении “идет вразнос”, т.е. h(t) → ∞ и w(t) → ∞
Минимально-фазовые звенья - все нули и полюса передаточной функции находятся в левой полуплоскости на комплексной плоскости, например, W1(s) = (T1*s+1) / ((T2*s+1)*(T3*s+1))
Неминимально-фазовые звенья имеют нули или полюса в правой полуплоскости, т.е. с положительной вещественной частью, например W2(s) = (T1*s+1) / ((T2*s+1)*(T3*s-1)) или W3(s) = (T1*s-1) / ((T2*s+1)*(T3*s+1))

Колебательное звено
Звено имеет передаточную функцию
при условии, что знаменатель имеет комплексно-сопряженные корни, т.е.
Передаточная функция колебательного звена
ξ - параметр затухания (0 < ξ < 1), чем больше ξ, тем быстрее затухают колебания
При ξ = 0 получается консервативное звено, которое дает незатухающие колебания на выходе.
При ξ ≥ 1 модель представляет собой апериодическое звено 2-го порядка, т.е. последовательное соединение двух апериодических звеньев
Колебательное звено относится позиционным звеньям, его статический коэф. усиления W(0) = k

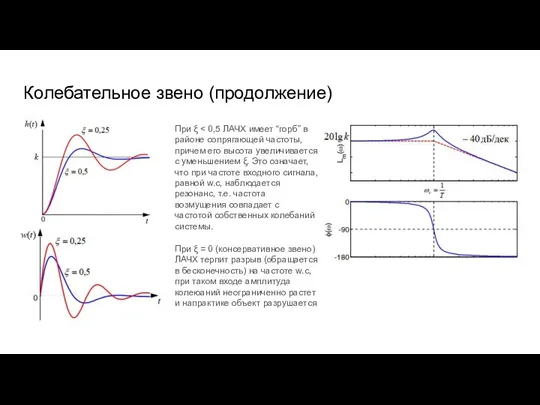
Колебательное звено (продолжение)
При ξ < 0,5 ЛАЧХ имеет “горб” в районе сопрягающей частоты, причем его высота увеличивается с уменьшением ξ. Это означает, что при частоте входного сигнала, равной w.c, наблюдается резонанс, т.е. частота возмущения совпадает с частотой собственных колебаний системы.
При ξ = 0 (консервативное звено) ЛАЧХ терпит разрыв (обращается в бесконечность) на частоте w.c, при таком входе амплитуда колеюаний неограниченно растет и напрактике объект разрушается

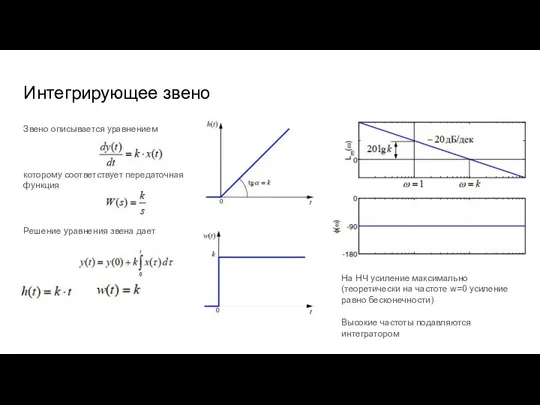
Интегрирующее звено
Звено описывается уравнением
которому соответствует передаточная функция
Решение уравнения звена дает
На НЧ усиление максимально (теоретически на частоте w=0 усиление равно бесконечности)
Высокие частоты подавляются интегратором

Дифференцирующие звенья
Дифференцирующее звено дает на выходе производную входного сигнала.
Уравнение идеального дифференцирующего звена
Операторная форма записи
Передаточная функция
Переходная характеристика
Импульсная характеристика
Это физически нереализуемые звенья, т.к. дельта-функцию и ее производную, имеющие бесконечные значения, невозможно получить на реальном устройстве.
Диф. звено реагирует не на изменение входной величины, а на изменение ее производной, т.е. на тенденцию развития событий. Поэтому говорят, что диф. звено обладает упреждающим (прогнозирующим) действием. С его помощью можно ускорсить реакцию системы.

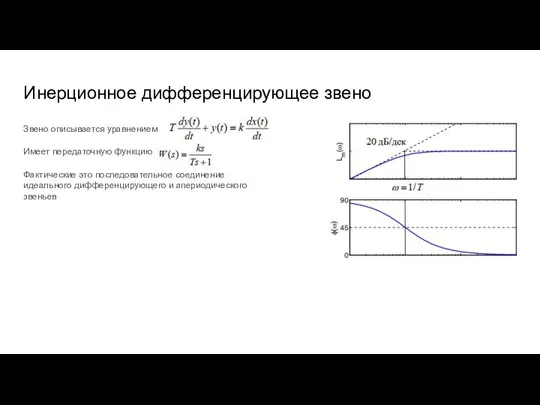
Инерционное дифференцирующее звено
Звено описывается уравнением
Имеет передаточную функцию
Фактические это последовательное соединение идеального дифференцирующего и апериодического звеньев

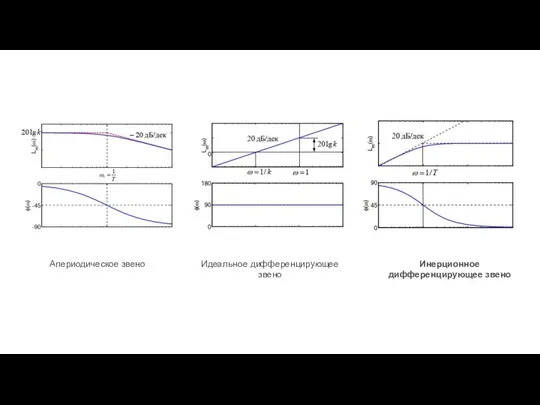
Апериодическое звено
Идеальное дифференцирующее звено
Инерционное дифференцирующее звено

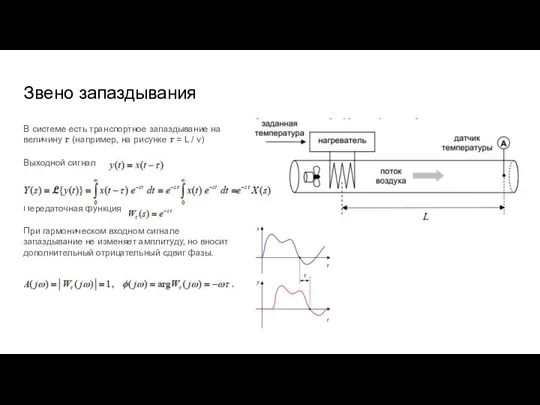
Звено запаздывания
В системе есть транспортное запаздывание на величину ? (например, на рисунке ? = L / v)
Выходной сигнал
Передаточная функция
При гармоническом входном сигнале запаздывание не изменяет амплитуду, но вносит дополнительный отрицательный сдвиг фазы.

Обратные звенья
Звено называется обратным W(s) (или инверсией звена), если задано передаточной функцией
Найдем ЛАФЧХ обратного звена по заданной ЛАФЧХ исходного звена
P(w) и Q(w) - вещественная и мнимая частотные характеристики
Для обратного звена
Для логарифмических характеристик

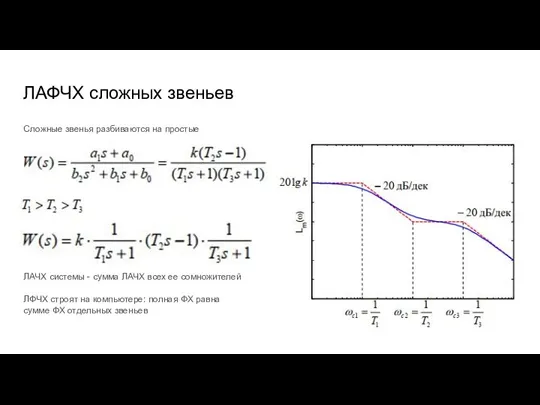
ЛАФЧХ сложных звеньев
Сложные звенья разбиваются на простые
ЛАЧХ системы - сумма ЛАЧХ всех ее сомножителей
ЛФЧХ строят на компьютере: полная ФХ равна сумме ФХ отдельных звеньев

Минимально-фазовые звенья (фаза по модулю меньше, чем фаза любого звена с такой же амплитудной характеристикой) - устойчивое апериодическое звено
Неминимально-фазовые звенья (звенья, передаточные функции которых имеют нули и полюса в правой полуплоскости, т.е. с положительной вещественной частью: например, 5+3i, 5-3i, 5+0i) - неустойчивое апериодическое звено

Структурные схемы
Две формы записи:
операторная запись: x(t), W(p), y(t)
запись в изображениях: X(s), W(s), Y(s)

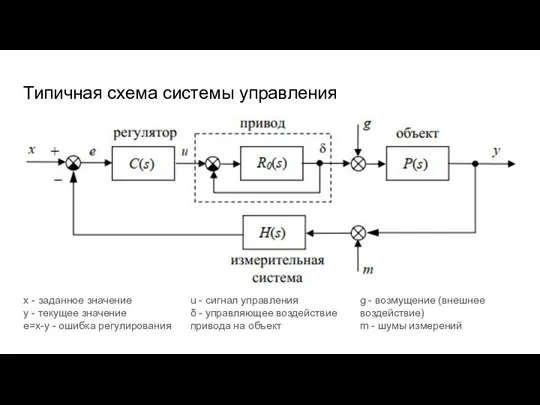
Типичная схема системы управления
x - заданное значение
y - текущее значение
e=x-y - ошибка регулирования
u - сигнал управления
δ - управляющее воздействие привода на объект
g - возмущение (внешнее воздействие)
m - шумы измерений

Правила преобразования

Преобразование отрицательной обратной связи
Если обратная связь – положительная (сигналы x и f складываются), в знаменателе будет стоять знак «минус

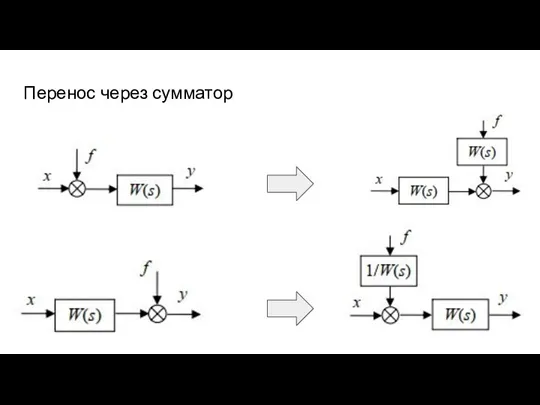
Перенос через сумматор

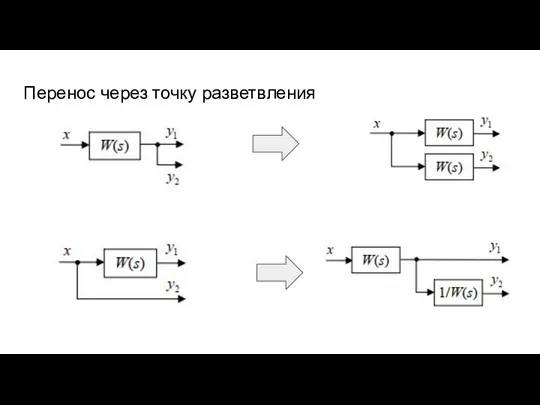
Перенос через точку разветвления

Пример преобразования типовой схемы
Сначала находят полную передаточную функцию привода с отрицательной обратной связью:
R(s) = R0(s) / (1+R0(s))
Далее находят ПФ от входа x ко всем выходам. Для этого все остальные выходы считают нулевыми и удаляют со схемы.
В системе 3 входа: x, g, m
В системе в качестве выходов рассматривают: y, u, e
Соответственно, всего 9 передаточных функций (отношение выхода ко входу):
y/x, u/x, e/x, y/g, u/g, e/g, y/m, u/m, e/m

Передаточные функции от входа Х к выходам
Считаем, что G(s)=0, M(s)=0

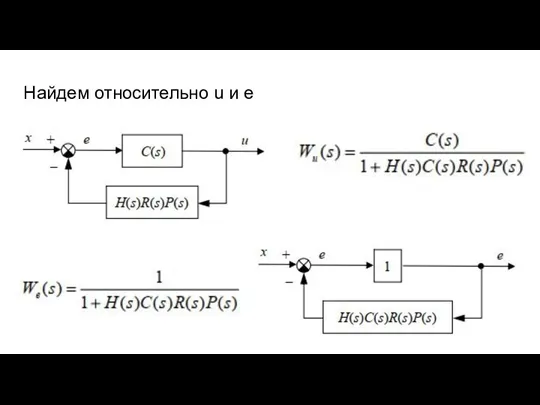
Найдем относительно u и e

Анализ систем управления

Требования к управлению
Основные требования:
Точность - в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка не должна превышать допустимую
Устойчивость - системы должна оставаться устойчивой на всех режимах, не должна идти “вразнос”
Качество переходных процессов - при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно
Робастность - система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировани

Процесс на выходе
При нулевых начальных условиях
Y(s) = W(s) * X(s),
где W(s) = n.w(s) / Δ(s) и X(s) = n.x(s) / d.x(s)
Будем считать, что полиномы Δ(s) и d.x(s) имеют только простые вещественные корни.
Полиномы рациональных функций W(s) и X(s)
Δ(s) = (s - α1) * (s - α2) * (s - α3)...(s - αn)
d.x(s) = (s - β1) * (s - β2) * (s - β3)...(s - βm)
αi и βi - полюса рациональных функций W(s) и X(s)
Выводы:
сигнал на выходе зависит как от свойств передаточной функции системы, так и входного сигнала
для того, чтобы переходной процесс затухал (y(t)→0), все αi и βi должны быть отрицательными (иметь отрицательные вещественные части)
если один из полюсов W(s) или X(s) равен нулю, то y(t) может иметь постоянную (не затухающую) составляющую
если хотя бы один из полюсов W(s) или X(s) больше нуля (имеет положительную вещественную часть), выход системы неограниченно растет

Характеристический полином
Если среди корней полинома Δ(s) есть числа с положительной вещественной частью, то сигнал выхода будет неограниченно возрастать при любом входном воздействии, для которого произведение W(s)*X(s) несократимо.
Δ(s) - характеристический полином, так как расположение его корней определяет устойчивость (или неустойчивость) системы
Например, выход системы неограниченно расчет, если:
Δ(s) = (s - 2) * (s + 1)
Δ(s) = (s - 2) * (s - 1)
Δ(s) = (s - 2) * 10

Точность
Точность системы оценивается для одного из эталонных сигналов.
Единичный ступенчатый сигнал:
Линейно-возрастающий сигнал:
Гармонический сигнал с частотой w
Точность системы в установившемся режиме определяется e(t) или ее изображением E(s).
Для ее исследования используют ПФ по ошибке We(s): E(s) = We(s) * X(s)
C(s) = n.c(s) / d.c(s) P(s) = n(s) / d(s) X(s) = n.x(s) / d.x(s)
Передаточная функция по ошибке:
We(s) = 1 / (1 + C(s)*P(s)) = d.(s) * d(s) / Δ(s)
где Δ(s) - характеристический полином замкнутой системы
Δ(s) = d.c(s) * d(s) + n.c(s) * n(s)

Реакция системы на 1(t)
Единичный ступенчатый сигнал 1(t) имеет изображение X(s) = 1/s
Сигнал ошибки определяется полюсами We(s) (т.е. корнями характеристического полинома Δ(s)) и полюсами X(s)
Все полюса We(s) должны иметь отрицательные вещественные части, иначе система будет неустойчивой. Нулевых полюсов у We(s) быть не может.
Y0(s) имеет полюса только с отрицательной вещественной частью, а постоянная b рассчитывается по формуле разложения на простые дроби:
Чтобы сделать нулевой статическую ошибку, достаточно обеспечить d.c(0) = 0 (т.е. регулятор должен содержать интегратор) или d(0) = 0 (т.е. объект содержит интегратор)
Этот результат можно обобщить для любых незатухающих сигналов входных сигналов, изображения которых имеют полюса на мнимой оси (например, в точке s = 0 или s = ±j*w). Для того, чтобы ошибка стремилась к нулю при t → ∞ необходимо, чтобы эти полюса сократились в произведении

Устойчивость
Устойчивая система возвращается в состояние равновесия, если какая-то сила ее из этого состояния выведет
А - устойчивое положение равновесия
Б, В - неустойчивое положение равновесия
Г, Д - нейтральное (нейтрально устойчивое) положение равновесия
Для системы шарик-горка:
устойчивость - не свойство системы, а свойство некоторого положения равновесия
может быть несколько положений равновесия, из них некоторые - устойчивые, а некоторые - нет
положение равновесия может быть устойчиво при малых отклонениях (система устойчива “в малом”) и неустойчива при больших (“в большом”)

Разновидности устойчивости
устойчивость “вход-выход” - если рассматривается только выход системы при различных ограниченных входах
устойчивость автономной системы, на которую не действуют внешние сигналы (все входы нулевые). Такую систему вывели из положения равновесия (задали ненулевые начальные условия) и “отпустили”. Если система сама возвращается в исходное положение равновесия, то система устойчива.
Если при этом рассматривается только только выход системы (а не ее внутренние сигналы), то говорят о технической устойчивости (или устойчивости по выходу)
Если при этом не только выход, но и все внутренние переменные (переменные состояния) приближаются к своими значениям в положении равновесия, то говорят о внутренней или математической устойчивости
устойчивость процессов - все такие системы нелинейные и очень сложные

Устойчивость “вход-выход”
Система “идет вразнос” - управляемая величина растет неограниченно при всех допустимых входных сигналах
Если система обладает устойчивостью “вход-выход”, если “не идет вразнос”
Устойчивость “вход-выход” не учитывает внутренние переменные процессы в системе (объекте), а учитывает только вход и выход.
Например, модель интегрирующего звена (ванна с включенным краном), в котором входной сигнал (например, входной поток воды из крана) имеет постоянное (ограниченное по величине) значение не обладает устойчивостью “вход-выход”

Техническая устойчивость
Техническая устойчивость относится к автономной системе, у которой все входные сигналы равны нулю (в отличие от устойчивости “вход-выход”)
Положение равновесия - состояние системы, которая находится в покое, т.е. выходной сигнал y(t) постоянная величина и все производные dy(t) / dt = 0
Если системы выводят из положения равновесия и убирают все возмущения, то система может быть:
устойчивой, т.е. при t→∞ система возвращается в исходное положение равновесия
нейтрально устойчивой, т.е. если выходная координата остается ограниченной (не уходит в бесконечность)
неустойчивой, т.е. если выход становится бесконечным

Внутренняя устойчивость
При рассмотрении внутренней устойчивости учитывают не только выход, но и все переменные, описывающие состояние системы.
x(t) - вектор состояния системы
Уравнение движения системы:
Если вектор состояния x(t) состоит из двух компонент x1(t) и x2(t), то уравнение движения системы:
Для нелинейной системы может быть несколько положений равновесия, причем некоторые могут быть устойчивы, а другие - нет

Асимптотическая устойчивость
x(t) - все движения системы
x* - положение равновесия
Устойчивость системы означает, что все движения x(t), которые начинаются близко от положения равновесия x*, при всех t остаются в некоторой окрестности x*.
Система обладает асимптотической устойчивостью при условии, что система не просто устойчива, а еще и возвращается в положение равновесия, т.е. x(t)→x* при t→∞
а) асимптотически устойчивая система
б) неустойчивая система

Внутренняя устойчивость (устойчивость по Ляпунову)
Рассмотрим систему с одной переменной состояния x(t).
Система называется устойчивой по Ляпунову в положении равновесия x*, если при начальном отклонении от положения равновесия x* не более, чем на δ, траектория движения x(t) отклоняется от x* не более, чем на ε, причем для каждого ε можно найти соответствующую ему δ(ε)
|x0 - x*| < δ |x(t) - x*| < ε при всех t > 0
Система асимптотически устойчивая, если |x(t) - x*| → 0 при при t→∞. Однако выполнение сходимости этого условия не означает устойчивость по Ляпунову.
Асимптотическая устойчивость - более сильное требование. Положения равновесия, которые устойчивы по Ляпунову, но не асимптотически устойчивы, называют нейтрально устойчивыми
Положение равновесия неустойчиво, если для него не выполняется условие устойчивости Ляпунова.

Устойчивость линейных систем
Особенности линейных систем:
автономная линейная система (на которую не действуют внешние силы) может иметь единственное положение равновесия (в котором все сигналы равны нулю) или бесконечно много положений равновесия (шарик на плоской плоскости)
устойчивость - это свойство линейной системы, но не отдельного положения равновесия: или все ее движения устойчивы (асимптотическая устойчивость), или все неустойчивы
асимптотическая устойчивость линейной системы “в малом” сразу означает ее устойчивость “в целом”, т.е. при любых отклонениях от положения равновесия
асимптотически устойчивая система обладает устойчивостью “вход-выход”, а просто устойчивая система (нейтрально устойчивая, не асимптотически устойчивая) - нет

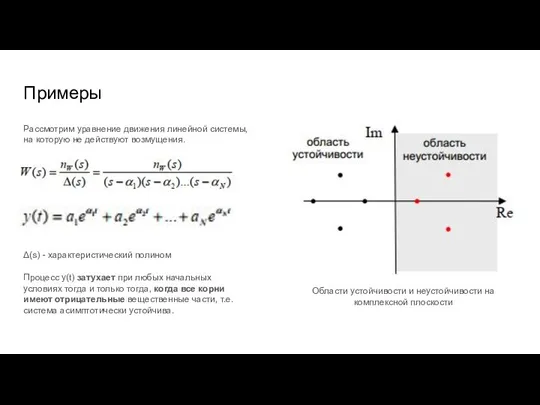
Примеры
Рассмотрим уравнение движения линейной системы, на которую не действуют возмущения.
Области устойчивости и неустойчивости на комплексной плоскости
Δ(s) - характеристический полином
Процесс y(t) затухает при любых начальных условиях тогда и только тогда, когда все корни имеют отрицательные вещественные части, т.е. система асимптотически устойчива.

Примеры
При отсутствии внешних возмущений выход системы:
Выход системы содержит постоянное слагаемое a1. Поэтому такая система называется нейтрально устойчивой.
Предположим, что один из корней полинома Δ(s) равен 0, а остальные имеют отрицательную вещественную часть. Это значит, что система содержит интегрирующее звено.
Учитывая, что при всех t

Примеры
Допустим, что характеристический полином Δ(s) имеет две мнимых корня: α1 = 0 + j*w и α2 = 0 - j*w.
Это значит, что система содержит консервативное звено - генератор колебаний.
Слагаемые могут быть представлены в виде:
Эти составляющие дают незатухающие колебания, поэтому системы находится на границе устойчивости (нейтрально устойчива).

Устойчивость линеаризованных систем
Устойчивость нелинейной системы можно оценить в помощью линеаризованной системы. Для этого применяют теоремы Ляпунова, которые связывают корни характеристического полинома Δ(s) линейной модели и устойчивость нелинейной системы в окрестности точки линеаризации:
если все корни имеют отрицательные вещественный части, то нелинейная система также устойчива
если есть хотя бы один корень с положительной вещественной частью, то нелинейная система неустойчива
если нет корней с положительной вещественной частью, но есть хотя бы один корень с нулевой вещественной частью, то об устойчивости нелинейной системы ничего нельзя сказать без дополнительного исследования

Критерий Гурвица
Можно проверить устойчивость полинома, не вычисляя его корни.
Необходимое условие устойчивости полинома: все коэффициенты (a0, a1, a2 ...) должны быть одного знака (обычно положительного).
Однако при n>2 это условие недостаточно, если полином имеет комплексно-сопряженные корни.
Критерий Гурвица использует матрицу Hn размером n×n, составленную из коэффициентов полинома Δ(s) следующим образом:
первая строка содержит коэффициенты
a1, a3, a5, ... (все с нечетными номерами), оставшиеся элементы заполняются нулями
вторая строка содержит коэффициенты
a0, a2, a4, … (все с четными номерами)
третья и четвертая строка получаются сдвигом первой и второй строк на 1 позицию вправо, и т.д.
Критерий Гурвица. Все корни полинома Δ(s) имеют отрицательные части тогда и только тогда, когда все n главных миноров матрицы Hn (определителей Гурвица) положительны

Пример матрицы Гурвица

Пример
W(s) = nw(s) / Δ(s)
W(s) = (5*s^2+s-10) / (1*s^3+2*s^2+3*s+4)
Δ(s) = 1*s^3+2*s^2+3*s^1+4*s^0
Матрица Гурвица H3:
2 4 0
1 3 0
0 2 4
Все коэффициенты (1, 2, 3, 4) > 0
D1 = 2 > 0
D2 = (2*3 - 4*1) = 2 > 0
Вывод. Все корни полинома имеют отрицательную вещественную часть - система устойчива.

Правило: Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

Критерий Найквиста
Критерий Найквиста позволяет определить устойчивость замкнутой системы, построив частотную характеристику разомкнутой системы
L(s) - передаточная функция разомкнутой системы
L(jω) - частотная характеристика разомкнутой системы
Пусть разомкнутая система L(s) устойчива и не содержит интегрирующих звеньев, т.е. L(0) = K ≠ ∞
Для каждой частоты w значение L(jω) - это комплексное число, которое можно изобразить точкой на комплексной плоскости. При изменении частоты ω от 0 до ∞ из этих точек складывается годограф Найквиста.

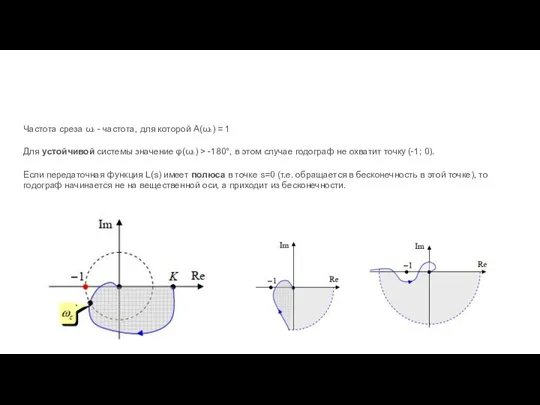
Годограф Найквиста
Годограф Найквиста - кривая, которая начинается в точке (K; 0) на вещественной оси и заканчивается в начале координат (если L(s) - строго правильная функция, т.е. степень числителя меньше степени знаменателя).
Критерий Найквиста. Система устойчива тогда и только тогда, когда годограф L(jω) не охватывает точку (-1; 0). Если частотная характеристика проходит через точку (-1; 0), то система находится на границе устойчивости, т.е. A(ω) = 1 и φ(ω) = -180°

Частота среза ωc - частота, для которой A(ωc) = 1
Для устойчивой системы значение φ(ωc) > -180°, в этом случае годограф не охватит точку (-1; 0).
Если передаточная функция L(s) имеет полюса в точке s=0 (т.е. обращается в бесконечность в этой точке), то годограф начинается не на вещественной оси, а приходит из бесконечности.

Система с запаздыванием
Если в системе есть запаздывание на время τ, на любой частоте появляется дополнительный сдвиг фазы -τw (без изменения амплитуды), т.е. каждая точка годографа поворачивается на некоторый угол против часовой стрелки.
В данном случае, запаздывание привело к неустойчивости системы (годограф охватил точку (-1;0)).
Например, медленный датчик может привести к потере устойчивости системы!
синяя линия - ЧХ системы без запаздыванием
красная линия - ЧХ системы с запаздыванием

Пример годографа системы
Если L(s) имеет полюса с положительной вещественной частью (разомкнутая система неустойчива), нужно считать, сколько раз годограф пересекает ось абсцисс левее точки (−1; 0). Причем переходы «сверху вниз» считаются положительными, а переходы «снизу вверх» - отрицательными. Для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы разница между числом положительных и отрицательных переходов была равна L / 2 , где L – число неустойчивых полюсов функции L(s) .
Начальная точка на оси абсцисс левее точки (−1; 0) считается за половину перехода. На рисунке показаны годографы устойчивых систем для случая L = 1.
Частотная характеристика начинается на вещественной оси левее точки (−1; 0) . На рисунке слева годограф сначала идет вниз (половина положительного перехода) и больше нигде не пересекает ось абсцисс левее точки (−1; 0) , поэтому разница переходов равна (+½) = L/2 и замкнутая система устойчива.
На правом рисунке частотная характеристика сначала идет вверх (считаем это за половину отрицательного перехода), а затем переходит в нижнюю полуплоскость (положительный переход). Разница снова равна (-½ + 1) = L/2 и система устойчива.

Критерий Найквиста для ЛАФЧХ
Сначала предположим, что передаточная функция разомкнутой системы не имеет неустойчивых полюсов. Как мы уже знаем, для анализа устойчивости наиболее важно поведение частотной характеристики в районе частоты среза ωc , где A(ωc) = 1 и Lm(ωc) = 20lg A(ωc) = 0.
Если разомкнутая система имеет неустойчивые звенья, нужно считать переходы фазовой характеристики через линию φ(ω) = −180° левее частоты среза. Здесь положительным считается переход снизу вверх, а отрицательным – сверху вниз. Если фазовая характеристика начинается на линии φ(ω) = −180° (на нулевой частоте), это считается за половину перехода. Для устойчивой системы разность между числом положительных и отрицательных переходов должна быть равна L/2, где L – число неустойчивых полюсов передаточной функции L(s) .
Для устойчивой системы значение фазы на частоте среза должно быть больше, чем −180°. На графике представлены три фазовых характеристики устойчивых систем. Кривая 1 соответствует случаю, когда в разомкнутой системе нет интеграторов (и фазовая характеристика начинается с нуля), кривая 2 – системе с одним интегратором, а кривая 3 – c двумя.

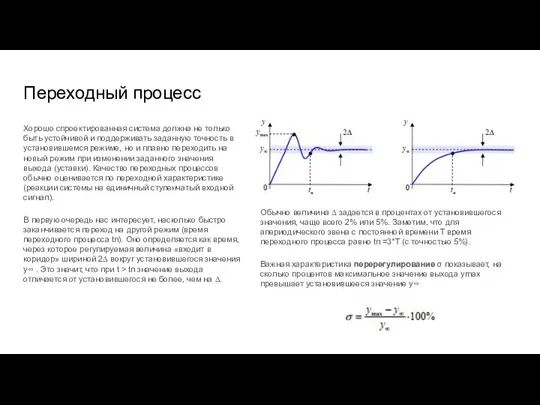
Переходный процесс
Хорошо спроектированная система должна не только быть устойчивой и поддерживать заданную точность в установившемся режиме, но и плавно переходить на новый режим при изменении заданного значения выхода (уставки). Качество переходных процессов обычно оценивается по переходной характеристике (реакции системы на единичный ступенчатый входной сигнал).
В первую очередь нас интересует, насколько быстро заканчивается переход на другой режим (время переходного процесса tп). Оно определяется как время, через которое регулируемая величина «входит в коридор» шириной 2∆ вокруг установившегося значения y∞ . Это значит, что при t > tп значение выхода отличается от установившегося не более, чем на ∆.
Обычно величина ∆ задается в процентах от установившегося значения, чаще всего 2% или 5%. Заметим, что для апериодического звена с постоянной времени T время переходного процесса равно tп =3*T (с точностью 5%).
Важная характеристика перерегулирование σ показывает, на сколько процентов максимальное значение выхода ymax превышает установившееся значение y∞

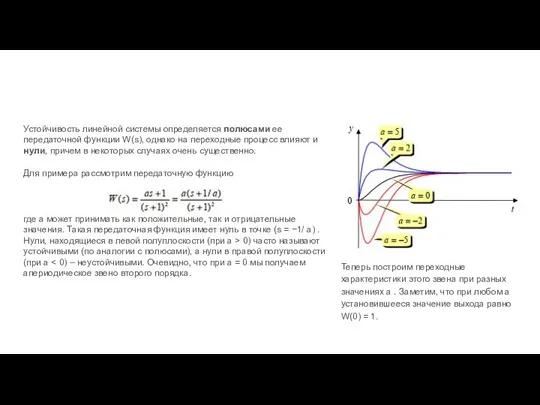
Устойчивость линейной системы определяется полюсами ее передаточной функции W(s), однако на переходные процесс влияют и нули, причем в некоторых случаях очень существенно.
Для примера рассмотрим передаточную функцию
где a может принимать как положительные, так и отрицательные значения. Такая передаточная функция имеет нуль в точке (s = −1/ a) . Нули, находящиеся в левой полуплоскости (при a > 0) часто называют устойчивыми (по аналогии с полюсами), а нули в правой полуплоскости (при a < 0) – неустойчивыми. Очевидно, что при a = 0 мы получаем апериодическое звено второго порядка.
Теперь построим переходные характеристики этого звена при разных значениях a . Заметим, что при любом a установившееся значение выхода равно W(0) = 1.

Частотные оценки качества
Качество системы можно оценивать не только во временнóй области (переходный процесс во времени), но и в частотной (по частотной характеристике).
Из частотных оценок наиболее важны запасы устойчивости:
запасы устойчивости по амплитуде
запасы устойчивости по фазе
запасы устойчивости по ЛЧХ
кратчайшее расстояние от годографа до точки (-1;0)
показатель колебательности

Запасы устойчивости по амплитуде
Обычно рассматривают запасы устойчивости по амплитуде и по фазе. Запас устойчивости по амплитуде g.m – это дополнительное усиление контура, которое необходимо, чтобы вывести систему на границу области устойчивости. Эта величина измеряется в децибелах
Запас по амплитуде вычисляется по формуле
где A.g - амплитудная характеристика на частоте w.g, где фазовая характеристика равна -180°. На практика нужно обеспечить запас по амплитуде не менее 6 дБ

Запасы устойчивости по фазе
Запас устойчивости по фазе φ.m - это дополнительный сдвиг фазы (поворот частотной характеристики против часовой стрелки), который необходим для того, чтобы вывести систему на границу устойчивости. Этот сдвиг определяется на частоте среза w.c, где A(w.c) = 1. Запас устойчивости должен быть не менее 30°.
Если в системе есть запаздывание на время τ , каждая точка годографа частотной характеристики дополнительно поворачивается против часовой стрелки на угол, равный τ.ω для частоты ω .
Поэтому запасы устойчивости (как по амплитуде, так и по фазе) уменьшаются. На рисунке синяя линия соответствует системе без запаздывания, а красная – той же системе с запаздыванием. Видно, что во втором случае запасы устойчивости существенно меньше

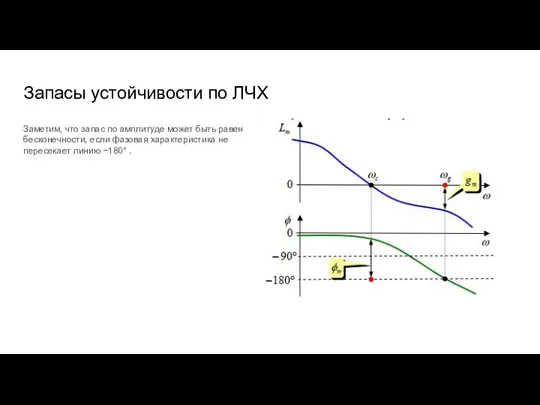
Запасы устойчивости по ЛЧХ
Заметим, что запас по амплитуде может быть равен бесконечности, если фазовая характеристика не пересекает линию −180° .

Кратчайшее расстояние от годографа до точки (-1;0)
К сожалению, в некоторых случаях классические запасы устойчивости (по амплитуде и фазе) дают не совсем верное представление о том, насколько система действительно близка к границе устойчивости. Поэтому в качестве единой характеристики иногда используют кратчайшее расстояние γ от годографа до точки (−1; 0)

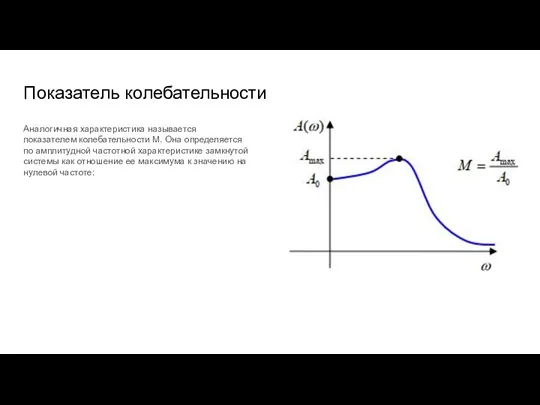
Показатель колебательности
Аналогичная характеристика называется показателем колебательности M. Она определяется по амплитудной частотной характеристике замкнутой системы как отношение ее максимума к значению на нулевой частоте:

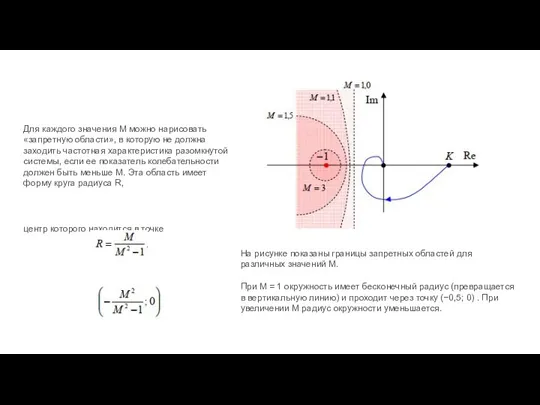
Для каждого значения M можно нарисовать «запретную области», в которую не должна заходить частотная характеристика разомкнутой системы, если ее показатель колебательности должен быть меньше М. Эта область имеет форму круга радиуса R,
центр которого находится в точке
На рисунке показаны границы запретных областей для различных значений M.
При M = 1 окружность имеет бесконечный радиус (превращается в вертикальную линию) и проходит через точку (−0,5; 0) . При увеличении M радиус окружности уменьшается.

Корневые оценки качества
Прежде всего, все корни характеристического полинома ∆(s) для устойчивой системы должны находиться на комплексной плоскости в левой полуплоскости, то есть слева от мнимой оси.
Быстродействие системы определяется степенью устойчивости η – так называется расстояние мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней). Этот корень (1) называется доминирующим, он определяет самые медленные движения в системе и время переходного процесса, которое может быть примерно рассчитано по формуле
Корни 2, 3 и 4 соответствуют более быстрым движениям
Степень устойчивости, несмотря на название, ничего не говорит о близости системы к границе устойчивости, она только характеризует быстродействие.

Колебательность
Параметр, определяющий скорость затухания колебаний в системе, называется колебательностью.
Колебательность µ для пары комплексно-сопряженных корней α ± jβ вычисляется как отношение мнимой и вещественной частей корня (по модулю):
Чем больше эта величина, тем слабее затухают колебания, вызванные этими корнями, за 1 период колебаний.
Линии постоянной колебательности – это лучи, выходящие из начала координат. При проектировании систем обычно требуется обеспечить быстродействие не ниже заданного (степень устойчивости не меньше заданной ηmin ) и колебательность не выше заданной µmax. Эти условия определяют усеченный сектор на комплексной плоскости.

Робастность
Робастность (грубость) - свойство, которое определяет нечувствительность к малым ошибкам моделирования объекта и возмущений.
Задачи, связанные с робастностью:
робастная устойчивость – обеспечить устойчивость системы при всех допустимых отклонениях модели объекта от номинальной;
робастное качество – обеспечить устойчивость и заданные показатели качества системы при всех допустимых отклонениях модели объекта от номинальной;
гарантирующее управление – обеспечить заданные показатели качества системы при всех допустимых отклонениях модели возмущения от номинальной (считая, что модель объекта известна точно).
Для того, чтобы исследовать робастность системы, нужно как-то определить возможную ошибку моделирования (неопределенность). Ее можно задать различными способами.

Параметрическая неопределенность
Параметрическая неопределенность означает, что структура модели известна, а параметры могут отличаться от номинальных, например:
где k0 и T0 - номинальные значения коэффициента усиления и постоянной времени, а ε1 и ε2 - малые ошибки моделирования
Предположим, что такой объект управляется регулятором-усилителем с передаточной функцией C(s) = K . Тогда характеристический полином замкнутой системы принимает вид
Робастный регулятор должен обеспечивать устойчивость этого полинома при всех допустимых ε1 и ε2.
В данном случае условия устойчивости сводятся к тому, что коэффициенты полинома, (T0 + ε2) и (1+ K*(k0 + ε1), имеют одинаковый знак (оба положительные или оба отрицательные).
Будем считать, что k0 > 0 и T0 > 0, а отклонения ε1 и ε2 малы в сравнении с k0 и T0 соответственно. Таким образом, T0 + ε2 > 0 при всех возможных ε2 . Следовательно, замкнутая система устойчива при
Наибольшее значение в правой части последнего неравенства будет при максимальном значении ε1 , поэтому условие робастной устойчивости принимает вид

Непараметрическая неопределенность
Непараметрическая неопределенность задает допустимую ошибку в частотной области, т.е. ошибку в частотных характеристиках. Для номинальной модели P0(jω) различают аддитивную неопределенность (абсолютную ошибку) ∆a(jω)
и мультипликативную неопределенность (относительную ошибку) ∆m(jω)
Для мультипликативной неопределенности известен очень простой критерий робастной устойчивости:
система с регулятором C(s) и номинальным объектом P0(s) робастно устойчива, если для любой частоты ω выполняется неравенство
где W0(s) - передаточная функция номинальной замкнутой системы
Этот результат называется теоремой о малом коэффициенте усиления. При этом также требуется, чтобы реальная и номинальная модели объекта, P(s) и P0(s), имели одинаковые неустойчивые полюса, то есть неопределенность не должна вносить новые источники неустойчивости.