Презентация что такое моделирование с примерами

модель нужна для понимания внутренней структуры исследуемого объект, процесса или явления, выявления основных свойств, законов развития и взаимодействия с окружающим миром
Цели моделирования
модель нужна для управления объектом, процессом или явлением, определения оптимальных способов управления при заданных целях и критериях
модель нужна для прогнозирования прямые и косвенные последствия реализации заданных способов и форм воздействия на объект, процесс или явление

Структура математических моделей
Внутренние параметры объекта (G)
Входные
параметры (X)
Выходные
параметры (Y)
Математическая модель объекта может представлять собой соотношение вида
Y = F(X, G)

Свойства математических моделей
Точность
Адекватность
Экономичность
Продуктивность
Робастность
Наглядность
Полнота
Полнота модели позволяет отразить
в достаточной мере именно те характеристики и особенности объекта, которые ин­тересны с точки зрения
поставленной цели проведения вычислительного эксперимента
Экономичность модели оценивают затратами на вычисли­тельные ресурсы (машинное время и память), необходимые для реализации модели на ЭВМ.
Эти затраты зависят от раз­мерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов.
Наглядность модели является ее желательным, но необя­зательным свойством.
Использование математических моделей и их модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл.
Робастность модели характеризует ее устойчивость по отноше­нию к погрешностям исходных данных, способность их нивели­ровать и не допускать чрезмерного влия­ния на результат численного эксперимента
Продуктивность модели связана с возможностью распола­гать достаточно достоверными исходными данными

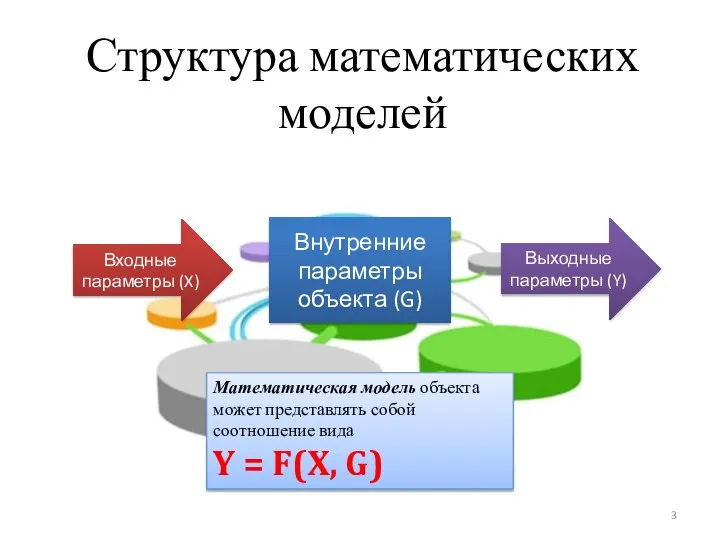
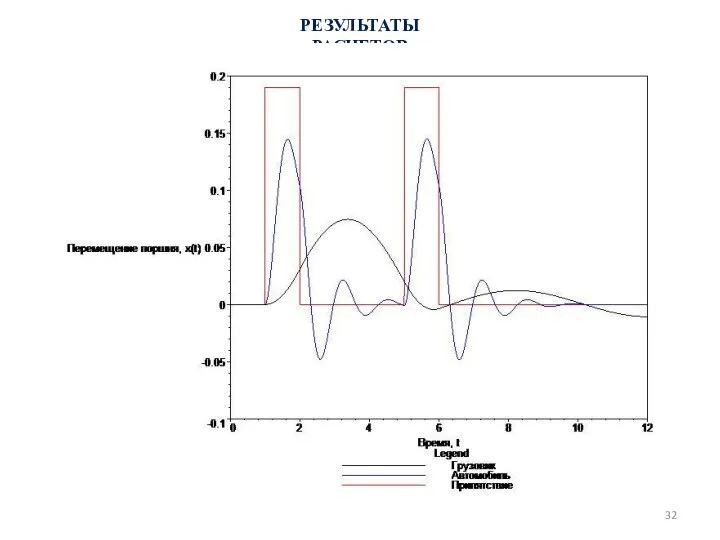
Динамической моделью называется модель, описывающая изменение параметров моделируемого объекта с течением времени x(t), g(t), y(t)
и влияние его инерци­онных свойств.
Если интересующие нас выходные параметры объекта
изменя­ются медленно и в рассматриваемый фиксированный момент времени
таким изменением можно пренебречь,
то говорят о квазистационарной математической модели.
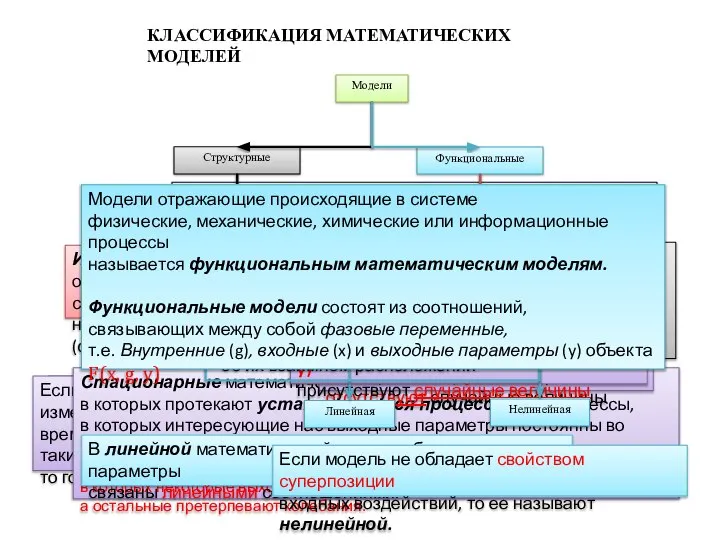
Стационарные математические модели описывают объекты,
в которых протекают установившиеся процессы, т.е. процессы,
в которых инте­ресующие нас выходные параметры постоянны во времени.
*К установившимся процессам относят и периодические процессы,
в кото­рых некоторые выходные параметры y остаются неизменными,
а остальные претерпевают колебания.
Модель называют детерминированной
если среди ее фазовых переменных
отсутствуют случайные величины
Модель называют стохастической
если среди ее фазовых переменных (x, g, y)
присутствуют случайные величины
Аналитическими моделями называются модели,
которые имеют аналитические связи
между фазовыми переменными модели
Ими­тационной математической моделью называется описание
сложных объектов при помощи совокупности его реакций
на некоторые известные (или заданные) входные воздействия (сигналы)
Геометрическая модель дополнительно к информации,
пред­ставленной в топологической модели,
содержит сведения о форме
и размерах объекта и его элементах,
об их взаимном расположении
Топологические модели отображают состав объекта
и связи между его элементами
Если модель отображает устройство объекта
и связи между составляющими его элементами,
то ее называют структурной математиче­ской моделью.
Модели
Структурные
Функциональные
Топологические
Геометрические
Имитационная
Аналитическая
Стохастические
Детерминированные
Динамические
Квазистационарные
Стационарные
Линейная
Нелинейная
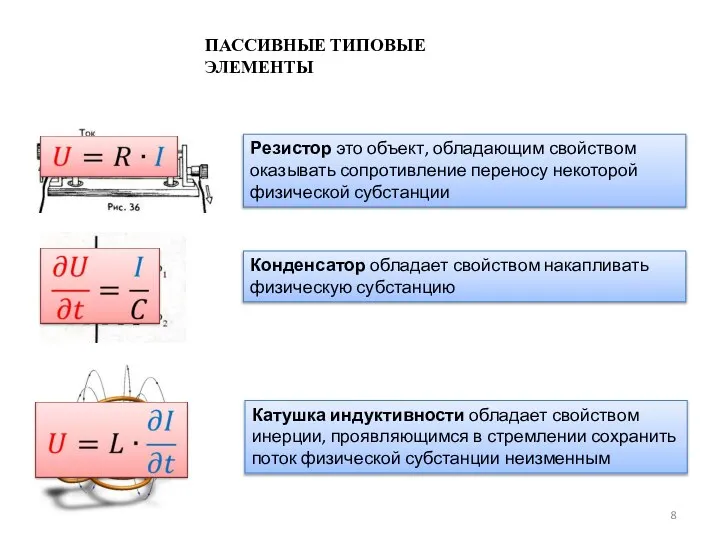
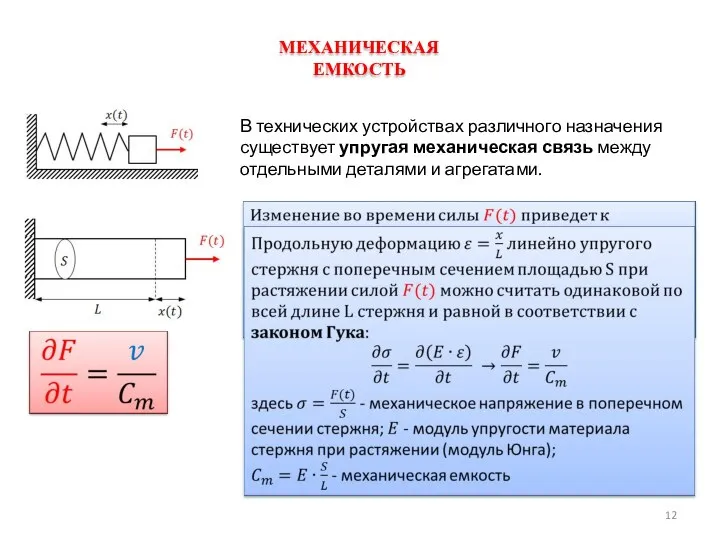
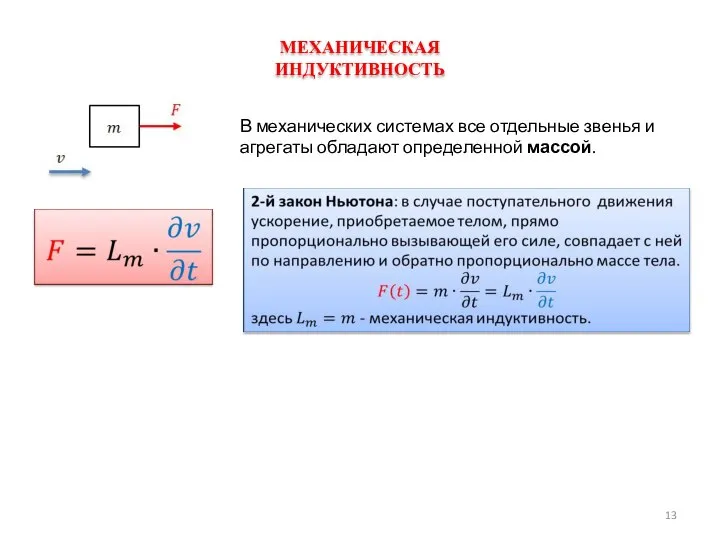
В линейной математической модели объекта его параметры
связаны линейными соотношениями.
Если модель не обладает свойством суперпозиции
входных воздействий, то ее называют нелинейной.
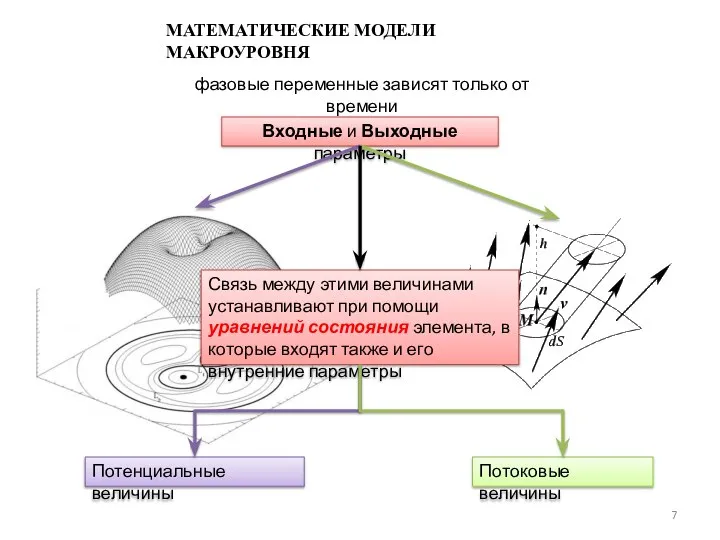
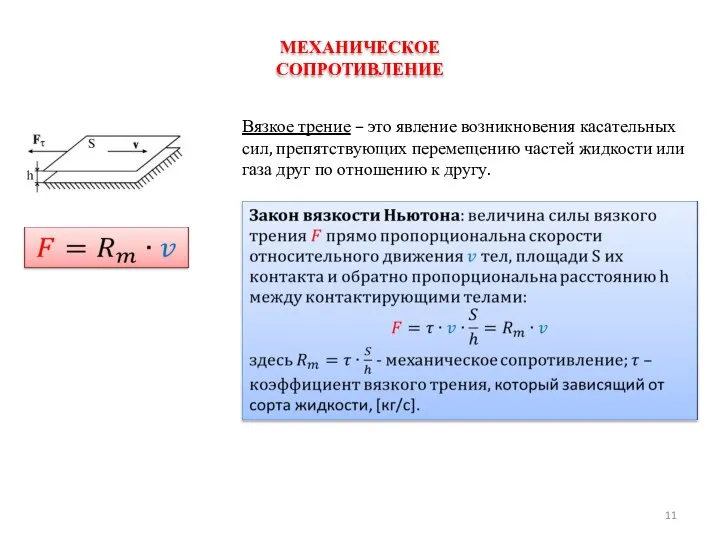
Модели отражающие происходящие в системе
физические, механические, химические или информационные процессы
называется функциональным математиче­ским моделям.
Функциональные модели состоят из соотношений,
связываю­щих между собой фазовые переменные,
т.е. Внутренние (g), входные (x) и выходные параметры (y) объекта
F(x, g, y)
КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Метауровень
Микроуровень
Макроуровень
степень детализации
Иерархи­ческие уровни отражают степень детализации описания про­цессов, протекающих в объектах, его блоках или элементах
Модели метауровня не рассматривают внутренние параметры элементов, ограничи­ваясь лишь описанием взаимных связей между укрупненными элементами системы в целом
Математические модели ма­кроуровня описывают системы с сосредоточенными параметрами
Математические модели микроуровня описывают процессы в системах с распределенными параметрами (в кон­тинуальных системах)

фазовые переменные зависят только от времени
Потенциальные величины
Потоковые величины
Входные и Выходные параметры
Связь между этими величинами устанавливают при помощи уравнений состояния элемента, в которые входят также и его внутренние параметры
МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАКРОУРОВНЯ

ПАССИВНЫЕ ТИПОВЫЕ ЭЛЕМЕНТЫ
Резистор это объект, обладающим свойством оказывать сопротивление переносу некоторой физической суб­станции
Конденсатор обладает свойством накапливать физическую субстанцию
Катушка индуктивности обладает свойством инерции, проявляющимся в стремлении сохранить поток физической субстанции неизменным

АКТИВНЫЕ ТИПОВЫЕ ЭЛЕМЕНТЫ
Идеальный источник потенциальной величины является объект или устройство, у которого выходная потенциальная величина не зависит от его входной потоковой величины
Идеальный источник потоковой величины является объект или устройство, у которого выходная потоковая величина не зависит от его входной потенциальной величины

В механических системах физическая субстанция это масса тел
Потоковая величина - скорость
Потенциальная величина - сила
МЕХАНИЧЕСКИЕ СИСТЕМЫ

Вязкое трение – это явление возникновения касательных сил, препятствующих перемещению частей жидкости или газа друг по отношению к другу.
МЕХАНИЧЕСКОЕ СОПРОТИВЛЕНИЕ

В технических устройствах различного назначения существует упругая механи­ческая связь между отдельными деталями и агрегатами.
МЕХАНИЧЕСКАЯ ЕМКОСТЬ

В механических системах все отдельные звенья и агрегаты обладают определенной массой.
МЕХАНИЧЕСКАЯ ИНДУКТИВНОСТЬ

Потенциальная величина - температура
Потоковая величина – тепловой поток
В тепловых системах физическая субстанция это количество тепла
Под тепловыми системами будем понимать технические системы, в которых происходит накопление и перенос тепловой энергии.
ТЕПЛОВЫЕ СИСТЕМЫ

ТЕПЛОВОЕ СОПРОТИВЛЕНИЕ

ТЕПЛОВАЯ ЕМКОСТЬ
Если некоторая деталь или конструкция выполнены из ма­териала с высокой теплопроводностью, то их температуру можно приближенно постоянной во всем объеме конструкции V.
В этом случае тепловое состояние конструкции в любой текущий момент времени t допустимо характеризовать лишь одним значением температуры .

ТЕПЛОВАЯ ИНДУКТИВНОСТЬ
Эмпирический закон теплопроводности Фурье предполагает, что в ответ на появление в материале с конечным коэф­фициентом теплопроводности градиента температуры мгновенно возникает тепловой поток. Это равносильно предположению, что скорость распростране­ния тепловой энергии в материале бесконечно велика. Однако, в реальном материале неизбежно некоторое запаздывание возникновения теплового потока по отношению к появлению градиента температуры. Величина такого запаздывания зависит от микромеханизма передачи тепловой энергии в материале и связана со временем обмена энергией между отдельными эле­ментами микроструктуры материала.

ГИДРАВЛИЧЕСКИЕ СИСТЕМЫ
Системы, в которых происходит перемещение несжимаемой жидкости, называются гидравлическими системами
Физическая субстанция - несжимаемая жидкость
Потенциальная величина - давление
Потоковая величина – объемный расход

ЛАМИНАРНОЕ ТЕЧЕНИЕ ЖИДКОСТИ

ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ
Гидравлическое сопротивление зависит от формы сечения трубопровода, если сечение не является круг­лым

ГИДРАВЛИЧЕСКАЯ ЕМКОСТЬ
Истечение жидкости из вертикального цилиндрического сосуда поперечным сечением площадью S через трубопровод, присоединенный к плоскому дну сосуда.

ГИДРАВЛИЧЕСКАЯ ИНДУКТИВНОСТЬ

АНАЛОГИЯ ЭЛЕМЕНТОВ МОДЕЛЕЙ МАКРОУРОВНЯ
Вывод: в различных системах можно выделить простей­шие элементы, математические модели, которые с точностью до обозначений совпа­дают с моделями идеализированного резистора, конденсатора и ка­тушки индуктивности.

АДЕКВАТНОСТЬ МОДЕЛЕЙ МАКРОУРОВНЯ
Применение математических моделей макро­уровня простейших типовых элементов для описания реальных систем вызывает неизбежные погрешности.
Одной из причин возникновения погрешностей при исполь­зовании математической модели макроуровня является пренебрежение простран­ственным распределением параметров, характеризующих свой­ства типовых элементов и протекающие в них процессы
Поэтому для выявления области адекватности моделей макро­уровня даже простых элементов (резистор, конденсатор или катушка индуктивности) требуется рассмотрение математических моделей микроуровня физических процессов протекающих в этих объектах

МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ ТИПОВЫХ ЭЛЕМЕНТОВ
Механическая
подсистема
Электрическая
подсистема
Тепловая
подсистема
Гидравлическая
подсистема
При математическом моделировании технического устрой­ства, в котором протекают процессы различной физической природы, прежде всего необходимо для каждого из таких про­цессов выделить типовые элементы, образующие од­нородную по физическим свойствам электрическую, механическую, тепловую, гидравлическую и т.п. систему.

При описании модели ма­кроуровня сложной системы, состоящей из большого числа взаимосвязанных между собой типовых элементов, необходимо оперировать эквивалентными схемами, осно­ванными на аналогиях между математическими моделями элементов, принадлежащих различным физическим системам.
Под эквивалентной схемой системы, состоящей из ти­повых элементов, понимают их условное изображение в виде двухполюсников и связей между ними
Эквивалентную схему в виде элек­трической цепи, объединяющей двухполюсники, можно считать наглядным представлением структурной математической мо­дели рассматриваемой системы.
При построении математической модели электрической системы объединяют модели входящих в эту систему типовых элементов: резисторов, конденсаторов и индуктивных катушек. Такое объединение проводят, применяя к эквивалентной схеме законы Кирхго­фа.

При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Поэтому алгебраическая сумма токов, направленных к узлу равна сумме направленных от узла.
ЗАКОНЫ КИРХГОФА
Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю

МЕХАНИЧЕСКИЕ СИСТЕМЫ
Автомобильный амортизатор
Эквивалентная схема
Типовые элементы
конденсатор
индуктивность
сопротивление
Источник
напряжения
Используем законы Кирхгофа
для формулировки модели

ИСПОЛЬЗУЕМ ЗАКОНЫ КИРХГОФА
ДЛЯ ФОРМУЛИРОВКИ МОДЕЛИ
1) Потоковая величина (скорость) одинакова во всех элементах контура
2) Внешняя потенциальная величина (сила) распределяется среди всех элементов контура

УРАВНЕНИЕ МОДЕЛИ ДВИЖЕНИЯ ПОРШНЯ АМОРТИЗАТОРА

РЕЗУЛЬТАТЫ РАСЧЕТОВ