Презентация1

ТЕОРІЯ МНОЖИН
КОМБІНАТОРИКА
Теорія множин
Комбінаторика

Елементи множини
Множина та її елементи
Порівняння множин
Поняття підмножини
Перетин множин
Об’єднання множин
Різниця множин

Поняття множини є первинним поняттям математики, якому не дається означення.
Множину можна уявити, як сукупність зібрання деяких предметів, об’єднаних за певною характеристичною ознакою.
Приклади:
множина учнів класу;
множина букв латинського алфавіту;
множина чисел, які використовують при лічбі, її називають множиною натуральних чисел N.
Множина. Її елементи

Множина зазвичай позначається будь-якою великою буквою латинського алфавіту, при заданні множини переліком елементів – елементи беруться у фігурні дужки.
B={с,ї,і,ь} – множина задана переліком елементів.
Множина, яка не має жодного елемента, називається порожньою і позначається
множина всіх натуральних чисел – літерою N;
множина всіх цілих чисел – Z;
множина всіх раціональних чисел – Q;
множина всіх ірраціональних чисел – I;
множина всіх дійсних чисел R;
множина всіх комплексних чисел C.
Для деяких множин існують спеціальні позначення:

Предмети, що утворюють множину, називаються елементами множини.
Належність елемента до множини позначається .
Неналежність елемента до множини позначається , .
Приклади:
Нехай А – множина чисел першого десятка, тоді
Нехай L – множина букв латинського алфавіту, тоді

Порівняння множин
Дві множини вважаються рівними, якщо вони складаються з одних і тих самих елементів.

Поняття підмножини
Якщо кожен елемент множини А є елементом іншої множини В, то кажуть, що А є підмножиною В і записують: , якщо при цьому допускається, що множина А включає у себе всі елементи множини В, то записують .
Таким чином:
- строгий знак;
- не строгий знак.

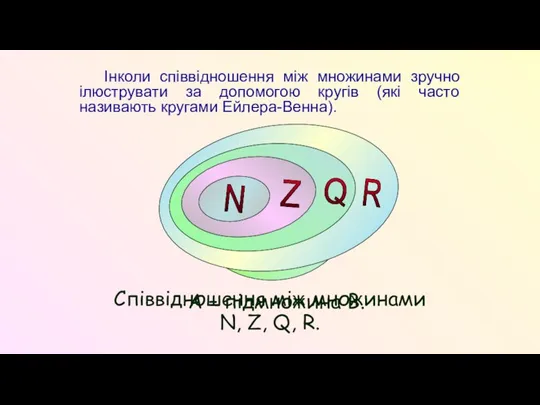
Інколи співвідношення між множинами зручно ілюструвати за допомогою кругів (які часто називають кругами Ейлера-Венна).
А – підмножина В.
Співвідношення між множинами
N, Z, Q, R.

Множини бувають скінченними і нескінченними.
Скінченна множина містить певну кількість елементів.
Наприклад:
А={1; 5; 8; 17}.
B - множина учнів в класі.
Нескінченна множина містить безліч елементів. Наприклад:
N, Z, Q, I, R, C.
B - множина точок на прямій.

Приклад:
1. А – множина всіх дільників числа 32;
В – множина всіх дільників числа 24;
А={1; 2; 3; 8; 16; 32}; B={1; 2; 3; 4; 6; 8; 12; 24};
C=A∩B;
2. А – множина всіх прямокутників;
В – множина всіх ромбів;
C=A∩B – множина всіх квадратів.
Перетин (переріз, добуток) множин
Перетином множин А і В називається множина С , що складається з усіх тих і лише тих елементів, які входять до складу кожної з даних множин А і В і є спільною частиною множин А і В.
С
Приклад:
1. А – множина всіх дільників числа 32;
В – множина всіх дільників числа 24;
А={1; 2; 3; 8; 16; 32}; B={1; 2; 3; 4; 6; 8; 12; 24};
C=A∩B; C={1; 2; 3; 8}.

Приклад:
1) А={1; 2;3; 4} B={3; 4; 5; 6}
C=AUB = {1; 2; 3; 4; 5; 6}.
2) А і B-множини точок двох трикутників зі спільною стороною.
C=AUB – множина точок опуклого многокутника.
Об’єднання (сума) множин
Об’єднанням двох множин А і В називається така множина С, яка складається з усіх елементів множин А і В і лише з них.
С