Содержание
- 2. Цель урока: Научить вычислять определённые интегралы с помощью ПЭВМ в случае, когда первообразная F для подинтегральной
- 3. План урока Приближённый метод вычисления определённого интеграла. Формула трапеции. Составление программы для вычисления площади криволинейной трапеции.
- 4. Ход урока: Приближённый метод вычисления определённого интеграла. Формула трапеции. Проблемная задача Вычислить площадь криволинейной трапеции, ограниченной
- 5. В процессе решения задачи повторить схему вычисления площади фигуры, ограниченной графиками непрерывных функций. Построить графики функций
- 6. Итак, решая поставленную задачу получили, что Возникла ситуация, когда первообразная для подинтегральной функции не выражается через
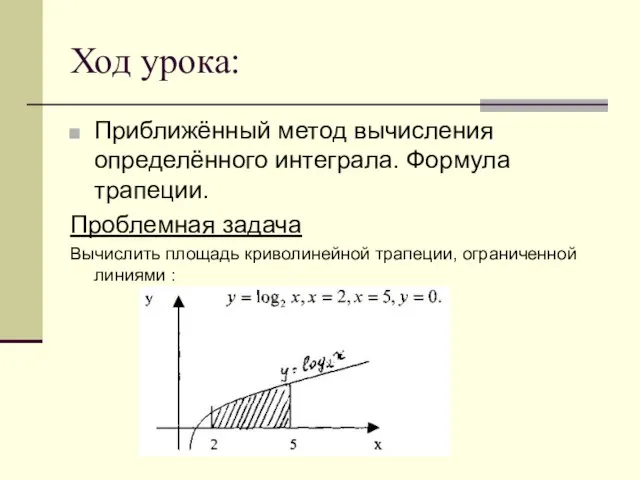
- 7. рис. 1 рис. 2 Для вычисления площади данной фигуры [а, Ь] разбивается точками на п частей
- 8. Для приближённого вычисления интеграла можно использовать формулу (1). Для приближённого вычисления интеграла можно использовать формулу (1).
- 9. Рассмотрим рис. 2. Объединение каких плоских фигур ближе к криволинейной трапеции, нежели объединение прямоугольников? Трапеций. Сумма
- 10. Точность вычисления зависит от выбора п , чем больше п, тем выше точность, но с увеличением
- 11. Если /(х) бывает, то поменять местами нижний и верхний пределы интегрирования. Это следует из того, что:
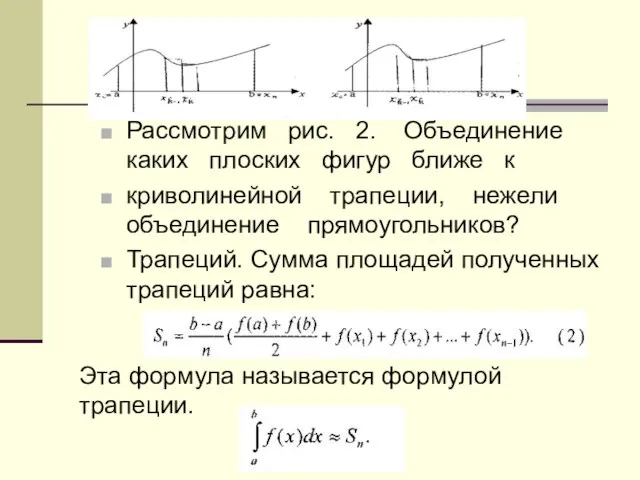
- 12. Пример. На сколько частей надо разбить отрезок [1;2], чтобы вычислить Решение.
- 14. Скачать презентацию




![рис. 1 рис. 2 Для вычисления площади данной фигуры [а, Ь] разбивается](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/439424/slide-6.jpg)



![Пример. На сколько частей надо разбить отрезок [1;2], чтобы вычислить Решение.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/439424/slide-11.jpg)
 Станковая скульптура: бюст
Станковая скульптура: бюст Отчёт директората цифрового телевидения Alma tv за период с 13 по 19 Октября 2017г
Отчёт директората цифрового телевидения Alma tv за период с 13 по 19 Октября 2017г Системный подход на благо людей и природы
Системный подход на благо людей и природы Живете
Живете Этико-правовые проблемы конца жизни человека
Этико-правовые проблемы конца жизни человека ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ПОЖАРОВ В ЖИЛЫХ И ОБЩЕСТВЕННЫХ ЗДАНИЯХ.
ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ПОЖАРОВ В ЖИЛЫХ И ОБЩЕСТВЕННЫХ ЗДАНИЯХ. УСПЕНСКИЙ СОБОР
УСПЕНСКИЙ СОБОР Опале листя: користь чи шкода
Опале листя: користь чи шкода Государственное управление в области природопользования и охраны окружающей среды
Государственное управление в области природопользования и охраны окружающей среды Магнитная гидродинамика солнечных явлений
Магнитная гидродинамика солнечных явлений Пишем проект!
Пишем проект! Этапы речевого развития
Этапы речевого развития Растения Чувашской республики
Растения Чувашской республики Эффективность стратегии диверсификации на российском рынке(эмпирическое исследование)
Эффективность стратегии диверсификации на российском рынке(эмпирическое исследование) Стресс и пути его преодоления
Стресс и пути его преодоления Интерактивные формы и методы в преподавании русского языка и литературы. Тема: Групповые формы работы на уроках русского языка и л
Интерактивные формы и методы в преподавании русского языка и литературы. Тема: Групповые формы работы на уроках русского языка и л Западный и Восточный типы культуры
Западный и Восточный типы культуры Упражнение Настроение
Упражнение Настроение Выполняй правила безопасности на дороге!
Выполняй правила безопасности на дороге! Тихонова Тамара Вячеславовна учитель истории и обществознания ГОУ лицей № 150
Тихонова Тамара Вячеславовна учитель истории и обществознания ГОУ лицей № 150 ОРКиСЭ
ОРКиСЭ Непревзойденные преимущества систем T2Red + T2Reflecta
Непревзойденные преимущества систем T2Red + T2Reflecta Модели данных
Модели данных  Модель организации внеурочной деятельности на основе краткосрочных курсов
Модель организации внеурочной деятельности на основе краткосрочных курсов История развития системы железнодорожной автоматики, применяемые на железнодорожном транспорте (АТМ) в России
История развития системы железнодорожной автоматики, применяемые на железнодорожном транспорте (АТМ) в России Высокоранговые и Низкопримативные правят миром
Высокоранговые и Низкопримативные правят миром Ртуть
Ртуть Презентация на тему: клавиатура.Авторы: Суханов Г.
Презентация на тему: клавиатура.Авторы: Суханов Г.