Причины электрического тока

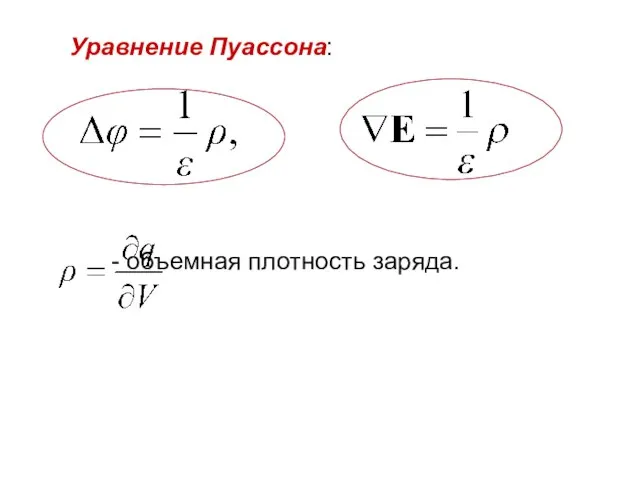
- объемная плотность заряда.
Уравнение Пуассона:

Если заряды неподвижны, то
ρ =ρ(t)=const,
Е=E(x,y,z), φ= φ(x,y,z). Поле - электростатическое.
Если есть свободные заряды, то
ρ= ρ(t), следовательно
Е=E(x,y,z,t), φ= φ(x,y,z,t).
Появляется электрический ток.
Поле перестает быть электростатическим.

Сила тока I - заряд, перенесенный через заданную поверхность S (или через поперечное сечение проводника), в единицу времени, т.е.:

Если при перемещении свободных зарядов перераспределения зарядов в пространстве не происходит, то электрическое поле – снова статическое.
Этот частный случай есть случай постоянного тока.
Ток, не изменяющийся по величине со временем – называется постоянным током
размерность силы тока в СИ:

Плотность тока
модуль вектора плотности тока численно равен отношению силы тока через элементарную площадку, перпендикулярную направлению движения носителей заряда, к ее площади

Плотность тока j связана с плотностью свободных зарядов ρ и со скоростью их движения :

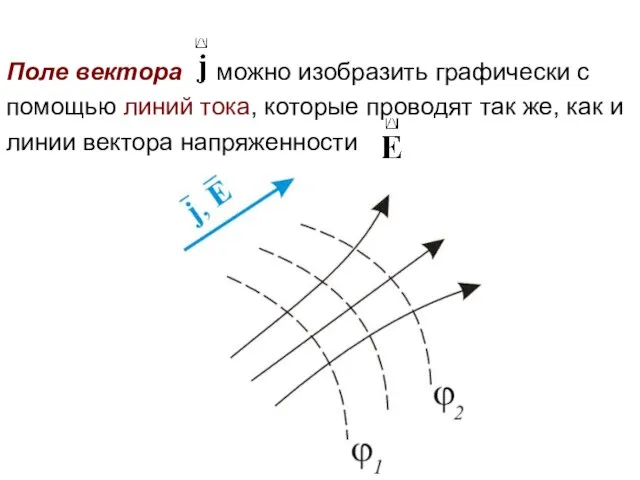
Поле вектора можно изобразить графически с
помощью линий тока, которые проводят так же, как и
линии вектора напряженности

Зная в каждой точке некоторой поверхности S можно найти силу тока через эту поверхность, как поток вектора :

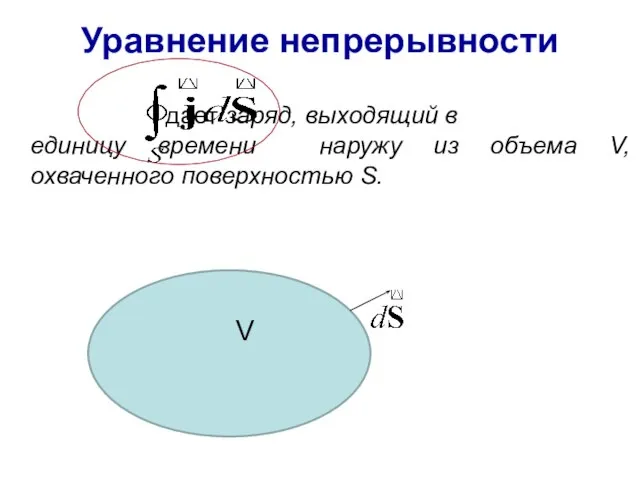
Уравнение непрерывности
дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S.
V

Плотность постоянного
электрического тока одинакова по всему
поперечному сечению S однородного
проводника.
Поэтому для постоянного тока в однородном
проводнике с поперечным сечением S сила тока:

Из этого следует, что плотности
постоянного тока в различных
поперечных сечениях 1 и 2 цепи обратно
пропорциональны площадям S1 и S2 этих
сечений :

Пусть S – замкнутая поверхность, а векторы
всюду проведены по внешним нормалям
Тогда поток вектора сквозь эту поверхность
S равен электрическому току I, идущему вовне
из области, ограниченный замкнутой
поверхностью S. Следовательно, согласно
закону сохранения электрического заряда,
суммарный электрический заряд q,
охватываемый поверхностью S, изменяется за
время на , тогда в
интегральной форме можно записать:
.

В интегральной форме можно записать:
Это соотношение называется уравнением
непрерывности. Оно является, по существу,
выражением закона сохранения электрического
заряда.
Дифференциальная форма записи уравнения непрерывности.

В случае постоянного тока, распределение зарядов в пространстве должно оставаться неизменным:
следовательно,
это уравнение непрерывности для постоянного тока (в интегральной форме).
В дифференциальной форме уравнение непрерывности для постоянного тока:

Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю.
Докажем это: т.к. для постоянного тока справедливо уравнение
отсюда
Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.

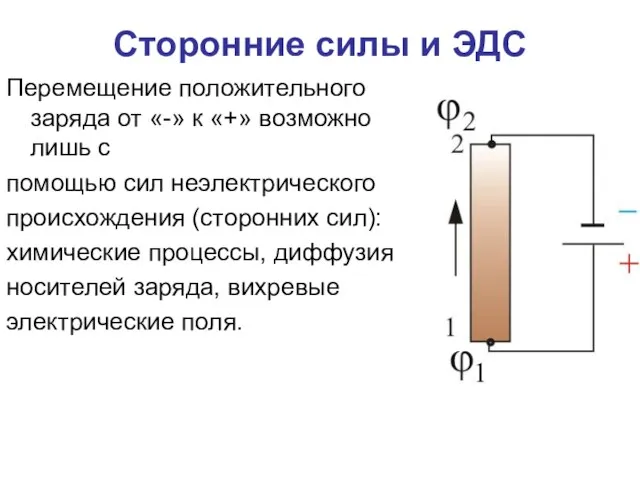
Перемещение положительного заряда от «-» к «+» возможно лишь с
помощью сил неэлектрического
происхождения (сторонних сил):
химические процессы, диффузия
носителей заряда, вихревые
электрические поля.
Сторонние силы и ЭДС

Величина, равная работе сторонних сил
по перемещению единичного положительного заряда в цепи,
называется электродвижущей силой
(Э.Д.С.), действующей в цепи:

Стороннюю силу, действующую на заряд, можно представить в виде:
– напряженность поля сторонних сил.

Работа сторонних сил на участке 1 – 2:
Тогда Э.Д.С.
Для замкнутой цепи: