Применение производной к решению задач

Цели занятия
Уточнить основные понятия и законы темы, углублённо рассмотреть конкретные вопросы во время решения задач.
Провести самостоятельное исследование по теме, перенос знаний в нестандартную ситуацию.
Проявить и развить свои способности, организовать свои цели, составить реальный план, выполнить его и оценить свои результаты.

Задание 1
1. Зная правило дифференцирования произведения двух функций, составьте формулу (u∙v∙w)΄ = …
2. Зная связь первой производной и
экстремумов, установите, как определить вид экстремума по второй производной.
(u∙v∙w)΄ = u΄∙v∙w + u∙v΄∙w + u∙v∙w΄

Задание 2
Составить алгоритм отыскания промежутков выпуклости вверх и вниз
для функции у = 2(х²)³ – 5(х²)²
1. у΄=12х5 – 20х³
2. у΄΄=60(х²)² – 60х²
3. у΄΄=0 при х=0, х=1, х=-1.
4. у΄΄> 0, функция выпукла вниз при
х ≤ -1, х ≥ 1.
5. у΄΄< 0, функция выпукла вверх при
-1 ≤ х ≤ 1.

Задание 3
Установить соответствие между предложенными графиками у=f΄(x) и формулами, задающими функцию у=f(x).
1. у= х²-1 2. у=х³- 1 3. у=(х-1)² 4. у=-х² -1
А Б В Г
Ответы: 1- Б, 2 – А, 3 – Г, 4 – В.

Работа первой группы
№ 1.
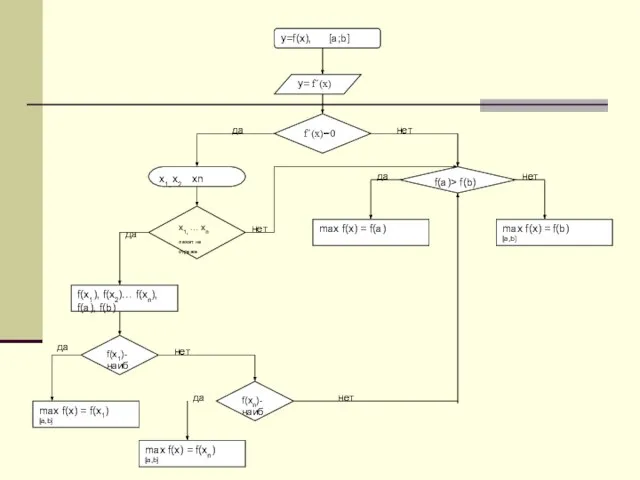
Для графика функции у=f(x): f΄(x)>0 и f(x) возрастает [-5;-2,8],[-0,4;3,5]
f΄(x)<0 и f(x) убывает [-2,8;-0,4,[3,5;5]
f΄(x)=0 и производная меняет знак с плюса на
минус при х=-2,8 и х=3,5 и х=-2,8 и х=3,5
точки максимума
f΄(x)=0 и производная меняет знак с минуса на
плюс при х=-0,4 и х=-0,4 точка минимума
Для графика функции у=f ΄΄(х): f΄(x) убывает на промежутках [-3,5;-1,5],
[0,5;1,5], [2,8;5] значит функция у=f΄΄(x)
отрицательна на этих промежутках и
обращается в нуль при х=-3,5, х=-1,5,х=0,5,
х=1,5, х=2,8
f΄(x) возрастает на промежутках [-5;-3,5],
[-1,5;0,5], [1,5;2,8] значит функция у=f΄΄(x)
положительна на этих промежутках.

Работа первой группы
№ 2.
D(у)=R, , у΄>0 при х <1 и непрерывна при х=1, значит функция возрастает на промежутке (-∞; 1], т.е. b+4≤1, b≤-3.

Работа второй группы
Напишите уравнение касательной к графику функции у=-х³-6х²+3, которая имеет наибольший угловой коэффициент.

Работа третьей группы
№ 1.
Найти наибольшее значение функции y=f(x) на отрезке [a,b].
1. Найти производную данной функции.
2. Найти критические точки.
3. Выбрать критические точки, принадлежащие заданному отрезку.
4. Найти значение функции в отобранных критических точках и концах отрезка.
5. Выбрать наибольшее значение функции.

Работа третьей группы
1. V(t)=x΄(t), V(t)=36t – 3t2
2. V΄ (t)= 36 – 6t
3. V΄ (t)=0 при t=6
4. 6 принадлежит отрезку [4,8]
5. V(4)=96 м/с, V(6)=108 м/с,
V(8)=96м/с
6. max V(t) = V(6) =108 м/с