Слайд 2Актуальность темы
1936г. Тьюринг
МТ абстрактное вычислительное устройство для мат. модели описания алгоритмов
1936г.

Черч
Любой процесс, который естественным образом мог бы быть назван процедурой, реализуем МТ. В этом смысле МТ считается эквивалентом любого ВУ
2005г. 40 лет закону Мура
Число транзисторов на одной интегральной микросхеме удваивается каждые 18 мес.
Через несколько лет размер элементарной ячейки компьютера составит 100-200 ангстрем
Новый вид носителей информации требует новых математических оснований
Слайд 3Существующие подходы
Создание “СБИС” по все более высокоскоростной технологии
Использование квантовых компьютеров для быстрого

решения сложных задач с данными большой размерности
Слайд 4Классическая МТ
MT =
Программа для пары
однозначно задает
Алгоритм работы: в любой

момент времени
если машина останавливается, иначе выбираем
и полагаем
Слайд 5Нестандартная МТ
НМТ =
Структура НМТ расширена двумя компонентами:
- множество задания

программы (где
- множество всевозможных наборов )
т.е. ,причем и
- оператор эволюции состояний и памяти
Алгоритм работы: в любой момент времени
если , то машина останавливается;
если , то происходит “естественная” эволюция
если ,то в работу машины вмешивается внешнее воздействие:
Здесь – время необходимое для перевода состояния и памяти машины из .
Слайд 6Набор моделей
Пусть – это множество НМТ (набор моделей), т.е. каждая ячейка памяти

представляет собой отдельное устройство
Изменение состояния памяти может происходить непрерывно и параллельно во всех ячейках
Такая система позволяет переосмыслить понятие “такт”, момент достижения определенного множества
Слайд 7Алгоритм решения диофантова уравнения

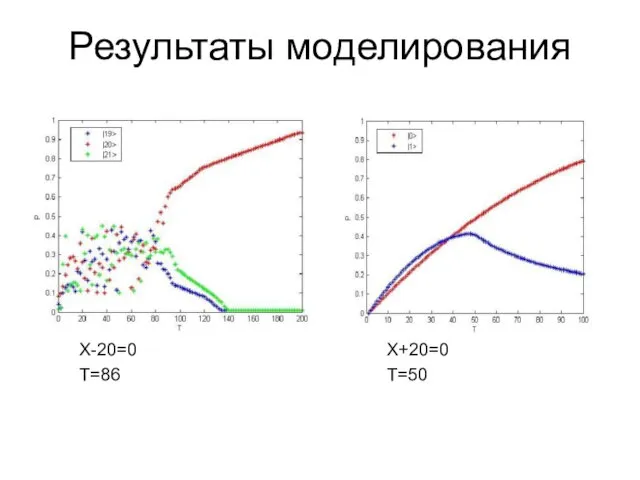
Слайд 8Результаты моделирования
X-20=0
T=86
X+20=0
T=50







 Маркетинговое планирование
Маркетинговое планирование Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г
Психологическая подготовка к всероссийской олимпиаде профессионального мастерства. 2021г ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ
ЗНАЧЕНИЕ МИРОВОГО ОКЕАНА В ЖИЗНИ ЛЮДЕЙ Ночь искусств. Театр как вид искусства
Ночь искусств. Театр как вид искусства Герои Чернушки
Герои Чернушки Фотография авангарда
Фотография авангарда Здоровье – ни с чем не сравнимая ценность. 5 класс
Здоровье – ни с чем не сравнимая ценность. 5 класс На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541
На востоке встаёт луна, На западе гаснет солнце, А ветка вишни моей цветёт. Суворова Альбина 8 класс, школа 541 Юные герои Первой мировой войны
Юные герои Первой мировой войны Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка
Методика проведения международных маркетинговых исследований Дисциплина: Международный маркетинг Преподаватель: профессор ка Презентация на тему Скульптура Древнего Рима
Презентация на тему Скульптура Древнего Рима  Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком
Переобучение, повышение квалификации женщин, находящихся в отпуске по уходу за ребенком Международно-правовое регулирование охраны труда
Международно-правовое регулирование охраны труда Бандажна проходка
Бандажна проходка Дмитрий Иванович Мендилеев
Дмитрий Иванович Мендилеев Персоналии в отечественной социальной психологии
Персоналии в отечественной социальной психологии Презентация на тему Презентации Омар Хайям
Презентация на тему Презентации Омар Хайям Тепло из недр Земли
Тепло из недр Земли Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos
Успешный опыт использования поисковой интернет- рекламы в продажах садовой техники - ООО «Садторг» (www.dom-sad.ru, www.tehnosad.ru)www.dom-sad.ruwww.tehnos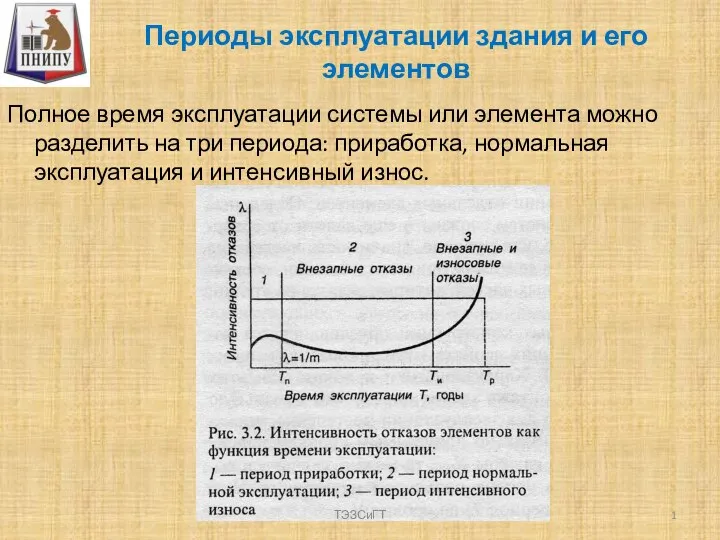 Периоды эксплуатации здания и его элементов
Периоды эксплуатации здания и его элементов Подборка телерекламы из Интернета по объекту рекламирования
Подборка телерекламы из Интернета по объекту рекламирования Когнитивные особенности младенца
Когнитивные особенности младенца Практика защиты авторских прав для произведений в интернете
Практика защиты авторских прав для произведений в интернете Презентация на тему Водные ресурсы мира (10 класс)
Презентация на тему Водные ресурсы мира (10 класс) Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Компьютерный дизайн как профессия
Компьютерный дизайн как профессия БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ)
БАСНИ- «КНИГА МУДРОСТИ САМОГО НАРОДА» (Н.В.ГОГОЛЬ) Производитель комплектующих для промышленной вентиляции
Производитель комплектующих для промышленной вентиляции