Принцип относительности Галилея

ИНСТРУКЦИЯ УПРАВЛЕНИЯ ПРОГРАММОЙ
Переход к следующему слайду, действию или ускорение действия.
Повторение предыдущего слайда, действия или отмена текущего действия.

«Результаты стрельбы будут всегда одинаковые, к какой бы стране света она ни была направлена… это произойдет потому, что так же должно получаться, будет ли Земля в движении или стоять неподвижно… Дайте движение кораблю, и притом с какой угодно скоростью, тогда (если только движение его будет равномерным, а не колеблющимся туда и сюда) вы не заметите ни малейшей разницы».
«Письма к Инголи», 1624 г.
Галилео-Галилей
(1564-1642)
Художник Оттавио Леони

Цель работы:
фронтально показать классу основные положения принципа относительности Галилея.
Актуальность работы:
непонимание учениками взаимосвязей между различными системами координат.
Новизна работы:
зрительная демонстрация материала, возможность многократного повторения основных положений теории.
Практическая значимость работы:
отработка умения и закрепление навыков решения задач по физике (части А,В,С ЕГЭ и олимпиадные задачи).

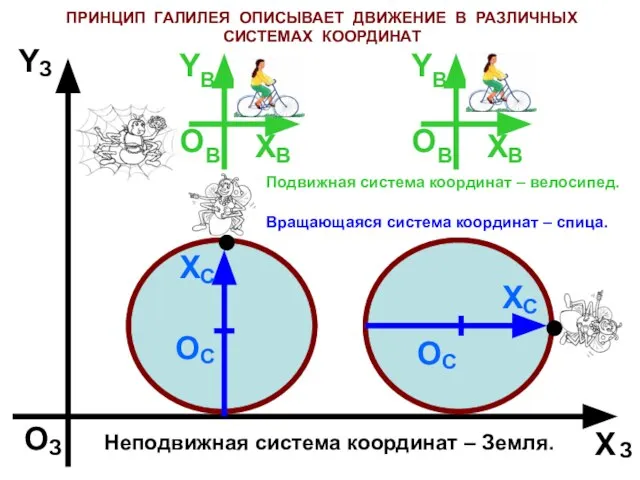
ПРИНЦИП ГАЛИЛЕЯ ОПИСЫВАЕТ ДВИЖЕНИЕ В РАЗЛИЧНЫХ СИСТЕМАХ КООРДИНАТ
O
З
Х
З
Y
З
Неподвижная система координат – Земля.
O
С
O
С
X
С
X
С
O
В
X
В
Y
B
O
В
X
В
Y
B
Подвижная система координат – велосипед.
Вращающаяся система координат – спица.

АБСОЛЮТНОГО ДВИЖЕНИЯ НЕТ!
ДВИЖЕНИЕ ВСЕГДА ОТНОСИТЕЛЬНО!
Муха спит на конце спицы колеса. По какой траектории двигается муха?
Относительно спицы муха не двигается.
В системе координат «Спица» муха покоится.
Траектория мухи в системе координат «Спица» – точка.
2) Относительно оси велосипеда муха движется по окружности. Велосипедист может увидеть три типа траектории мухи:
- окружность (если смотрит с оси велосипеда);
- эллипс (если смотрит под углом к оси);
- отрезок (если смотрит на колесо сверху).
3) Относительно Земли муха движется по циклоиде.

ВЗАИМОСВЯЗЬ
РАЗЛИЧНЫХ
СИСТЕМ
КООРДИНАТ
Х
Х
Y
Y
1
1
2
2

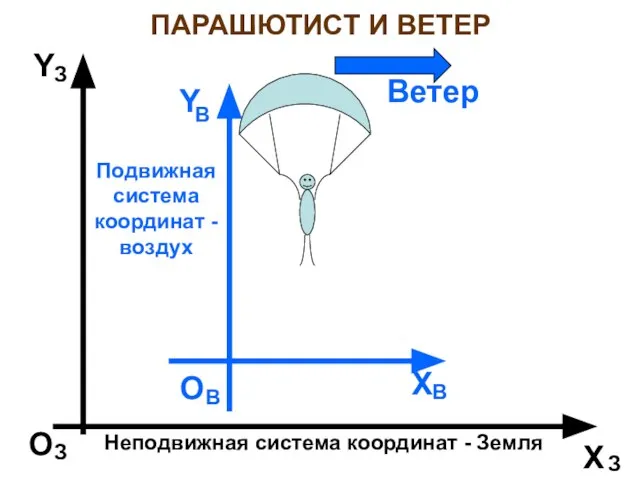
ПАРАШЮТИСТ И ВЕТЕР
Неподвижная система координат - Земля
Х
Y
O
З
З
З
O
В
X
В
Y
B
Ветер
Подвижная система координат - воздух

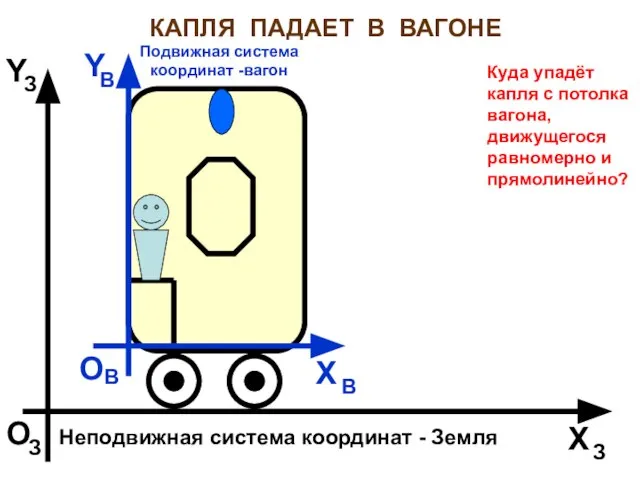
КАПЛЯ ПАДАЕТ В ВАГОНЕ
Неподвижная система координат - Земля
X
O
З
З
З
X
Y
Y
O
B
B
B
Подвижная система координат -вагон
Куда упадёт капля с потолка вагона, движущегося равномерно и прямолинейно?

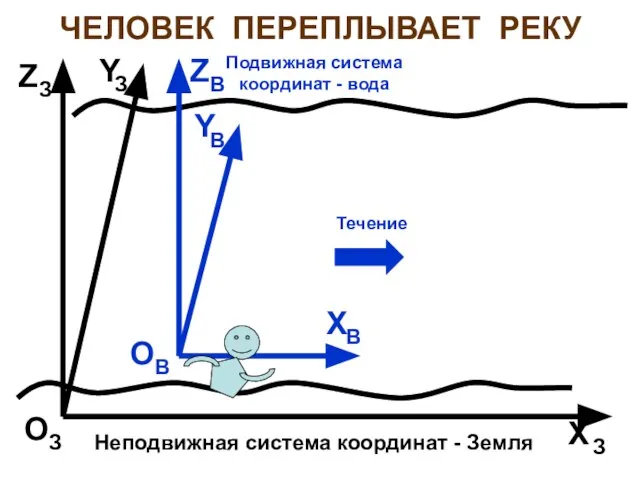
ЧЕЛОВЕК ПЕРЕПЛЫВАЕТ РЕКУ
O
X
Y
Z
B
B
B
B
Подвижная система
координат - вода
Течение
O
X
З
З
Y
З
Z
З
Неподвижная система координат - Земля

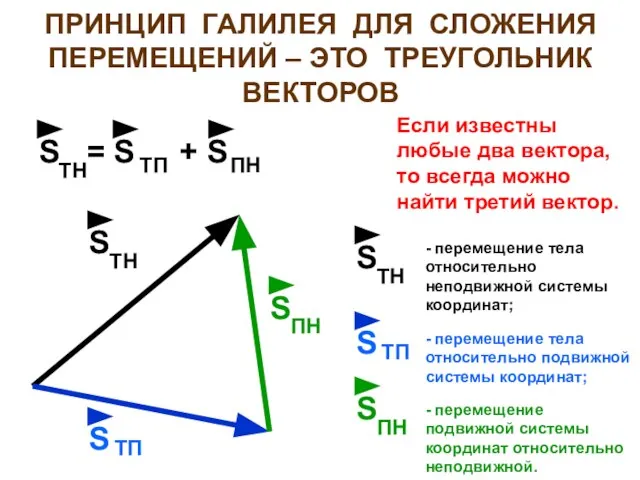
ПРИНЦИП ГАЛИЛЕЯ ДЛЯ СЛОЖЕНИЯ ПЕРЕМЕЩЕНИЙ – ЭТО ТРЕУГОЛЬНИК ВЕКТОРОВ
S = S + S
ТН
ТП
ПН
ТН
S
ТП
ПН
S
S
Если известны любые два вектора, то всегда можно найти третий вектор.
ТП
S
- перемещение тела относительно подвижной системы координат;
- перемещение тела относительно неподвижной системы координат;
- перемещение подвижной системы координат относительно неподвижной.
ПН
S
ТН
S

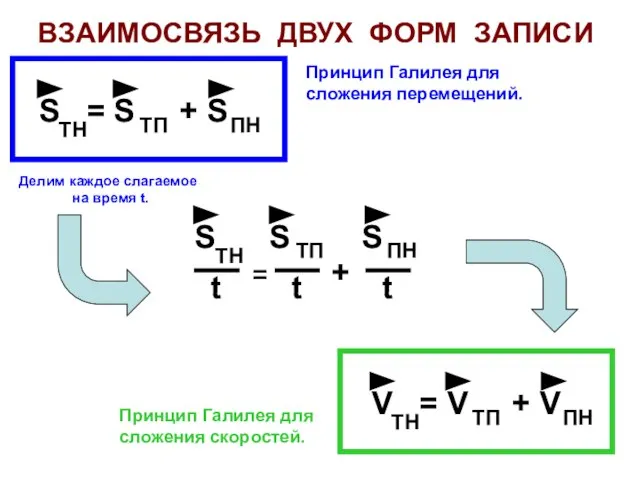
ВЗАИМОСВЯЗЬ ДВУХ ФОРМ ЗАПИСИ
S = S + S
ТН
ТП
ПН
V = V + V
ТН
ТП
ПН
S S S
ТН
ТП
ПН
=
+
t
t
t
Принцип Галилея для сложения перемещений.
Принцип Галилея для сложения скоростей.
Делим каждое слагаемое
на время t.

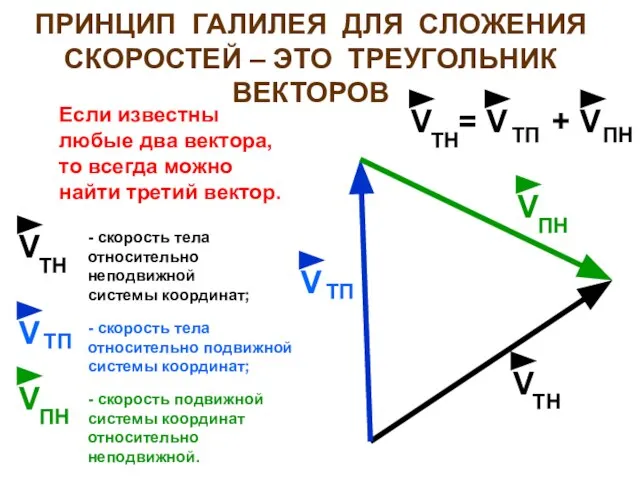
ПРИНЦИП ГАЛИЛЕЯ ДЛЯ СЛОЖЕНИЯ СКОРОСТЕЙ – ЭТО ТРЕУГОЛЬНИК ВЕКТОРОВ
ТН
V
Если известны любые два вектора, то всегда можно найти третий вектор.
ТП
V
- скорость тела относительно подвижной системы координат;
- скорость тела относительно неподвижной системы координат;
- скорость подвижной системы координат относительно неподвижной.
ПН
V
V = V + V
ТН
ТП
ПН
ТН
V
ТП
V
ПН
V

НЕ СУЩЕСТВУЕТ ПРИНЦИПА ГАЛИЛЕЯ ДЛЯ СЛОЖЕНИЯ УСКОРЕНИЙ!

БЫСТРОЕ
РЕШЕНИЕ
ЗАДАЧ
(А, В – ЕГЭ)

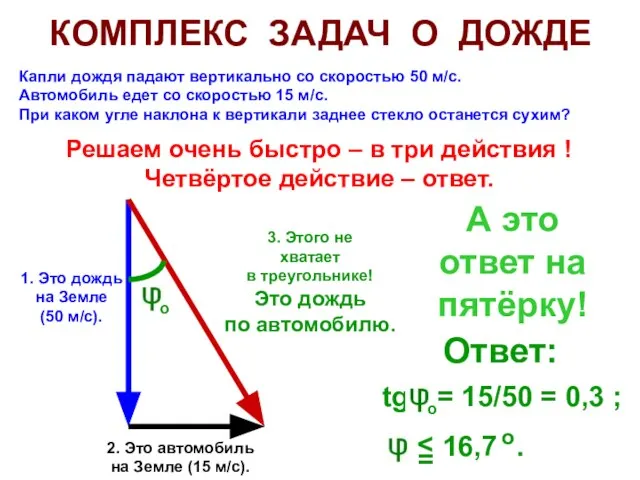
КОМПЛЕКС ЗАДАЧ О ДОЖДЕ
Капли дождя падают вертикально со скоростью 50 м/с.
Автомобиль едет со скоростью 15 м/с.
При каком угле наклона к вертикали заднее стекло останется сухим?
Решаем очень быстро – в три действия !
Четвёртое действие – ответ.
1. Это дождь
на Земле
(50 м/с).
2. Это автомобиль
на Земле (15 м/с).
3. Этого не
хватает
в треугольнике!
Это дождь
по автомобилю.
tg
= 15/50 = 0,3 ;
16,7
о
Ответ:
.
<
=
о
о
А это
ответ на
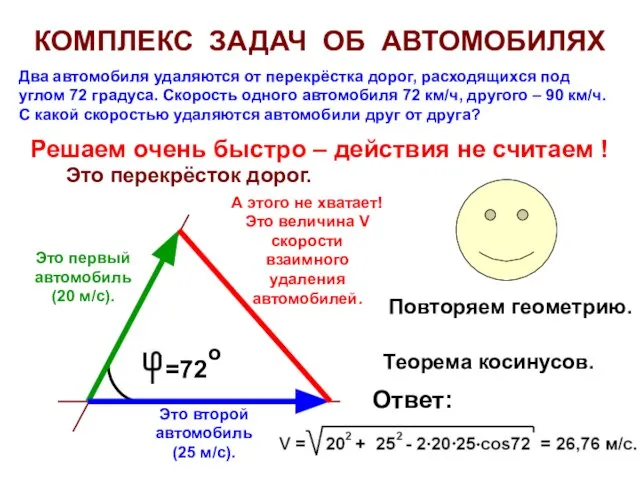
пятёрку!

КОМПЛЕКС ЗАДАЧ ОБ АВТОМОБИЛЯХ
Два автомобиля удаляются от перекрёстка дорог, расходящихся под углом 72 градуса. Скорость одного автомобиля 72 км/ч, другого – 90 км/ч. С какой скоростью удаляются автомобили друг от друга?
Решаем очень быстро – действия не считаем !
Это перекрёсток дорог.
=72
о
Это первый
автомобиль
(20 м/с).
Это второй
автомобиль
(25 м/с).
А этого не хватает!
Это величина V скорости взаимного удаления
автомобилей.
Теорема косинусов.
Ответ:
Повторяем геометрию.

ЗАДАЧИ ОБ УДАРЕ ПО МЯЧУ
Мяч летит горизонтально на футболиста со скоростью 20 м/с. Футболист ударяет абсолютно упруго по летящему навстречу мячу тяжёлым ботинком со скоростью 18 м/с. С какой скоростью полетит мяч после удара?
Ботинок «видит», что мяч летит к нему со скоростью 20+18=38 м/с.
После абсолютно упругого удара мяч отскочит от ботинка с такой же скоростью 38 м/с, но вперёд.
Ботинок добавит ещё 18 м/с. Ответ: 38+18=56 м/с.

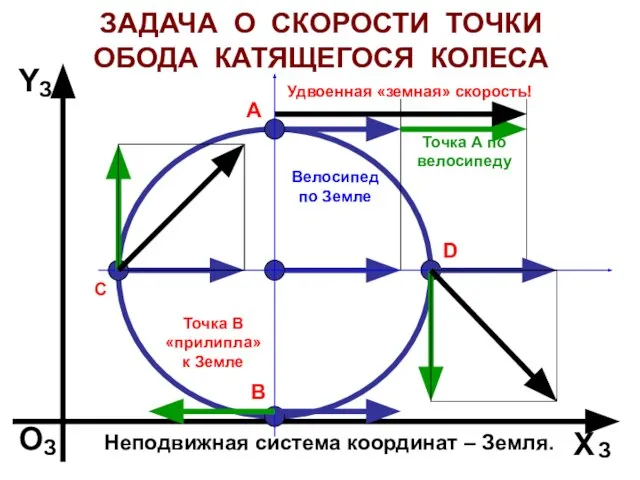
ЗАДАЧА О СКОРОСТИ ТОЧКИ ОБОДА КАТЯЩЕГОСЯ КОЛЕСА
O
З
Х
З
Y
З
Неподвижная система координат – Земля.
Удвоенная «земная» скорость!
А
Велосипед
по Земле
Точка А по
велосипеду
В
Точка В
«прилипла»
к Земле
С
D

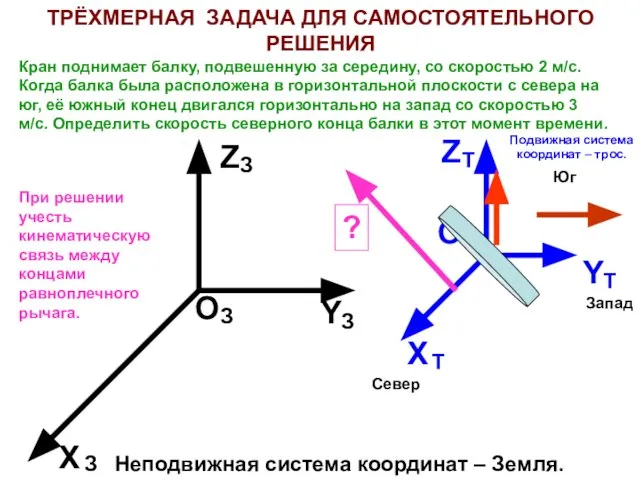
ТРЁХМЕРНАЯ ЗАДАЧА ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Кран поднимает балку, подвешенную за середину, со скоростью 2 м/с. Когда балка была расположена в горизонтальной плоскости с севера на юг, её южный конец двигался горизонтально на запад со скоростью 3 м/с. Определить скорость северного конца балки в этот момент времени.
O
З
Х
З
Y
З
Z
З
Неподвижная система координат – Земля.
O
Т
X
Т
Y
Т
Z
Т
Подвижная система
координат – трос.
Север
Юг
Запад
?
При решении учесть
кинематическую связь между концами равноплечного рычага.