Принципы управления

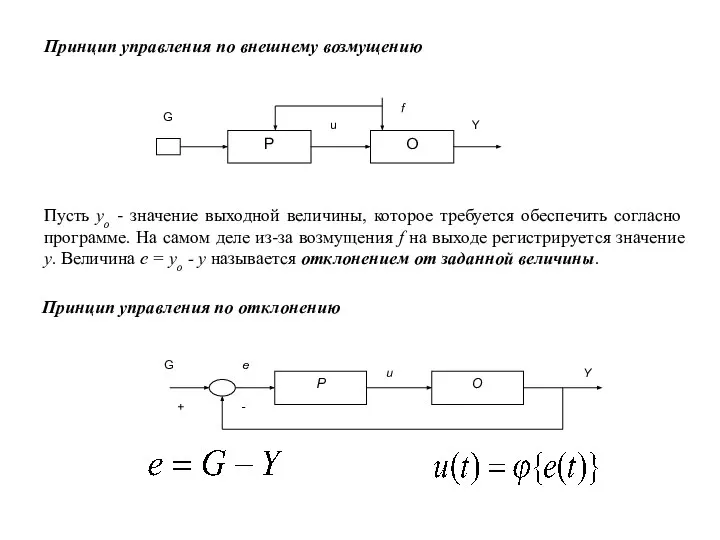
Принцип управления по внешнему возмущению
Пусть yо - значение выходной величины, которое требуется обеспечить согласно программе. На самом деле из-за возмущения f на выходе регистрируется значение y. Величина e = yо - y называется отклонением от заданной величины.
Принцип управления по отклонению

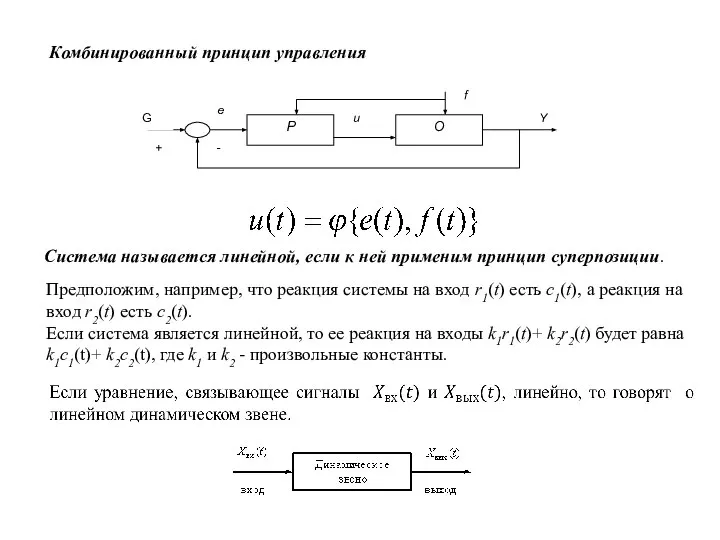
Комбинированный принцип управления
Система называется линейной, если к ней применим принцип суперпозиции.
Предположим, например, что реакция системы на вход r1(t) есть c1(t), а реакция на вход r2(t) есть c2(t).
Если система является линейной, то ее реакция на входы k1r1(t)+ k2r2(t) будет равна k1c1(t)+ k2c2(t), где k1 и k2 - произвольные константы.

Уравнение линейного динамического звена имеет следующий общий вид:
Если задать начальные условия и найти траекторию динамического движения выходной координаты, то можно записать:
С учетом оператора дифференцирования
Уравнение, которое определяет свободное движение объекта:

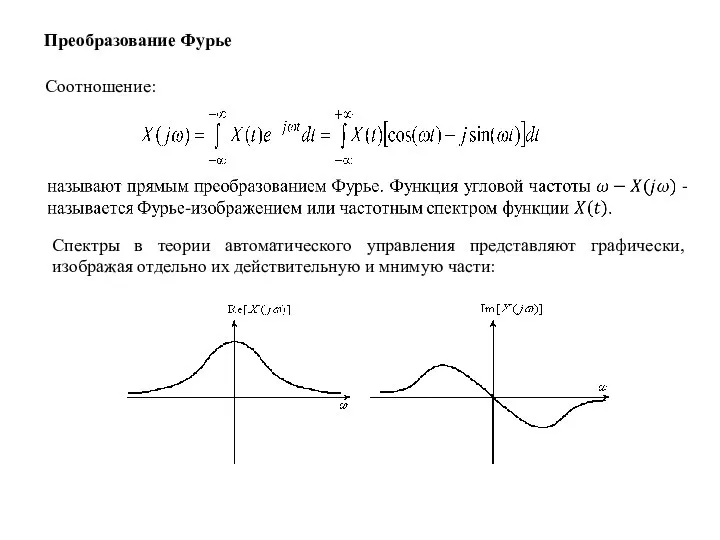
Преобразование Фурье
Соотношение:
Спектры в теории автоматического управления представляют графически, изображая отдельно их действительную и мнимую части:

Частотный спектр единичной ступенчатой функции (функция Хевисайда).
Для этой функции не выполняется требование абсолютной интегрируемости, так как
Частотный спектр дельта-функции (функция Дирака).
тождественно равна нулю повсюду, кроме точки t=0, где она стремится к бесконечности (функция описывает плотность массы 1, сосредоточенной в точке t=0, единичный импульс).

Преобразование Лапласа
Соотношение
Комплексная переменная

Изображение по Лапласу для импульсной функции
Изображение по Лапласу для единичнойфункции
Аналогично можно ввести оператор интегрирования
Фрагмент таблицы преобразования

Теорема о дифференцировании оригинала

Теорема об интегрировании оригинала
Теорема запаздывания. Для любого
справедливо соотношение
Теорема о свертке (умножении изображений)
Теорема о предельных значениях. Если
то