Слайд 2
Проблема необратимости заключается в том, как совместить обратимость по времени микроскопической динамики

с необратимостью макроскопических уравнений. Эта фундаментальная проблема рассматривалась в известных работах Больцмана, Пуанкаре, Боголюбова, Фейнмана, Ландау и других авторов, и оставалась открытой.
Недавно был предложен следующий подход к решению проблемы необратимости: предложена новая формулировка классической и квантовой механики, которая необратима по времени. Таким образом снимается противоречие между обратимость микроскопической и необратимость макроскопической динамики, поскольку обе динамики в предлагаемом подходе необратимы.
Слайд 3
Широко используемое понятие микроскопического состояния системы как точки в фазовом пространстве, а

также понятия траектории и микроскопических уравнений движения Ньютона не имеют непосредственного физического смысла, поскольку произвольные вещественные числа не наблюдаемы.
Фундаментальным уравнением микроскопической динамики в предлагаемом неньютоновском "функциональном" подходе является не уравнение Ньютона, а уравнение типа Фоккера—Планка. Показано, что уравнение Ньютона в таком подходе возникает как приближенное уравнение, описывающее динамику средних значений координат для не слишком больших промежутков времени. Вычислены поправки к уравнениям Ньютона.
Такой подход потребовал также пересмотра обычной Копенгагенской интерпретации квантовой механики.
I.V. Volovich, “Randomness in classical mechanics and quantum mechanics”, Found. Phys., 41:3 (2011), 516–528;
http://arxiv.org/pdf/0907.2445.pdf
Слайд 4
Time Irreversibility Problem
Non-Newtonian Classical Mechanics
Functional Probabilistic General Relativity
Black Hole Information

Paradox
Слайд 5Time Irreversibility Problem
The time irreversibility problem is the problem of how

to explain the irreversible behaviour
of macroscopic systems from
the time-symmetric microscopic laws:
Newton, Schrodinger Eqs –- reversible
Navier-Stokes, Boltzmann, diffusion,
Entropy increasing --- irreversible
Слайд 6Time Irreversibility Problem
Boltzmann, Maxwell, Poincar´e, Bogolyubov,
Kolmogorov, von Neumann, Landau, Prigogine,
Feynman, Kozlov,…
Poincar´e,

Landau, Prigogine, Ginzburg,
Feynman: Problem is open.
We will never solve it (Poincare)
Quantum measurement? (Landau)
Lebowitz, Goldstein, Bricmont:
Problem was solved by Boltzmann
Слайд 7Boltzmann`s answers to:
Loschmidt: statistical viewpoint
Poincare—Zermelo: extremely long
Poincare recurrence time
Coarse graining
Not

convincing…
Слайд 8Ergodicity
Boltzmann, Poincare, Hopf, Kolmogorov, Anosov, Arnold, Sinai,…:
Ergodicity, mixing,… for various important deterministic

mechanical and geometrical dynamical systems
Слайд 9Bogolyubov method
1. Newton to Liouville Eq.
Bogolyubov (BBGKI) hierarchy
2. Thermodynamic limit

(infinite number of particles)
3. The condition of weakening of initial correlations between particles in the distant past
4. Functional conjecture
5. Expansion in powers of density
Divergences.
Слайд 10Why Newton`s mechanics
can not be true?
Newton`s equations of motions use real

numbers while one can observe only rationals. (s.i.)
Classical uncertainty relations
Time irreversibility problem
Singularities in general relativity
Слайд 12Newton Equation
Phase space (q,p), Hamilton dynamical flow

Слайд 13Newton`s Classical Mechanics
Motion of a point body is described by the
trajectory

in the phase space.
Solutions of the equations of Newton or Hamilton.
Idealization: Arbitrary real numbers—non observable.
Newton`s mechanics deals with
non-observable (non-physical) quantities.
Слайд 14Real Numbers
A real number is an infinite series,
which is unphysical:

Слайд 15Try to solve these problems by developing a new, non-Newtonian mechanics.
And new,

non-Einsteinian general relativity
Слайд 16
We attempt the following solution of the irreversibility problem:
a formulation of

microscopic dynamics which is irreversible in time: Non-Newtonian Functional Approach.
Слайд 17Functional formulation of classical mechanics
Here the physical meaning is attributed not to

an individual trajectory but only to a bunch of trajectories or to the distribution function on the phase space. The fundamental equation of the microscopic dynamics in the proposed "functional" approach is not the Newton equation but the Liouville or Fokker-Planck-Kolmogorov (Langevin, Smoluchowski) equation for the distribution function of the single particle.
.
Слайд 18States and Observables in
Functional Classical Mechanics

Слайд 19States and Observables in
Functional Classical Mechanics
Not a generalized function

Слайд 20Fundamental Equation in
Functional Classical Mechanics
Looks like the Liouville equation which is used

in statistical physics
to describe a gas of particles but here we use it to describe a single particle.(moon,…)
Instead of Newton equation. No trajectories!
Слайд 21Cauchy Problem for Free Particle
Poincare, Langevin, Smolukhowsky ,
Krylov, Bogoliubov, Blokhintsev, Born,…

Слайд 25Comparison with Quantum Mechanics

Слайд 26Liouville and Newton. Characteristics

Слайд 27Corrections to Newton`s Equations
Non-Newtonian Mechanics

Слайд 28Corrections to Newton`s Equations

Слайд 29Corrections to Newton`s Equations

Слайд 31
The Newton equation in this approach appears as an approximate equation describing

the dynamics of the expected value of the position and momenta for not too large time intervals.
Corrections to the Newton equation are computed.
_____________________________
_____________________________
Слайд 32Fokker-Planck-Kolmogorov versus Newton

Слайд 33Boltzmann and Bogolyubov Equations
A method for obtaining kinetic equations from the Newton

equations of mechanics was proposed by Bogoliubov. This method has the following basic stages:
Liouville equation for the distribution function of particles in a finite volume, derive a chain of equations for the distribution functions,
pass to the infinite-volume, infinite number of particles limit,
postulate that the initial correlations between the particles were weaker in the remote past,
introduce the hypothesis that all many-particle distribution functions depend on time only via the one-particle distribution function, and use the formal expansion in power series in the density.
Non-Newtonian Functional Mechanics:
Finite volume. Two particles.
Слайд 34
Liouville equation for
two particles

Слайд 36If
satisfies the Liouville equation then
obeys to the following equation
Bogolyubov type equation

for two particles in finite volume
Слайд 37Kinetic theory for two particles
Hydrodynamics for two particles?

Слайд 38No classical determinism
Classical randomness
World is probabilistic
(classical and quantum)
Compare: Bohr, Heisenberg,
von

Neumann, Einstein,…
Слайд 40Newton`s approach: Empty space (vacuum) and point particles.
Reductionism: For physics, biology economy,

politics (freedom, liberty,…)
This approach: No empty space. Probability distribution. Collective phenomena. Subjective.
Слайд 41Fixed classical spacetime?
A fixed classical background spacetime
does not exists (Kaluza—Klein, Strings,

Branes). No black hole metric.
There is a set of classical universes and
a probability distribution
which satisfies the Liouville equation
(not Wheeler—De Witt).
Stochastic inflation?
Слайд 42Functional General Relativity
Fixed background .
Geodesics in functional mechanics
Probability distributions of

spacetimes
No fixed classical background spacetime.
No Penrose—Hawking singularity theorems
Stochastic geometry? Stochastic BH?
Слайд 43Quantum gravity.
Superstrings
The sum over manifolds is not defined.
Algorithmically unsolved problem.

Слайд 45Fixed classical spacetime?
A fixed classical background spacetime
does not exists (Kaluza—Klein, Strings,

Branes).
There is a set of classical universes and
a probability distribution
which satisfies the Liouville equation
(not Wheeler—De Witt).
Stochastic inflation?
Слайд 46Quantum gravity Bogoliubov
Correlation Functions
Use Wheeler – de Witt formulation for QG.
Density operator

of the universe on
Correlation functions
Слайд 47Factorization
Th.M. NieuwenhuizenTh.M. Nieuwenhuizen, I.V. (2005)

Слайд 49Conclusions
BH and BB information loss (irreversibility) problem
Functional formulation (non-Newtonian) of classical
mechanics:

distribution function instead of
individual trajectories. Fundamental equation:
Liouville or FPK for a single particle.
Newton equation—approximate for average values.
Corrections to Newton`s trajectories.
Stochastic general relativity. BH information problem.
QG Bogoliubov-Boltzmann equations.














































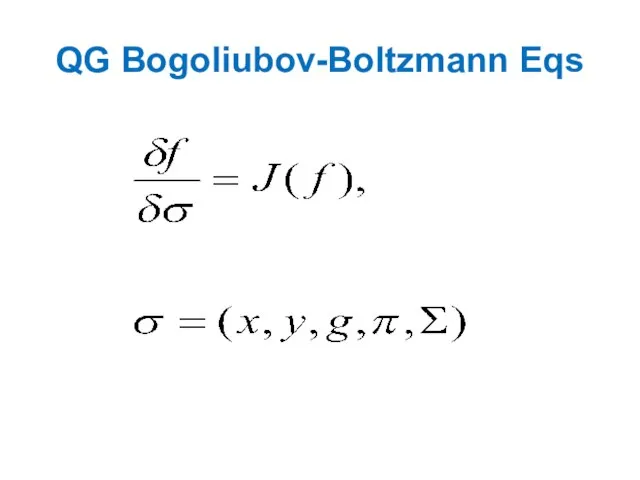


 Сожаление о старом халате.
Сожаление о старом халате. Работники культуры не бездельники ,все они
Работники культуры не бездельники ,все они Словообразование имён существительных
Словообразование имён существительных A X I O M
A X I O M Окаменевшее время Стоунхенджа
Окаменевшее время Стоунхенджа Дебаты – искусство благородного спора
Дебаты – искусство благородного спора Стулья Оримекс
Стулья Оримекс «Программируемые устройства вокруг нас»поисково-исследовательская работа
«Программируемые устройства вокруг нас»поисково-исследовательская работа ВКР: Направления развития ресурсной базы коммерческого банка
ВКР: Направления развития ресурсной базы коммерческого банка Схема передачи информации. Локальные и глобальные компьютерные сети
Схема передачи информации. Локальные и глобальные компьютерные сети Состояние отраслей машиностроения и металлообработки
Состояние отраслей машиностроения и металлообработки Презентация на тему Правовые основы охраны труда
Презентация на тему Правовые основы охраны труда риггеры на биполярных транзисторах. Генераторы линейно-изменяющегося напряжения
риггеры на биполярных транзисторах. Генераторы линейно-изменяющегося напряжения R
R Симметрия в одежде
Симметрия в одежде Роль финансов в эффективном функционировании рыночной экономики
Роль финансов в эффективном функционировании рыночной экономики  LES GENETS D’ORПрезентация организации
LES GENETS D’ORПрезентация организации День народного единства
День народного единства Мое здоровье
Мое здоровье Религиозная толерантность
Религиозная толерантность Создание эскиза театрального героя. 3 класс
Создание эскиза театрального героя. 3 класс СПИД - наиболее опасное инфекционное заболевание.
СПИД - наиболее опасное инфекционное заболевание. Прямые паруса и их бегучий такелаж шлюпа Мирный
Прямые паруса и их бегучий такелаж шлюпа Мирный Отчет по разработке Программы стратегического развития Зеленодольского муниципального района до 2020 года
Отчет по разработке Программы стратегического развития Зеленодольского муниципального района до 2020 года Постановка задачи
Постановка задачи Муниципальное образовательное учреждение средняя общеобразовательная школа № 124 Октябрьского района городского округа город Уф
Муниципальное образовательное учреждение средняя общеобразовательная школа № 124 Октябрьского района городского округа город Уф Потребительские кредиты
Потребительские кредиты Культура России в XIX в
Культура России в XIX в