Проценты в школьном курсе математики

Почему это исследование?
Мотивы выбора темы:

Практика показывает, что задачи на проценты вызывают затруднения у учащихся и очень многие окончившие школу не имеют прочных навыков обращения с процентами в повседневной жизни.
Понимание процентов и умение производить процентные расчеты в настоящее время необходимы каждому человеку: прикладное значение этой темы очень велико и затрагивает финансовую, демографическую, экологическую, социологическую и другие стороны нашей жизни.
Часто сталкиваясь с этой жизненной проблемой, я решила провести свои исследования. Работая над проектом, я исследовала:
1. учебники по математике 5-6 класс; по алгебре 7-9 классов
2.тексты ГИА для 9 класса;
3. тексты ЕГЭ для 11 класса..
Почему эта работа?

Выявить особенности учебного комплекта по математике под ред. Н.Я.Виленкина.
Провести анализ содержания данного комплекта с точки зрения изложения темы «Проценты».
Для достижения поставленных целей, проверки гипотезы и решения сформулированных выше задач были использованы следующие методы исследования:
Изучение учебно-методической и математической литературы.
Анализ школьных учебников.
Задачи данной работы:

История происхождения

Само слово «процент» происходит от лат. «pro centum», что означает в переводе «сотая доля». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
от per cento осталось «%» в XVIII в.
только o, XVII в.
аббревиатура лат.
per cento, XV в.

Индийцам проценты были известны ещё в Vв. И это очевидно, так как именно в Индии с давних пор счет велся в десятичной системе счисления
От римлян проценты перешли к другим народам Европы.
В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский ученый Симон Стевин. Он в 1584г. впервые опубликовал таблицу процентов.
Симон Стевин

Что такое процент?
Процент -
- это одна сотая часть от числа.
Процент записывается с помощью знака %.

«Работать за проценты» - работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.
«На все сто процентов» - полностью.
«Процентщик» - человек,
дающий деньги под большие
проценты, ростовщик.
Употребление процента в разговорной речи

Чтобы перевести проценты в дробь, нужно убрать знак % и разделить на 100.
Работа с процентами
Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак %.

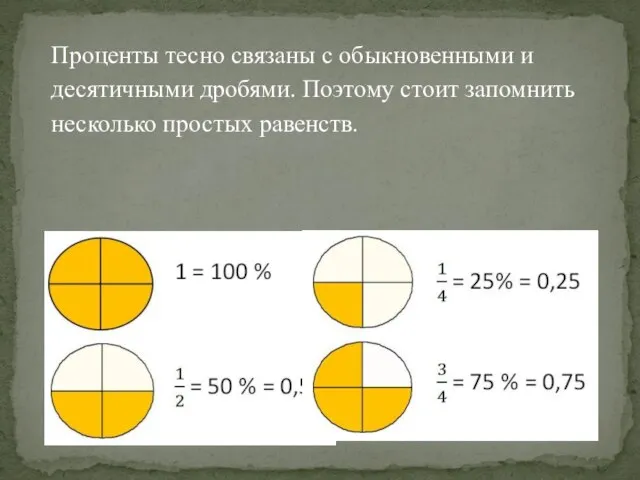
Проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств.

Проценты можно складывать и вычитать только с самими процентами.
Чтобы сложить или вычесть проценты с числами, вначале нужно проценты перевести в дробь.
2% + 38% - 35% = 40% - 35% = 5%
70% + 4 = 0,7 + 4 = 4,7
10 - (45% + 4%) = 10- 49% = 10 - 0,49 = 9,51
Сложение процентов
Умножение и деление процентов
Чтобы умножить или разделить процент на число, нужно вначале перевести процент в дробь.

I Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Чтобы найти а % от в, надо в• 0,01а.
Найдем 60 % от 500
500 x 60 % = 500 x 0,6 = 300
II Нахождение числа по его проценту
Если известно, что а % числа х равно в, то х = в : 0,01а.
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
138 составляет 23 % от всего количества.
IIIСколько процентов число составляет от другого числа
Чтобы найти, сколько процентов число составляет от другого числа, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100 %. из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?
Основные понятия, связанные с процентами:
Три основных действия:

1) Одна величина больше (меньше) другой на р%.
а) Если а больше в на р %, то а = в + 0,01рв = в(1 + 0,01р).
б) Если а меньше в на р %, то а = в - 0,01 рв = в(1 - 0,01р).
Пример. На сколько процентов надо увеличить число 60, чтобы получить 90?
Решение:
90 = 60 + 60 • 0,01р,
90 = 60(1+0,01 р)
2) Аналогично,
а) если а возросло на р %, то новое значение равно а(1 + 0,01р).
Пример. Увеличить число 80 на 20 %:
80 + 80•0,2 = 96 или 80• (1 + 0,2) = 96;
б) если а уменьшили на р %, то новое значение равно: а(1-0,01/p).
Пример. Число 96 уменьшили на 20 %:
96 - 96•0,2 = 76,8 или 96 (1 - 0.2) = 76,8.
Объединив а) и б), запишем задачу в общем виде: увеличили число а на р%, а затем полученное уменьшили на р %
а(1 + 0,01 р); а(1 + 0,01 р)(1 - 0,01 р) = а(1 -(0,01р)2) (*)
Замечание. Результат не изменится, если увеличение (уменьшение) следует за уменьшением (увеличением).
Основные типы задач на проценты

Пример 1 Швейная фабрика выпустила 1500 костюмов. Из них 40% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Решение:
1500 составляет 100%
1) 1500:100 =15 кост. составляет 1%.
2)15*40=600 кост. нового фасона
Ответ: 600 кост. нового фасона
Задача вида 1.

Пример 2: за контрольную работу по математике отметку»5» получили 15 учеников, что составляет 50% всех учеников. Сколько учеников в классе?
Решение:
Неизвестное число – 100%.
1) 15:50=0,3 учеников составляет 1%.
2) 0,3*100=30 учеников в классе.
Ответ: 30 учеников в классе.
Задача вида 2.

Пример 3: из 1800 га поля 558 га засажено картофелем. Какой процент поля засажен картофелем?
Решение:
1800 га составляют 100%.
1) 1800:100=18 га составляет 1%.
2) 558:18=31; 558 га составляют 31%.
Ответ: ; 558 га картофеля
составляют 31%.
Задача вида 3.

Задача 1. Сколько килограммов воды нужно выпарить из 0,5 тонн целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?
Задачи на концентрацию и процентное содержание
Задача 2. Кусок сплава меди цинка массой 36 кг содержит 45% меди. Какую массу меди надо добавить к этому куску, чтобы полученный новый сплав содержал 60% меди.
Задача 3.Смешали 30% -ный раствор соляной кислоты с 10% - ным раствором и получили 600 граммов 15% - ного раствора. Сколько граммов каждого раствора было взято?

Решение.
Старинным способом( Арифметика Магницкого)
30% 5 частей
15% :
10% 15 частей
5+15=20(частей)
600:20=30 (гр)- одна часть.
30*5=150 (гр) - 30%
30*15=450(гр)- 10% Ответ: 150 гр-30%,
450 гр- 10%
Задача 3.Смешали 30% -ный раствор соляной кислоты с 10% - ным раствором и получили 600 граммов 15% - ного раствора. Сколько граммов каждого раствора было взято?

Задачи из ГИА и
ЕГЭ

60 : 7,2=8,3333
Но 8, 333 сырков в магазине не продадут нужно купить либо 8, либо 9.
На 9 сырков денег не хватит, значит можно купить 8.

Решение.
1) 700 * 7 = 4900 (листов ) необходимо на 7 недель
2) 4900 : 500=9(ост 400)
в 9 пачках 4500 листов, необходимо ещё 400 листов. Значит нужно купить 10 пачек.
В пачке 500 листов бумаги формата А4. За неделю в
офисе расходуется 700 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 7 недель?

В 2008 году в городском квартале проживало 40000 человек.
В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
РЕШЕНИЕ.
В 2009 г жителей составит: 100% +8%=108%(1,08)
400*1,08=43200 (чел)
Число жителей в 2010: 100% +9%=109%(1,09)
43200*1,09=47088(чел)
ответ:47088

Теплоход рассчитан на 900 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 55 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
Решение.
925 : 55 =
925: 55= 16(ост 45)
16 шлюпок хватит на 880 человек, а на теплоходе 925, значит необходимо 17 шлюпок.

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник? Решение:
а (1+0,01х) (1-0,01х)= а(1-0,004х) обе части уравнения сократим на a.
х=20
Пусть a - стоимость акции до начала торгов в понедельник.
стоимость акции во вторник, после торгов в процессе повышения и понижения на х %, будет составлять разовое понижение на 4%,

Пусть 4a - стоимость 4-х рубашек b - стоимость куртки
4a < на 8%, т.е. составляет 0,92 части от b
4a = 0,92b /:4
a = 0,23b
Найдем процентное отношение стоимости 5 рубашек к стоимости куртки
Ответ: 5 рубашек дороже куртки 15%
Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?

S =α(1+ t p/m)
S - итоговая сумма;
α - начальная стоимость кредита;
t - срок кредита;
p - годовая процентная ставка;
m – количество дней в году;
Ежемесячный платеж :
Sкредит = S /12 t,
где Sкредит – сумма гашения кредита,
S – размер кредита,
t – срок кредитования,
Sкредит = const.
Формула Простых ПРОЦЕНТОВ

S = K ∙ (1+P∙d/D/100)ⁿ
S – сумма депозита с процентами;
K – сумма депозита (капитал);
P- годовая процентная ставка;
d – количество дней начисления процентов по привлеченному вкладу;
D – количество дней в календарном году;
n - число периодов начисления процентов;
Формула сложных процентов

Проценты творят чудеса. Зная их, бедный может стать богатым. Обманутый вчера в торговой сделке покупатель сегодня обоснованно требует процент торговой скидки. Вкладчик сбережений учится жить на проценты, грамотно размещая деньги в прибыльное дело.
В своей работе я показала применение понятия процента при решении реальных задач только из некоторых сфер жизнедеятельности человека. В ходе своего исследования я пришла к выводу, что проценты помогают нам:
Грамотно разбираться в большом потоке информации
Совершать выгодные покупки, экономя на скидках
Решать математические задачи.
Трудно назвать область, где бы не применялись проценты.
Как известно, выводы опираются на анализ. Люди не знают более удобного способа анализировать, чем процентный.
Наиболее точен и прост в применении. Его суть понятна даже ребёнку.
Применение в жизни процентных расчетов полностью рассмотреть очень сложно, так как проценты применяются во всех сферах жизнедеятельности человека. Данная тема оставляет широкое поле для дальнейших исследований.
Заключение