Проект группы экономистов

Если хотите быть богатым, научитесь не только зарабатывать, но и быть экономным.
ФРАНКЛИН Бенджамин
Как располагать средствами своими для достижения по возможности большей выгоды?

Как экономнее провести шоссе?

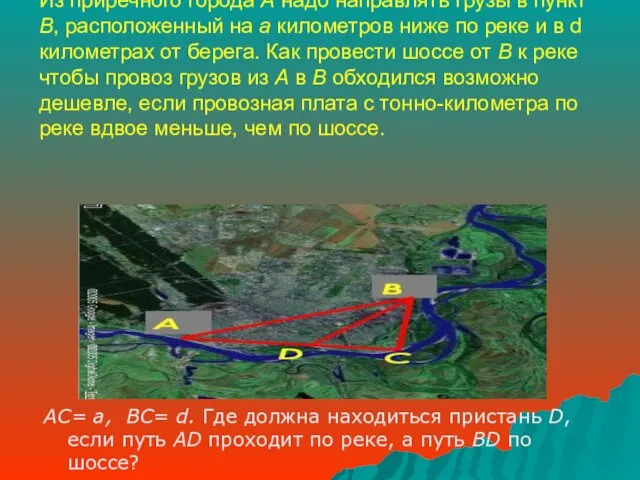
ЗАДАЧА
Из приречного города А надо направлять грузы в пункт В, расположенный на a километров ниже по реке и в d километрах от берега. Как провести шоссе от В к реке чтобы провоз грузов из А в В обходился возможно дешевле, если провозная плата с тонно-километра по реке вдвое меньше, чем по шоссе.
АС= а, ВС= d. Где должна находиться пристань D, если путь AD проходит по реке, а путь BD по шоссе?

РЕШЕНИЕ:
Так как провоз по шоссе вдвое дороже, чем по реке, то сумма m = х + 2у должна быть наименьшая.
Но ,
Решим это уравнение относительно у:
Наше уравнение принимает вид:

РЕШЕНИЕ:
Чтобы у было действительным, (m-a)2 должно быть не меньше 3d2.
Тогда ,
Из треугольника BCD имеем:
Но угол, синус которого равен , равен 60°. Значит, шоссе надо провести под углом в 60° к реке.

Если пункт расположен так, что шоссе, проведённое под углом в
к реке, пойдёт по ту сторону города А, то решение неприложимо;
в таком случае надо непосредственно связать пункт В с городом А шоссе, вовсе не пользуясь рекой для перевозки.

Некоторые практические задачи «на максимум и минимум», т. е. на разыскание наибольшего и наименьшего значений переменной величины требуют применения знаний из различных областей наук. Например для поиска наиболее оптимального режима освещения рабочего места, ведущего к повышению производительности труда, необходимо знать законы физики, геометрии, тригонометрии.

Рассмотрим аналогичную задачу:
на какой высоте над столом должно находиться пламя свечи, чтобы всего ярче освещать лежащую на столе монету?
а
х

РЕШЕНИЕ
Согласно законам оптики освещённость монеты выразится уравнением:
Так как
то освещённость равна
Это выражение достигает максимума при том же значении х, что и его квадрат, т. е.
Решив это уравнение, находим:
С учётом этого условия преобразуем уравнение к виду:

Итак, монета освещается всего ярче, когда источник света находится на высоте 0,71 расстояния от проекции источника до монеты.
Знание этого соотношения помогает при устройстве наилучшего освещения рабочего места и позволяет экономить электроэнергию и человеческие ресурсы.

Вывод.
При решении данных практических задач пригодились следующие математические знания и умения: преобразование алгебраических выражений, решение уравнений, определение синуса и косинуса острого угла прямоугольного треугольника.
Если практическую задачу можно выразить языком геометрии, причём её решение связано с решением треугольников, то необходимо знание тригонометрии.