Проецирование геометрических фигур. Поверхности. Лекция № 3

Поверхность
представляет собой трехмерный объект, образованный различными способами по различным законам.
При представлении её на плоскости проекций возникает проблема идентификации точек на поверхности. Способ идентификации напрямую зависит от способа задания поверхности на плоскости проекций.

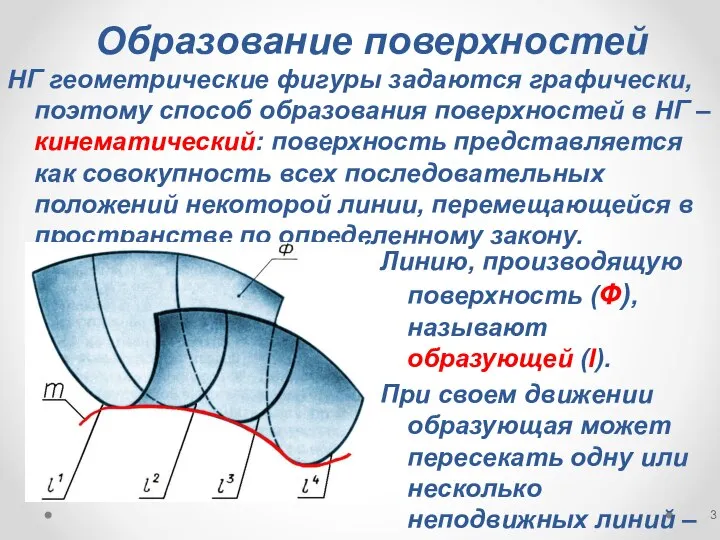
Образование поверхностей
НГ геометрические фигуры задаются графически, поэтому способ образования поверхностей в НГ – кинематический: поверхность представляется как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону.
Линию, производящую поверхность (Ф), называют образующей (l).
При своем движении образующая может пересекать одну или несколько неподвижных линий – направляющих (m)

Способы задания поверхностей
Определителем – совокупность независимых условий, однозначно определяющих поверхность (геометрические фигуры с помощью которых может быть задана поверхность, закон образования ).
Очерком – проекцией видимого контура поверхности на плоскость проекций

Определитель поверхности -совокупность условий, однозначно задающих поверхность. Φ (Г) [А]
Задание поверхности определителем
Геометрическая часть состоит из совокупности геометрических фигур (точек, линий, плоскостей и т.п.), участвующих в образовании поверхности.
Алгоритмическая часть (описательная) содержит сведения о характере изменения образующей и законе её перемещения.

Пример задания поверхности определителем
Φ (l, m, S) [S ∈ l ∩ m]

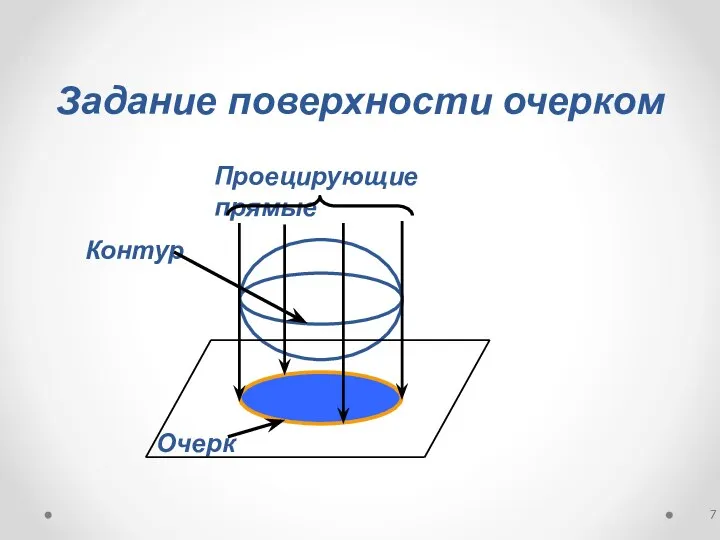
Задание поверхности очерком
Очерк
Проецирующие прямые
Контур

Классификации поверхностей
В зависимости от вида образующей
В зависимости от закона движения образующей
В зависимости от вида направляющей

Классификация поверхностей в зависимости от вида образующей
Линейчатые поверхности (образующая - прямая):
1.1. Развёртывающиеся – можно без складок и разрывов совместить с плоскостью, основной признак – наличие ребра возврата S, т.е. пространственной кривой, касательно к которой располагается образующая a во всех положениях своего перемещения по направляющей m. (например, конус, пирамида, призма, цилиндр);
1.2. Неразвёртывающиеся образуются движением прямолинейной образующей по двум или трем направляющим линиям (например, цилиндроид, коноид).

Классификация поверхностей в зависимости от вида образующей
2. Нелинейчатые поверхности (образующая - кривая) – например,.
2.1 С образующей постоянного вида - трубчатая поверхность, тор, сфера, параболоид, гиперболоид
2.2 С образующей переменного вида – циклическая поверхность.

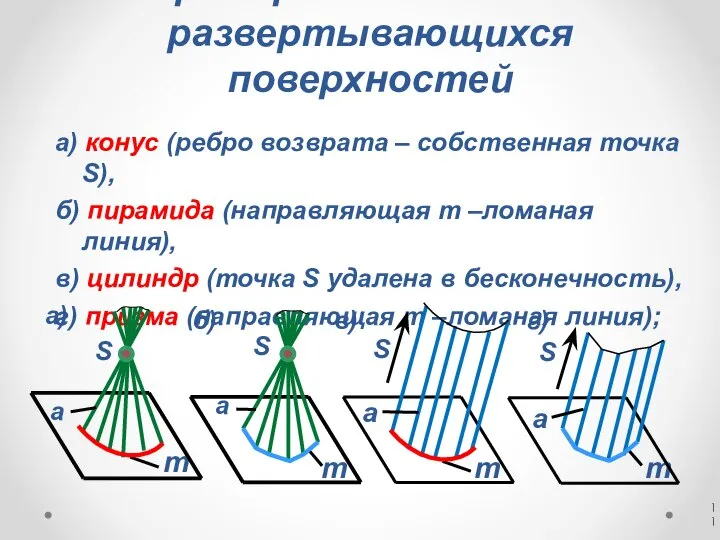
Примеры линейчатых развертывающихся поверхностей
а) конус (ребро возврата – собственная точка S),
б) пирамида (направляющая m –ломаная линия),
в) цилиндр (точка S удалена в бесконечность),
г) призма (направляющая m –ломаная линия);

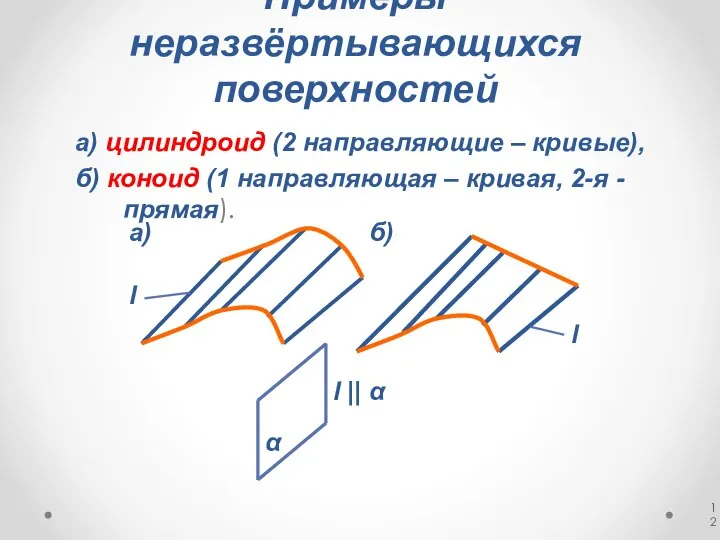
Примеры неразвёртывающихся поверхностей
а) цилиндроид (2 направляющие – кривые),
б) коноид (1 направляющая – кривая, 2-я - прямая).

Примеры нелинейчатых поверхностей
а) тор б) сфера в) трубчатая поверхность
2) с образующей переменного вида - циклическая поверхность
1) с образующей постоянного вида

Классификация поверхностей в зависимости от закона движения образующей
Поверхности вращения (образуются вращением образующей вокруг неподвижной оси) – тор, сфера, цилиндр, конус, поверхности второго порядка – эллипсоид, параболоид, гиперболоид.
Винтовые поверхности (винтовое движение образующей) - геликоид.
Поверхности с плоскостью параллелизма (с двумя направляющими линиями и направляющей плоскостью, относительно которой образующая во всех положениях остается параллельной) - прямой цилиндроид, прямой коноид, косая плоскость.
Поверхности параллельного переноса (поступательное движение образующей) - цилиндроид, коноид.

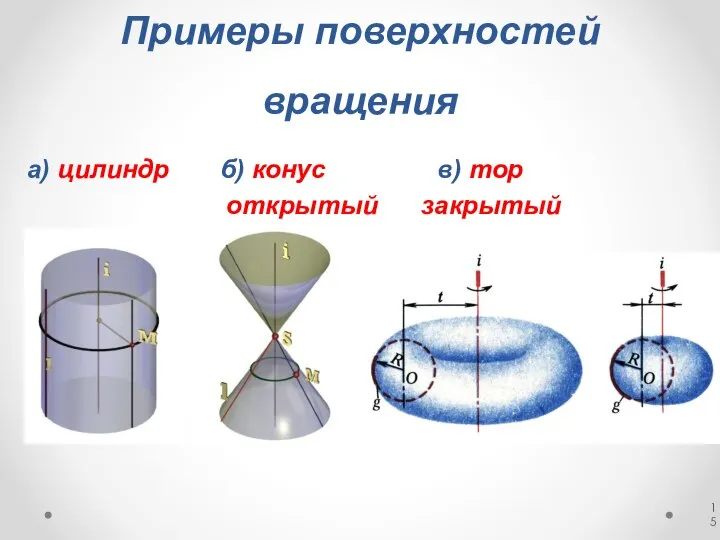
Примеры поверхностей вращения
а) цилиндр б) конус в) тор
открытый закрытый

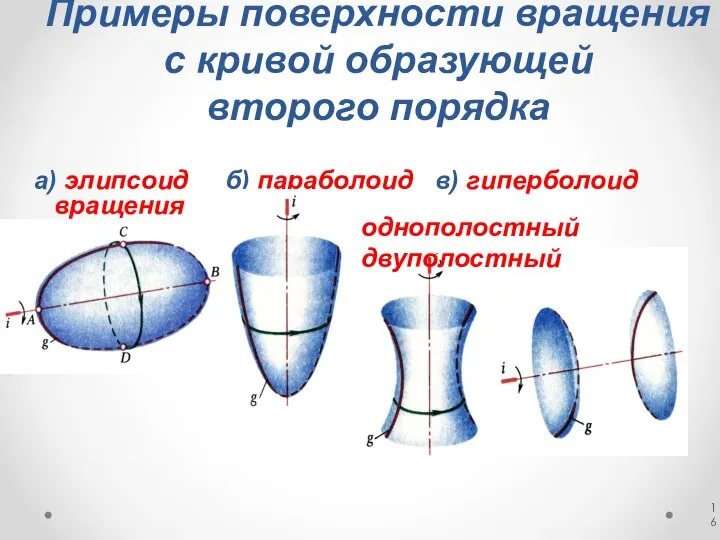
Примеры поверхности вращения с кривой образующей второго порядка
а) элипсоид б) параболоид в) гиперболоид вращения
однополостный двуполостный

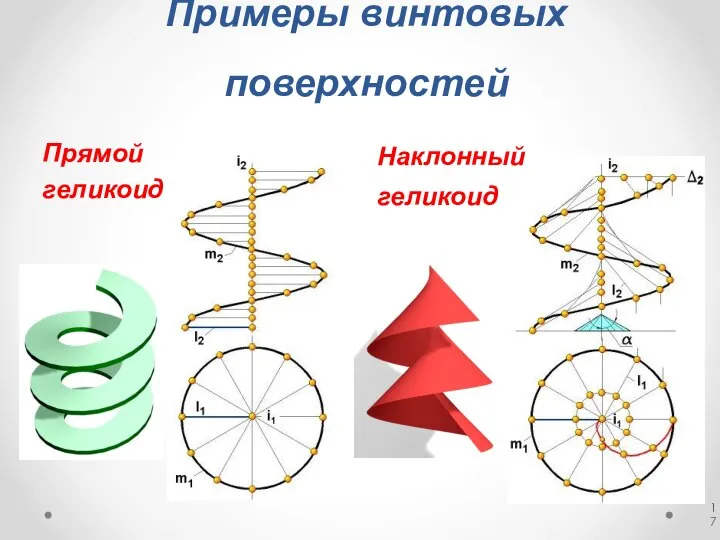
Примеры винтовых поверхностей
Прямой
геликоид
Наклонный
геликоид

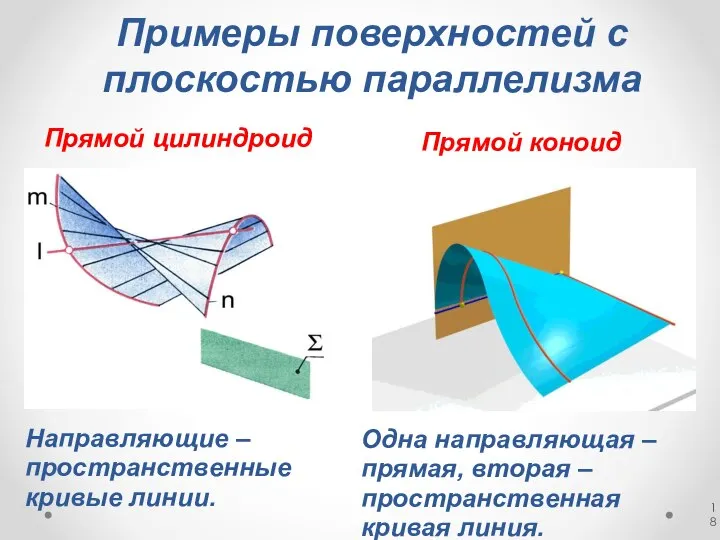
Примеры поверхностей с плоскостью параллелизма
Прямой коноид
Прямой цилиндроид
Направляющие – пространственные кривые линии.
Одна направляющая – прямая, вторая – пространственная кривая линия.

Пример поверхности параллельного переноса
Косая плоскость может быть получена путем плоскопараллельного перемещения одной из парабол как образующей по второй параболе как направляющей.

Классификация поверхностей в зависимости от вида направляющей
Кривые поверхности (направляющая – кривая линия) - цилиндроид;
Гранные поверхности (направляющая – ломаная линия) – пирамида, призма, многогранник.

Примеры кривых поверхностей
Коническая
поверхность
Косой цилиндр
с тремя
направляющими
Цилиндрическая
поверхность

Примеры гранных поверхностей

Заключение
Одну и ту же поверхность можно относить к различным классам, используя определенные для каждого класса идентификационные признаки, например, вид образующей, вид направляющей, закон движения образующей.