Угол между векторами. Скалярное произведение векторов

Ввести понятия угла между векторами и скалярного произведения векторов.
Рассмотреть формулу скалярного произведения в координатах.
Показать применение скалярного произведения векторов при решении задач.
Цели урока:

Повторение:
Какие векторы называются равными?
Как найти длину вектора по координатам его начала и конца?
Какие векторы называются коллинеарными?
или

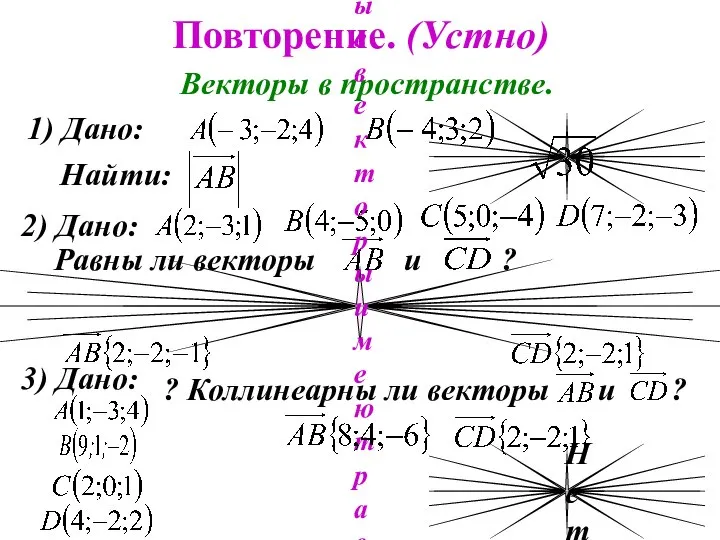
Повторение. (Устно)
Векторы в пространстве.
1) Дано:
Найти:
2) Дано:
Равны ли векторы и ?
Нет, т.к.равные векторы имеют равные
координаты.
3) Дано:
? Коллинеарны ли векторы и ?
Нет

Угол между векторами.
О
А
В
α
Если то
Если то
Если то

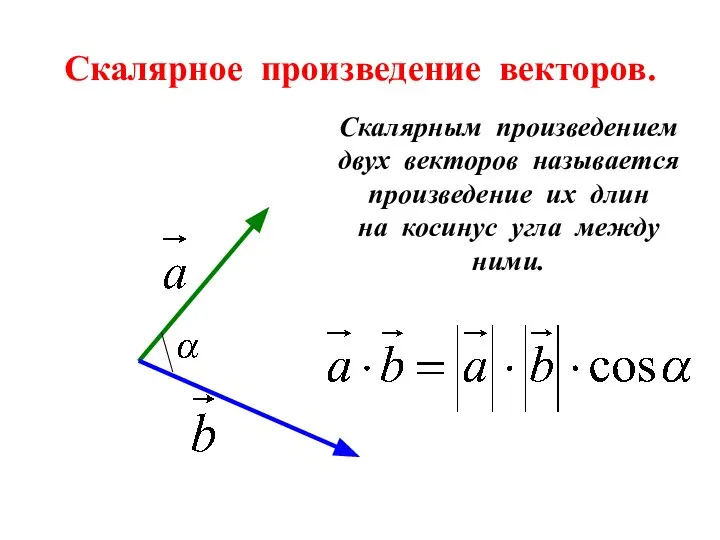
Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла между
ними.

Если , то
Если
, то
Если
, то
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Вспомним планиметрию…

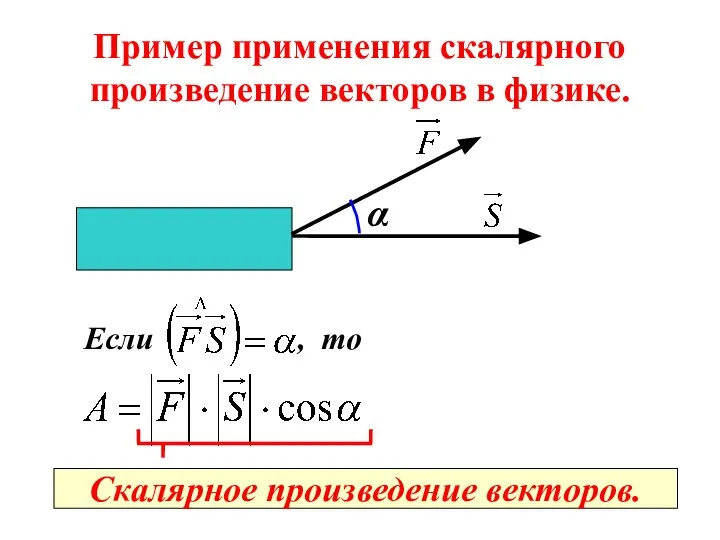
Пример применения скалярного произведение векторов в физике.
α
Если , то
Скалярное произведение векторов.

Формула скалярного произведения векторов в пространстве.
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Косинус угла между ненулевыми векторами

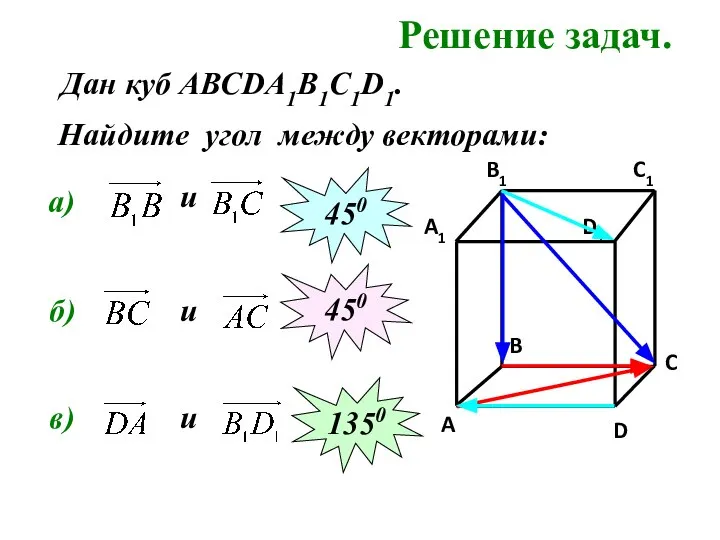
Решение задач.
Найдите угол между векторами:
а)
и
450
б)
и
450
в)
Дан куб АВСDA1B1C1D1.
и
1350

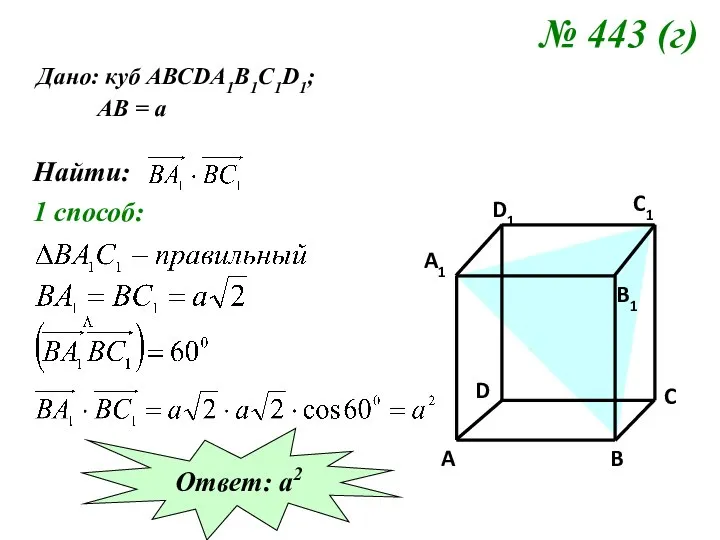
№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а
Найти:
1 способ:
Ответ: а2

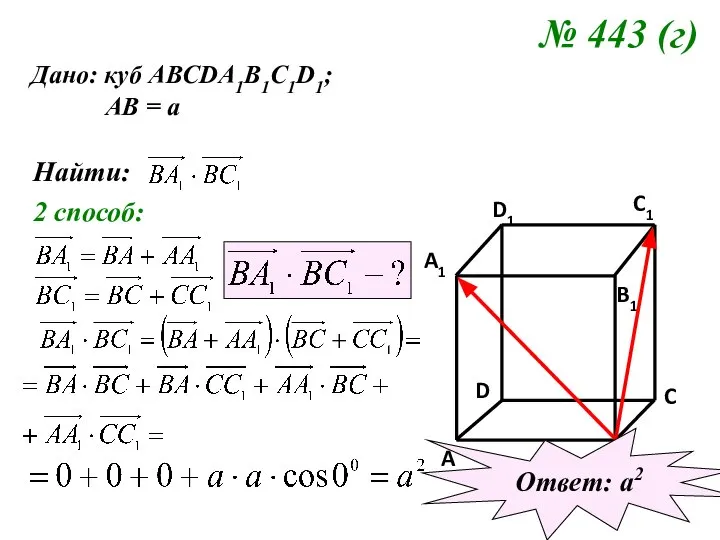
№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а
Найти:
2 способ:
Ответ: а2

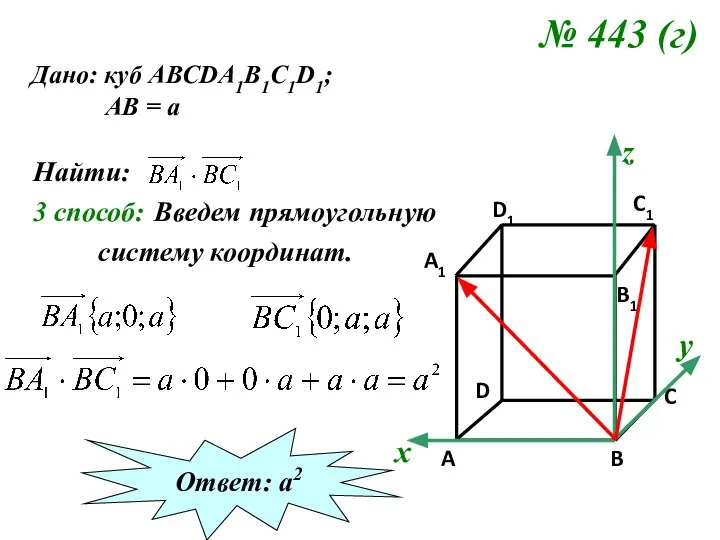
№ 443 (г)
Дано: куб АВСDA1B1C1D1;
АВ = а
Найти:
3 способ:
Введем прямоугольную
систему координат.
х
у
z
Ответ: а2

Скалярное произведение векторов.