Промежутки возрастания, убывания, знакопостоянства и нули функций

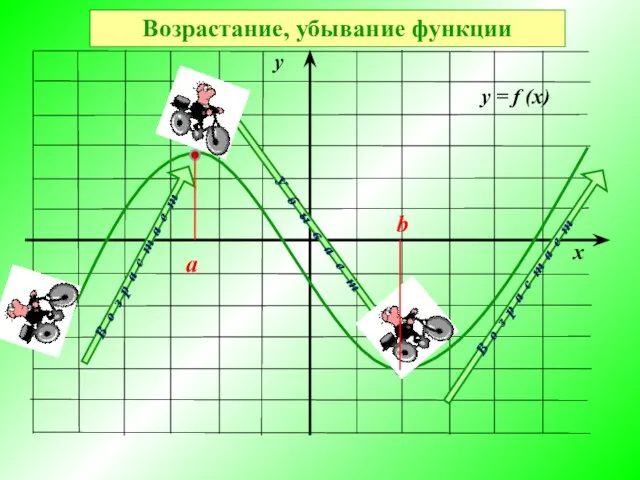
В о з р а с т а е т
У б ы в а е т
В о з р а с т а е т
Возрастание, убывание функции
a
b
у = f (x)

х₁ < x₂
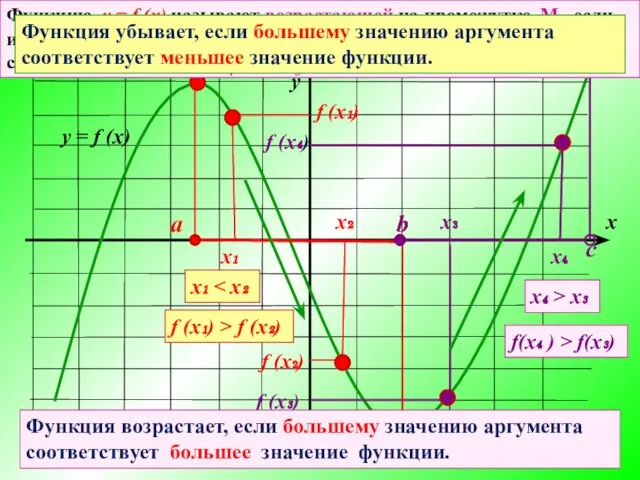
х₂
х₁
f (x₁)
f (x₂)
f (x₁) > f (x₂)
х₃
х₄
f (x₄)
f (x₃)
х₄ > x₃
f(х₄ ) > f(x₃)
a
b
c
b
Функцию y = f (x) называют убывающей на промежутке N, если из неравенства x₁ < x₂, где x₁ и x₂ - любые точки из промежутка N, следует неравенство f (x₁) > f (x₂)
Функцию y = f (x) называют возрастающей на промежутке M, если из неравенства x 3 < x 4, где x 3 и x 4 - любые точки из промежутка M, следует неравенство f (x 4 ) > f (x 3 ).
Функция возрастает, если большему значению аргумента соответствует большее значение функции.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
y = f (x)

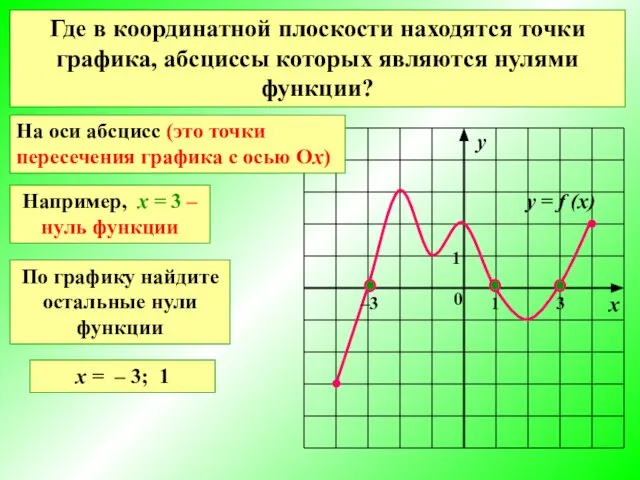
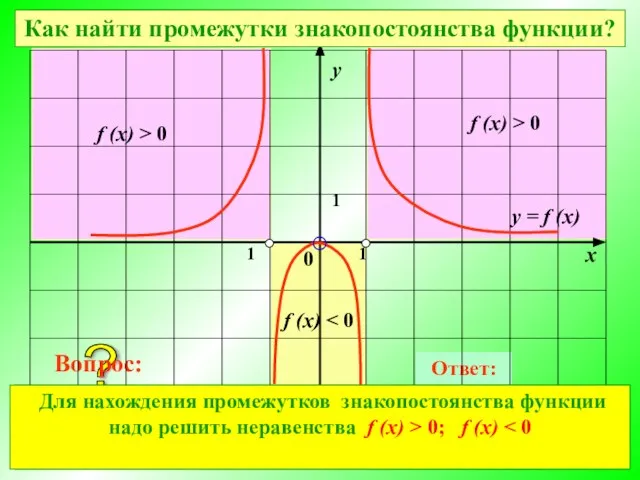
Значения аргумента, при которых значения функции равны нулю, называют нулями функции
Где в координатной плоскости находятся точки графика, абсциссы которых являются нулями функции?
На оси абсцисс (это точки пересечения графика с осью Ох)
Например, х = 3 ‒ нуль функции
3
По графику найдите остальные нули функции
‒3
х = ‒ 3; 1

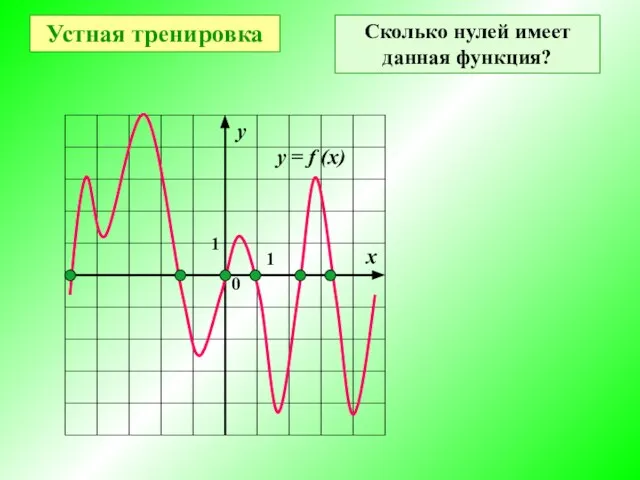
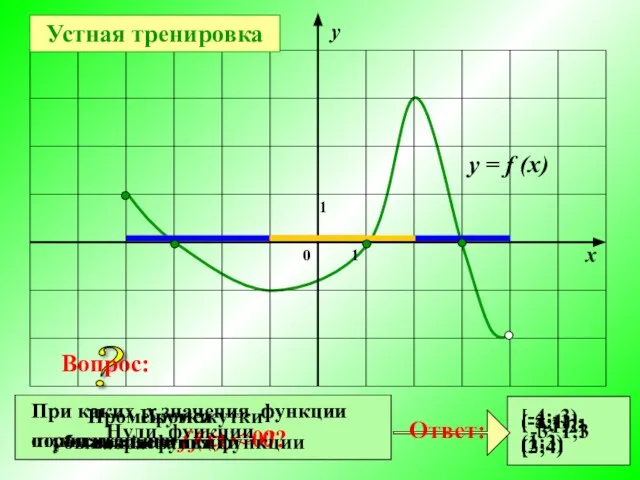
1
1
0
у
х
у = f (x)
Устная тренировка
Сколько нулей имеет
данная функция?

Как найти нули функции, заданной формулой?
Найти нули функции
По смыслу задания у = 0, тогда решаем уравнение
х ‒ 6 = 0 или х + 6 = 0, тогда
Найдите нули функций
х = 16

При каких значениях х значения
функции отрицательны?
Ответ:
При каких значениях х значения
функции положительны?
(-1;0); (0;1)
1
○
f (x) < 0
f (x) > 0
f (x) > 0
Промежутки знакопостоянства функции
Промежутки знакопостоянства функции ‒ это все значения аргумента х, при которых значения функции положительны (у > 0) или отрицательны (у < 0)
Как найти промежутки знакопостоянства функции?
Для нахождения промежутков знакопостоянства функции надо решить неравенства f (x) > 0; f (x) < 0

Какова область
определения функции?
Какова область
значений функции.
[-5;5]
[-2;4]
Назовите нули
функции.
-4;-2;0;2;4
Назовите промежутки
убывания функции
[-3;1], [1;2]
Назовите промежутки
возрастания функции.
[-5;-3], [-1;3], [3;5]
Устная тренировка

При каких х значения функции
положительны f (x) > 0?
При каких х значения функции отрицательны f (x) < 0?
[-4;-3),
(1;3)
(-3;1),
(3;4)
Нули функции
-3; 1;3
Промежутки
убывания функции
[-4;-1],
[2;4)
Промежутки
возрастания функции
[-1;2]
Устная тренировка

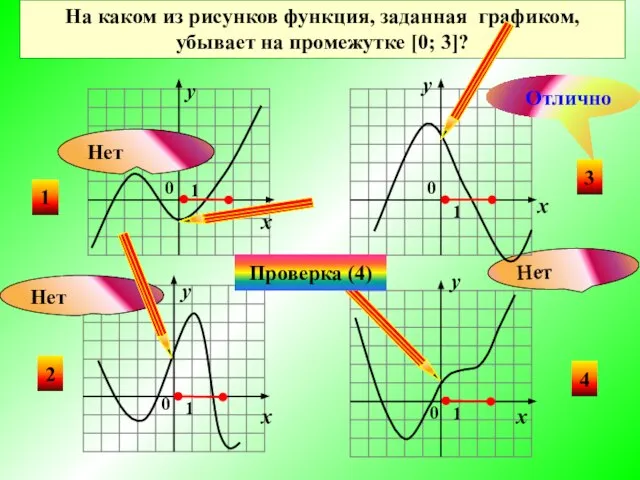
Нет
На каком из рисунков функция, заданная графиком, убывает на промежутке [0; 3]?
3
4
2
1
Нет
Отлично
Проверка (4)
Нет
x
y
0
1
0
1
0
1
0
1
x
x
x
y
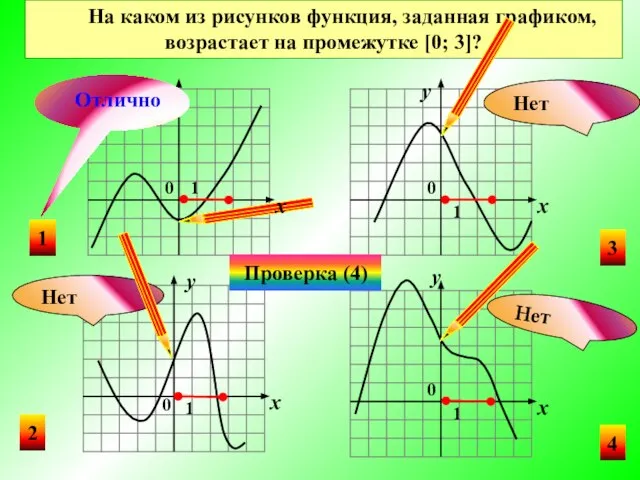
y
y

y
На каком из рисунков функция, заданная графиком,
возрастает на промежутке [0; 3]?
1
4
2
3
Нет
Отлично
Проверка (4)
Нет
Нет
x
0
1
x
0
1
x
0
1
x
0
1
y
y
y

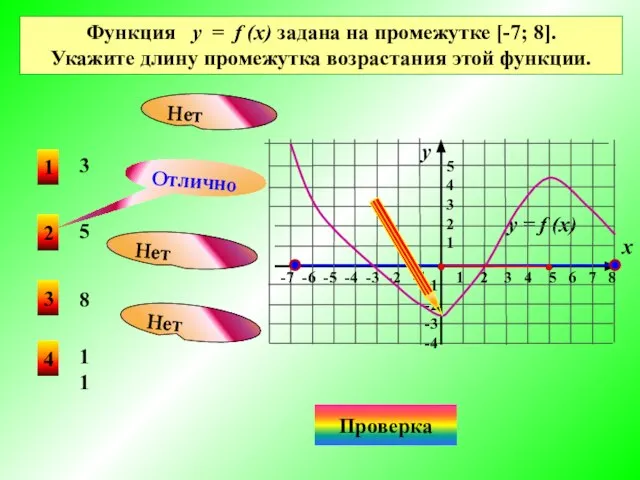
1
4
3
3
Функция у = f (x) задана на промежутке [-7; 8].
Укажите длину промежутка возрастания этой функции.
Проверка
y = f (x)
1 2 3 4 5 6 7 8
-7 -6 -5 -4 -3 -2 -1
y
x
5
4
3
2
1
-1
-2
-3
-4
2
11
8
Нет
Нет
Нет
Отлично
5

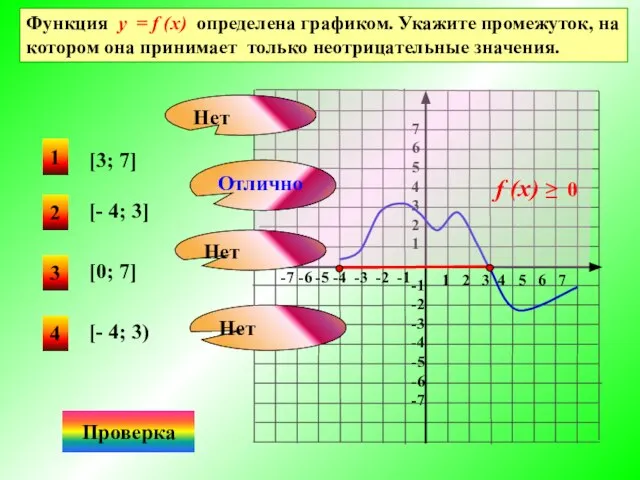
Функция у = f (x) определена графиком. Укажите промежуток, на котором она принимает только неотрицательные значения.
Проверка
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[- 4; 3]
2
1
3
4
Нет
Нет
Отлично
Нет
[3; 7]
[0; 7]
[- 4; 3)