Задача Дидоны

Содержание
Введение. Цели, задачи, актуальность.
Введение.
Миф о Дидоне.
Практическая часть.
Способы решения изопериметрической проблемы.
Первый способ.
Второй способ.
Третий способ.
Заключение.
Литература.

Цели, задачи, актуальность
Мои наблюдения показали, что кот в холодную ночь сворачивается в клубочек, дождевые капли, мыльные пузыри, Солнце, Луна, наша Земля, планеты шарообразны или почти шарообразны. Почему это происходит?
Выбранную мною тему считаю актуальной, потому что экстремальные задачи не только очень важны в математике и ее приложениях, но и красивы. Одна из таких задач – задача Дидоны, которая имеет несколько различных формулировок. Вот одна из них: среди замкнутых кривых заданной длины, найти ту, которая ограничивает фигуру наибольшей площади. Эта задача имеет различные решения.
Чтобы ответить на эти вопросы я стала изучать изопериметрическую задачу.
Изопериметрическая задача – одна из основных задач вариационного исчисления, заключающаяся в следующем: среди всех кривых данной длины найти ту, для которой некоторая величина, зависящая от кривой имеет максимальное или минимальное значение.
Объект исследования: изопериметрическая проблема.
Предмет исследования: приемы решений изопериметрической проблемы.
Цель исследования: выявить и обосновать математические средства для решения этой проблемы.
Задачи:
1) выявить математические средства для решения проблемы
2) решить задачи и доказать некоторые теоремы для решения проблемы

Миф о Дидоне
В римской мифологии есть легенда о Дидоне.
Согласно этой легенде, Дидона была дочерью царя Тира и женой жреца Геракла Акербаса; После того как брат Дидоны Пигмалион убил ее мужа, позарившись на его богатства, Дидона была вынуждена бежать. Захватив с собой часть сокровищ мужа, она в сопровождении многочисленных спутников отправилась на запад вдоль берегов Средиземного моря. Ей приглянулось одно место на побережье нынешнего Тунисского залива. Дидона повела переговоры с берберийским царем Ярбом о продаже земли. По условию она могла взять столько земли, сколько можно «окружить бычьей шкурой». Сделка состоялась. Тогда Дидона разрезала эту шкуру на тонкие ремни, связав их воедино, и окружила изрядный кусок земли. На этом месте была основана цитадель Карфагена Бирсу. (По-гречески «бирсу» как раз и означает «шкура».)
Так гласит легенда.

Формулировки задачи Дидоны
Среди замкнутых плоских кривых, имеющих заданную длину, найти кривую, охватывающую максимальную площадь.
Среди замкнутых плоских кривых, имеющих заданную площадь, найти кривую, имеющих минимальный периметр.

Эксперимент 1.
Диаграмма 1. Площади фигур равного периметра (50 см).

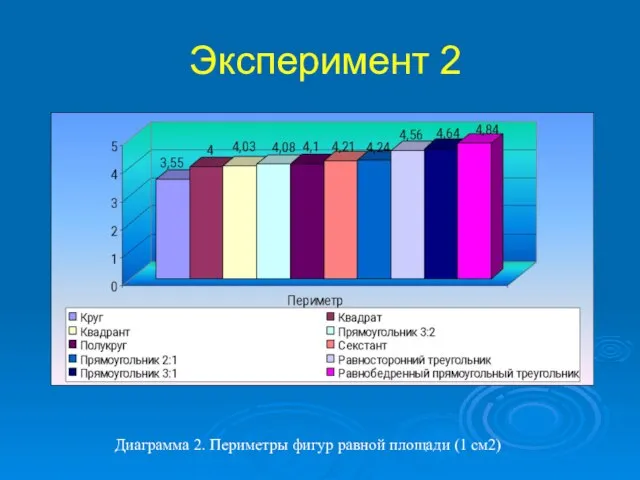
Эксперимент 2
Диаграмма 2. Периметры фигур равной площади (1 см2)

Эксперимент 3
Можно ли в листе бумаги размером с обычную страницу из тетради проделать такое отверстие, чтобы сквозь него мог пройти человек?
Если лист бумаги разрезать так, что при растяжении данной модели в результате можно получить окружность.

Эксперимент 3
Как мы это делали.

Эксперимент 3
Как мы это делали.

Первый способ
Задача 1.
Среди треугольников, у которых задана одна из сторон и сумма двух других, найдите треугольник с наибольшей площадью.

Первый способ
Задача 2. Докажите, что среди треугольников с заданным периметром наибольшую площадь имеет правильный.

Первый способ
Задача 3. Рассмотрим всевозможные n-угольники с заданными сторонами. Докажите, что среди таких многоугольников найдется многоугольник, около которого можно описать окружность, и именно этот многоугольник имеет наибольшую площадь среди рассматриваемых многоугольников.

Первый способ
Задача 4 Найти многоугольник с данным числом сторон и данным периметром, имеющий наибольшую площадь.

Первый способ
Задача5. Два правильных многоугольника, один с п, а другой с п-1 сторонами, имеют один и тот же периметр. Какой имеет боль­шую площадь?
Задача 6 Круг и правильный многоугольник имеют один и тот же периметр. Что имеет большую площадь?
Задача 7 Круг и произвольный многоугольник имеют один и тот же периметр. Что имеет большую площадь?
Задача 8 Круг и произвольная фигура имеют один и тот же пери­метр. Что имеет большую площадь?

Второй способ.
Среди всевозможных плоских замкнутых линий заданной длины найдите ту, которая ограничивает фигуру наибольшей площади.

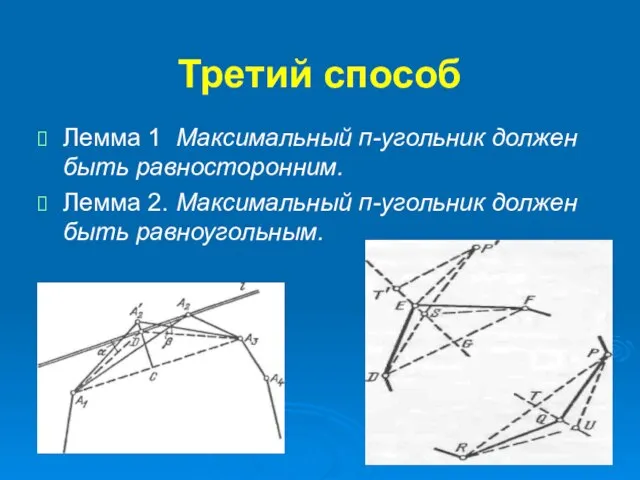
Третий способ
Лемма 1 Максимальный п-угольник должен быть равносторонним.
Лемма 2. Максимальный п-угольник должен быть равноугольным.

Третий способ
Лемма 3. Максимальный п-угольник существует. (утверждение, которое Зенодор считал само собой разумеющимся). Отсюда из лемм 1 и 2 следует
Теорема 1. Максимальный n-угольник является правиль­ным n-угольником.
Лемма 4. Для любой замкнутой плоской кривой длины Р*. охватывающей площадь S* и для любого ε > 0 можно найти некоторый п-угольник, периметр Р и площадь S которого удов­летворяют неравенствам
|Р-Р*|≤ε, |S-S*|≤ε

Обобщение и вывод
Изучив изопериметрическую теорему на плоскости можно доказать изопериметрическую теорему в пространстве: «Из всех тел равного объема наименьшую поверхность имеет шар».
Изопериметрической теореме в пространстве мы склонны верить без математического доказательства. Сама природа расположена в пользу шара. Дождевые капли, мыльные пузыри, Солнце, Луна, наша Земля, планеты шарообразны или почти шарообразны.

Обобщение и вывод
Немного зная физику поверхностного натяжения, можно научиться изопериметрической теореме у мыльного пузыря. Будучи сжаты окружающей средой, они стремятся в силу сцепления образовать при неизменном объеме более толстую поверхностную пленку, или потому, что они разрешили вопрос о том, какое тело при данном объеме имеет наименьшую поверхность.
То же можно сказать про кота, который в холодную ночь сворачивается в клубочек и таким образом делает своё тело насколько возможно шарообразным. Пытаясь сохранить тепло, он уменьшает свою поверхность. Таким образом, он решает задачу о теле с данным объемом и наименьшей поверхностью, делая себя возможно более шарообразным.