Содержание
- 2. ЖИТЕЛИ : ДРОБИ Город Дробей –двухэтажный. Того жителя который живёт на первом этаже называют Знаменатель .
- 3. В городе две главные улицы. На первой улице дома в которых Знаменатель старше. А на второй
- 5. СМЕШАННЫЙ ПРОСПЕКТ На смешанном проспекте живут смешанные числа. В их домах тоже есть Числитель и Знаменатель
- 6. ОСНОВНОЕ СВОЙСТВО ДРОБИ Дробь является всего лишь записью числа. Одному и тому же числу могут соответствовать
- 7. Сравнение дробей КОГДА ОДИНАКОВЫЕ ЗНАМЕНАТЕЛИ Чтобы узнать какая дробь больше, надо сравнить их числители, а Знаменатель
- 8. В ПОМОЩЬ
- 9. догадайся!
- 10. Действия над дробями СЛОЖЕНИЕ И ВЫЧИТАНИЕ
- 11. Когда знаменатели одинаковые ... СЛОЖЕНИЕ ПРИ ОДИНАКОВЫХ ЗНАМЕНАТЕЛЯХ Чтобы сложить дроби с одинаковыми знаменателями, надо сложить
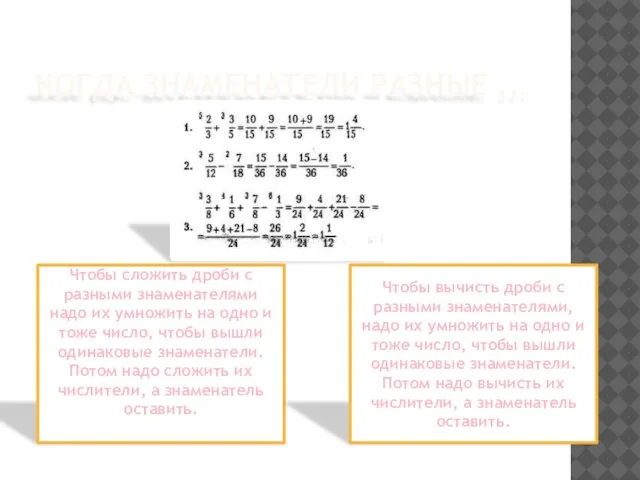
- 12. КОГДА ЗНАМЕНАТЕЛИ РАЗНЫЕ ... Чтобы сложить дроби с разными знаменателями надо их умножить на одно и
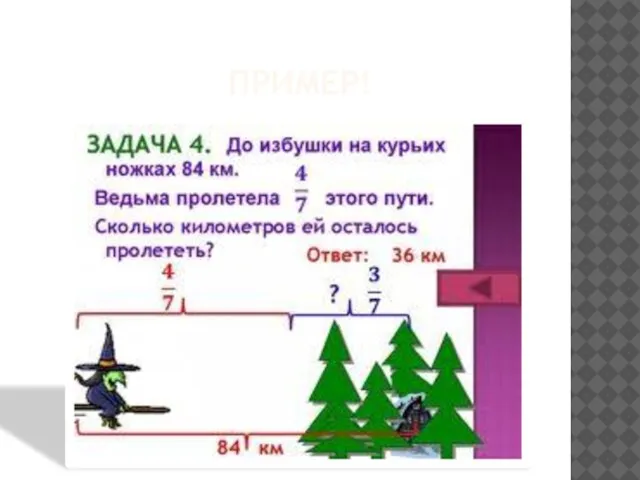
- 13. ПРИМЕР!
- 14. Реши!
- 15. Умножение
- 16. 1-ЫЙ СПОСОБ Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели. Если ответ сокращается,
- 17. 2-ОЙ СПОСОБ По второму способу сокращать надо когда производишь умножение числитель и знаменатель. Тогда выйдет несократимый
- 18. ДЕЛЕНИЕ
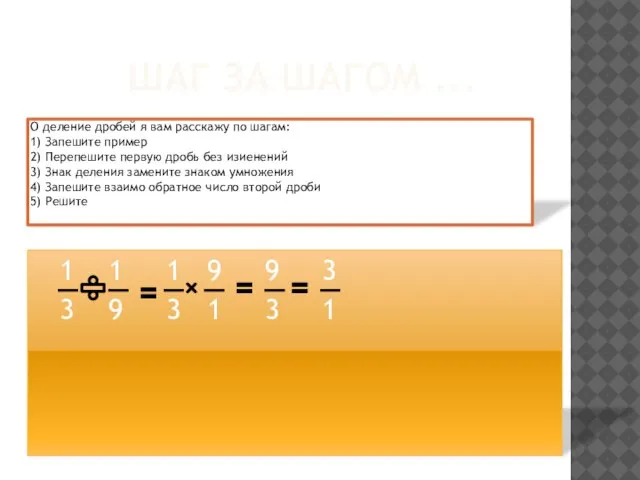
- 19. ШАГ ЗА ШАГОМ ... О деление дробей я вам расскажу по шагам: 1) Запешите пример 2)
- 20. Нахождение дроби от числа Чтобы найти дробь от числа, нужно умножить число на эту дробь.
- 21. НАХОЖДЕНИЕ ЧИСЛА ПО ЕГО ДРОБИ Чтобы найти число по его дроби, нужно разделить на эту дробь
- 25. Скачать презентацию



















 «Аспекты лидерства»
«Аспекты лидерства» ООО СПК «ЮНИТИ РЕ»
ООО СПК «ЮНИТИ РЕ» Школа 64. Традиции школы
Школа 64. Традиции школы Вводные слова и словосочетания
Вводные слова и словосочетания Презентация на тему Чем питаются животные (1 класс)
Презентация на тему Чем питаются животные (1 класс) Новогодние программы
Новогодние программы Электронный учебник на DVDи мультимедийное методическое пособие на CD для курса «Информатика и ИКТ»
Электронный учебник на DVDи мультимедийное методическое пособие на CD для курса «Информатика и ИКТ» Презентация на тему Корневище Клубень Луковица
Презентация на тему Корневище Клубень Луковица Познай Беларусь Белорусская кухня
Познай Беларусь Белорусская кухня Культура и религия
Культура и религия ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ
ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ Подготовка к региональному этапу всероссийской олимпиады школьников по обществознанию
Подготовка к региональному этапу всероссийской олимпиады школьников по обществознанию Социальные ценности и нормы
Социальные ценности и нормы Язык — душа народа!
Язык — душа народа! Сложное горячее блюдо
Сложное горячее блюдо Выбери цвет
Выбери цвет Презентация «Экология жилища» подготовлена по материалам журнала «Maxim» ученицей 9«А» класса ЦО 1685 Бариновой Дарьей Москва, 201
Презентация «Экология жилища» подготовлена по материалам журнала «Maxim» ученицей 9«А» класса ЦО 1685 Бариновой Дарьей Москва, 201 Hausratversicherung
Hausratversicherung Оценка ценных бумаг. Тема № 8
Оценка ценных бумаг. Тема № 8 Словообразование имен прилагательных (6 класс)
Словообразование имен прилагательных (6 класс) Русские народные песни
Русские народные песни Земельные ресурсы
Земельные ресурсы История, запечатленная в памятниках
История, запечатленная в памятниках Рівненський науково - виробничий центр стандартизації, метрології та сертифікації
Рівненський науково - виробничий центр стандартизації, метрології та сертифікації Кукла-мотанка. Забытая игрушка
Кукла-мотанка. Забытая игрушка Наша армия. Пограничные войска
Наша армия. Пограничные войска Урок – практикум. Подготовка и проведение.
Урок – практикум. Подготовка и проведение. Интегрированное занятиес дошкольниками «Правила безопасного перехода через дорогу»
Интегрированное занятиес дошкольниками «Правила безопасного перехода через дорогу»