Расчёт коэффициента готовности восстанавливаемой резервированной системы, состоящей из однотипных элементов

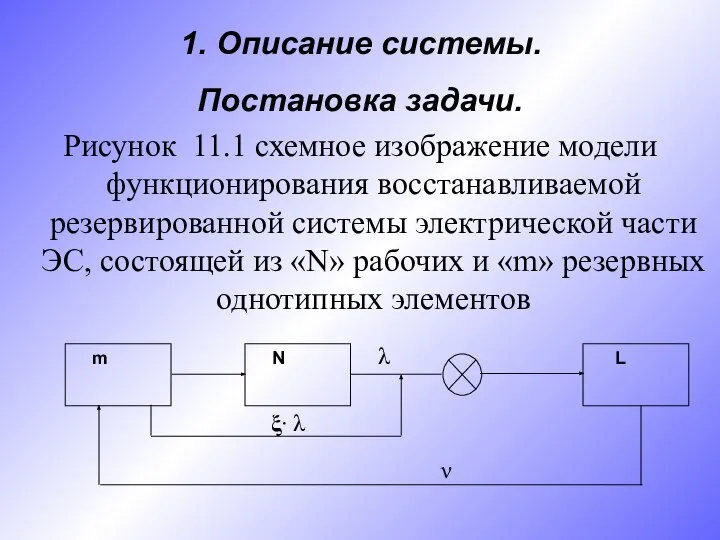
m
N
L
1. Описание системы.
Постановка задачи.
Рисунок 11.1 схемное изображение модели функционирования восстанавливаемой резервированной системы электрической части ЭС, состоящей из «N» рабочих и «m» резервных однотипных элементов
λ
ξ∙ λ
ν

m- число резервных элементов системы;
N- число рабочих элементов системы;
L- число элементов обслуживающей системы;
λ [лямбда]- интенсивность отказов элементов системы;
ν [ню]- интенсивность восстановления отказавших элементов системы
[кси]- коэффициент использования резерва.
ξ=1, если резервирование горячее; ξ=0, если резервирование холодное (отсутствуют отказы в этом состоянии);
в общем случае: 0 < = ξ < = 1
очередь на востановление

Появление отказов в системе будем рассматривать как простейший поток однородных событий, появляющихся со средней интенсивностью λ, рассматриваемой как параметр этого потока. Обслуживание рассматриваемой системы будем характеризовать показательным законом распределения времени восстановления с интенсивностью восстановления ν.
Задача поставленная перед системой, выполняется группой из N элементов. При отказе любого из элементов этой группы, он мгновенно замещается резервным, а отказавший элемент отправляется на восстановление.
Обслуживающая система состоит из L-элементов. При занятости всех обслуживающих элементов, отказавший элемент становится в очередь на восстановление.
После восстановления элемент возвращается в резерв с частотой υ.

В общем случае могут отказывать и элементы, находящиеся в резерве с частотой ξ*λ. Тогда они также направляются на восстановление в обслуживающую систему.
Следует отметить, что в данной задаче восстановление повышает надёжность системы в смысле увеличения её готовности к действию, а так же повышает вероятность безотказной работы системы в целом. Объясняется это следующим образом: чем быстрее происходит восстановление, тем более количество резервных элементов!

2. Математическое описание задачи.
Суть задачи состоит в следующем: система выходит из строя если откажут m+1 элементов.
Считаем, что система находится в состоянии Ек , когда число отказавших элементов равно К. Очевидно что в состояниях Е0, Е1,...,Еm система работоспособна. Состояние Еm+1 является состоянием отказа системы.
Состояние Еm+2 ,...,Es – cчитается невозможным, если невозможны новые отказы в отказавшей системе, где S – общее число однотипных элементов, циркулирующих в системе.
При S>N + m, некоторые из элементов находятся в нерабочем состоянии (на ремонте или в очереди на ремонт).

Предположим, что при отказе любого из элементов работающей группы, он замещается резервом. Это допущение учитывается при составлении таблицы группы технических средств для указания минимально необходимого количества технических средств в группе для обеспечения нормальной работы системы. Менее этого количества элементов опускаться нельзя, иначе наступит отказ группы и системы в целом.

Интенсивность отказа системы (из числа рабочих и резервных элементов), находящейся в состоянии Ек равна:
Nλ + (m - k) ξ λ = nk λ; (11.1)
Откуда:
nk = N + (m - k) ξ; (11.2)
Где:
ξ λ – интенсивность отказа резервного элемента;
0 < = ξ < = 1;

Интенсивность восстановления равна К ν, если количество ремонтных бригад не менее m+1 и ν, если в работе находится лишь одна бригада.
Обозначим вероятность застать систему в произвольный момент времени t в состоянии Ек через Рк(t).
Для определения Рк(t) составляется система дифференциальных уравнений конечного порядка по следующему алгоритму:
Берётся момент времени с малым приращением Δt и находится вероятность Рк(t+Δt)

В момент времени t+Δt система может находиться в состоянии Ек при следующих трёх условиях:
В момент времени t система находится в состоянии Ек и за время Δt не происходит никаких изменений с её элементами. Вероятность такого события равна:
Рк(t) * (1-nkλ Δt)*(1-k ν Δt) (11.3)
Где:
ξ – коэффициент использования резервного элемента;
nk = N + (m - k) ξ – расчётная величина;
k – число отказов из m – резервных элементов;
(1 – nk λ Δt) – вероятность того, что за время Δt в системе не возникнет ни одного отказа;
(1 - k ν Δt) – вероятность того, что не один отказавший элемент за время Δt не будет восстановлен;
k ν – интенсивность восстановления, если количество ремонтных бригад не менее: m+1, и ν – если работает лишь одна ремонтная бригада;

В момент времени t система находится в состоянии Ек-1, а за время Δt – переходит в состояние Ек. Вероятность этого события равна:
Pk-1(t) * nk-1 * λ * Δt , (11.4)
где: nk-1 * λ * Δt – вероятность отказа элемента системы;
В момент времени t система находится в состоянии Ек+1, а за время Δt – переходит в состояние Ек. Вероятность этого события равна:
Pk+1(t) * (k + 1) * ν * Δt (11.5)
Где: (k+1) – число отказавших элементов системы. Считаем, что вероятность отказа более одного элемента системы за время Δt, равна нулю!

Вероятность того, что к моменту t+Δt система перейдёт в состояние Ек любым (но только одним) из трёх вышеуказанных путей, определим по теореме сложения вероятностей несовместных событий:
Pk(t+Δt)= Рk(t)*(1-nk λ Δt)*(1-k ν Δt)+ Pk-1(t)*nk-1*λ*Δt+ Pk+1(t)*(k+1)*ν*Δt (11.6)
Перенесем влево слагаемое Рк(t) и разделим обе части уравнения на Δt. Взяв бесконечно малое приращение времени, то есть Δt →0 получим равенство:
P’k(t)= -Рк(t) * (nk λ +kν)+ Pk-1(t) * nk-1 * λ+ Pk+1(t)* (k+1) * ν (11.7)

Для определения коэффициента готовности системы в любой, произвольно выбранный момент времени t, необходимо вычислить вероятности пребывания системы в каждом из всех возможных её состояний: P0(t), P1(t),...,Pm+1(t). Указанные вероятности описываются системой дифференциальных уравнений вида:
P’0(t) = - n0 λ P0(t) + ν P1(t);
...............................................
P’ k(t) = - (nk λ + k ν) Pk(t) + nk-1 λ Pk-1(t) + (k+1) ν Pk+1(t); (11.8) .................................................................................................
P’m(t) = - (nm λ + m ν) Pm(t) + nm-1 λ Pm-1(t) + (m+1) ν Pm+1(t);
P’m+1(t)= - (m+1) ν Pm+1(t) + nm λ Pm(t);

Все события, описанные данной системой дифференциальных уравнений, являются несовместными
(не могут иметь место одновременно) и определяют возможность пребывания технической системы в любом возможном состоянии!
Следовательно сумма вероятностей системы уравнений 11.8 равна единице (полная схема событий):
= 1 (11.9)

Данная система дифференциальных уравнений может быть решена при различных начальных условиях, например: P0(0)=1; P1(0)=0; Pm+1(0)=0.
Однако, для определения коэффициента готовности системы достаточно иметь решение при t→∞ (для стационарного режима эксплуатации системы).
Согласно теореме Маркова при t→∞, Р’к=0, а
Pk(∞) = Pk = const.

С учётом сказанного, система алгебраических уравнений, определяющая коэффициент готовности технической системы, получается из системы уравнений 11.8 и имеет вид:
ν P1 = n0 λ P0;
2 ν P2 = (n1 λ + ν) P 1 – n0 λ P0;
................................................
k ν Pk = (nk-1 λ + [k-1] ν) Pk-1 – nk-2 λ Pk-2; (11.10)
.....................................................................
ν(m+1) Pm+1 = (nm λ + m ν)Pm – nm-1 λ Pm-1;
0 = (m+1) ν Pm+1 – nm λ Pm;

Из 11.10 с учётом 11.8 имеем:
(11.11)
Где: P0 – вероятность безотказной, работы системы: k=0;
(11.12)

Определим коэффициент готовности, как вероятность застать в любой момент времени неработоспособными не более m элементов.
(11.13)
Здесь: - коэффициент неисправности системы;
N-1= 1.

В заключение, проиллюстрируем зависимость функции готовности π(t) от значения коэффициента неисправности ρ:
Из анализа рисунка можно сделать вывод, что при увеличении ρ надежность системы снижается (в плане ее готовности к действию).
Вывод: При увеличении ρ коэффициент готовности системы уменьшается.

Рассмотрим некоторые частные случаи:
Случай 1. Резервирование горячее (рабочие и резервные элементы находятся в одинаковых условиях). Количество ремонтных бригад: m+1; очередь на ремонт отсутствует.
В этом случае: ξ = 1; m = S-k; где: S = N+m; 0 <= k < m + 1.

Используя формулы 11.12 и 11.11 получим:
, (11.14)
где: - число сочетаний из S по k, можно определить по формуле:

Таким образом в этом случае коэффициент готовности можно вычислить по формуле:
(11.15)

Случай 2. Если общее число однотипных элементов, которые циркулируют в рассматриваемой системе: S = > N+m и они одинаково могут отказывать в рабочем, нерабочем и резервном состояниях, то суммирование в знаменателе выражения 11.13 распространяется на все
S – элементов и коэффициент готовности системы определяется выражением:
(11.16)

Случай 3. Резервирование горячее, но работает лишь одна бригада и возможна очередь на ремонт. В этом случае коэффициенты ν в системе уравнений 11.10 везде равны единице, а ξ = 1; nk = S – k;
По формулам 11.10 и 11.11 находим:
(11.17)

Коэффициент готовности системы равен:
(11.18)

Случай 4. Резервирование холодное, работают m +1 (или S) ремонтных бригад (очередь на ремонт отсутствует). В этом случае: ξ = 0; nk = N;
Если отказы в нерабочем состоянии не появляются, то коэффициент готовности системы равен:
(11.19)

Если же элементы отказывают и в неработоспособном состоянии, то до отказов системы (до m+1 – го отказа), отказы появляются из числа N – элементов, а после этого – из числа S-k – элементов, где k (число отказов) изменяется от m+1 до S. В этом случае:
(11.20)

Случай 5. Резервирование холодное, работает одна ремонтная бригада.
В этом случае: ξ = 0; nk = N;
При отсутствии отказов в нерабочем состоянии, коэффициент готовности системы равен:
(11.21)

в случае отказов и в нерабочем состоянии коэффициент готовности системы равен:
(11.22)
Для закрепления теоретического материала предлагается самостоятельно рассмотреть количественный пример.
Исходные данные для расчета:
Пусть система состоит из двух рабочих (N=2) и двух резервных ( m=2) элементов с параметрами λ= 0.1 1/ч, υ = 1 1/ч, ρ = λ/ υ = 0.1. Расчет произвести для варианта горячего резервирования: ξ =1 и при условии, что ограничения на ремонт отсутствуют.

Выводы: Для расчета коэффициента готовности системы можно использовать формулы, позволяющие производить расчеты без решения систем дифференциальных и алгебраических уравнений, что значительно упрощает практические инженерные расчеты.